Комплексные числа. Курсовая работа Комплексные числа. Решение задач по теме Комплексные числа в углубленном курсе алгебры и начал математического анализа
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
2.3. Действия с комплексными числами в тригонометрической формеЗадача 1. Представьте комплексные числа в тригонометрической форме: а) 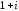 ; б) ; б) 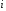 ; в) ; в) 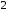 ; г) ; г) 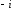 ; д) ; д) 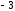 ; е) ; е) 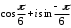 ; ж) ; ж) 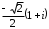 . .Решение: Комплексное число в тригонометрической форме представляет в следующей форме 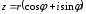 , тогда: , тогда: а) Так как 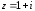 ,то ,то 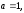 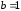 . . Тогда 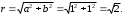 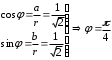 , ,Таким образом, 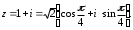 б) 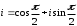 , где , где 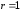 , , 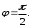 в) 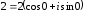 , где , где 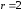 , , 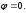 г) 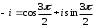 , где , где 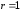 , , 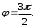 д) 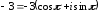 , где , где 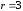 , , 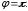 е) Так как cos функция четная, то 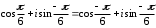 . . ж) Модуль комплексного числа равен 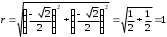 , а , а 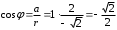 , то , то 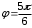 . .Таким образом, 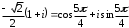 Ответ: 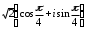 ; ; 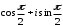 4; 4; 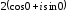 ; ; 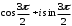 ; ; 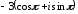 ; ; 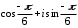 ; ; 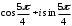 . .Задача 2. Представьте комплексное число в тригонометрической форме 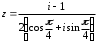 . .Решение: Предположим что 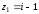 , а , а 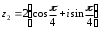 . .Тогда 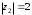 , , 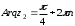 , , 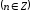 . .Поскольку 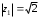 и и 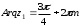 , , 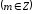 , то , то 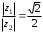 , а , а 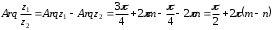 . .Таким образом, 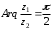 , поэтому , поэтому 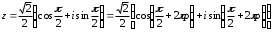 , где , где 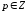 . .Ответ: 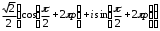 , где , где 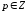 . .Задача 3. Используя тригонометрическую форму комплексного числа, произведите указанные действия: 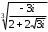 . .Решение:. Предположим, что 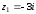 , а , а 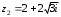 . Тогда: . Тогда:1) 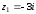 , где , где 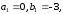 тогда тогда 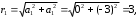 Находим значение главного аргумента 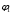 : :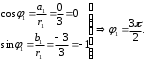 Представим 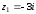 в тригонометрической форме, получим в тригонометрической форме, получим 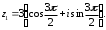 2) 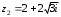 , где , где 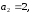 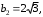 тогда тогда 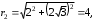 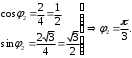 Представим 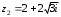 в тригонометрической форме, получим в тригонометрической форме, получим 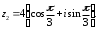 3) Найдем частное 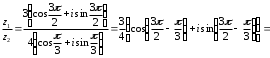 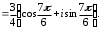 Далее, применяя формулу для извлечения корня степени 3, получим: 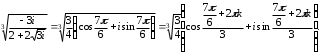 Так как корень степени 3, то в результате будет три значения искомого корня. Полагая k=0, 1, 2, получим: Если 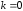 , то , то 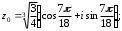 если 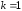 , то , то 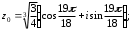 если 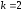 , то , то 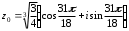 . .Ответ: 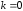 : : 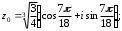 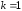 : : 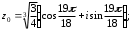 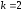 : : 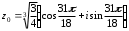 . .Статистические методы – мощный инструмент исследования во многих отраслях знаний. В географии, особенно в метеорологии и климатологии, статистика используется с начала регулярных метеорологических наблюдений [7]. Перепады температуры и атмосферного давления, распределение осадков, паводки рек, всё это и многое другое описывается математическим аппаратом теории экстремальных статистик. Одна из задач, которую решает данная теория, состоит в исследовании наблюдаемых максимальных и минимальных значений рассматриваемых величин. В данной работе предельные распределения описаны для независимых одинаково распределенных случайных величин. Таким образом, для применения предельных теорем необходимо, чтобы статистические данные удовлетворяли следующим условиям:независимость;одинаковое распределение;большой набор статистики. Применение теории экстремальных статистик непосредственно к исследованию максимальных и минимальных суточных значений температуры воздуха не является корректным, так как данные величины являются зависимыми. Поэтому для проведения анализа была взята величина скачка суточных максимальных температур воздуха в городе Курск за летний период с 1912 по 2017 год. Первым этапом исследования является проверка на независимость статистических данных с помощью линейного параметрического коэффициента парной корреляции, который вычисляется по следующей формуле 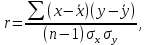 где 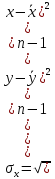 Коэффициент корреляции используется при наличии линейной связи между признаками. Если 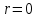 , то прямолинейная зависимость отсутствует. При , то прямолинейная зависимость отсутствует. При 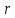 близком к близком к 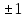 связь между признаками высокая, при связь между признаками высокая, при 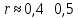 связь слабая, при связь слабая, при 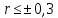 – весьма слабая [1]. – весьма слабая [1]. Для вычисления коэффициента корреляции в Excel был разработан макрос, с помощью которого посчитан коэффициент 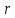 для каждого года с 1912 по 2017 год. Полученные результаты подтвердили факт, что связь между случайными величинами является слабой. для каждого года с 1912 по 2017 год. Полученные результаты подтвердили факт, что связь между случайными величинами является слабой. Следующим этапом исследования является подбор теоретической функции распределения к ряду наблюдений  С использованием непараметрического критерия Пирсона С использованием непараметрического критерия Пирсона 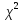 , статистика которого вычисляется по формуле , статистика которого вычисляется по формуле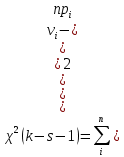 где k – общее количество интервалов, s – число параметров предполагаемого вероятностного закона исследуемых случайных величин, 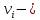 эмпирическая частота попадания вариант выборки в i-й промежуток [1], была проведена проверка гипотезы о нормальности распределения значений скачка максимальных суточных температур. Гипотеза о согласованности статистических данных с нормальным распределением с соответствующими параметрами, по критерию хи-квадрат подтвердилась. эмпирическая частота попадания вариант выборки в i-й промежуток [1], была проведена проверка гипотезы о нормальности распределения значений скачка максимальных суточных температур. Гипотеза о согласованности статистических данных с нормальным распределением с соответствующими параметрами, по критерию хи-квадрат подтвердилась. Для применения предельной теоремы выполнены все необходимые условия. Тогда согласно теории экстремальных статистик наибольшие годовые скачки максимальных суточных температур должны подчиняться двойному экспоненциальному закону распределения с центрирующей и нормирующей константами, вычисляемыми по следующим формулам 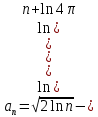 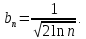 В связи с тем, что предельные теоремы справедливы в случае, когда 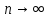 , а в нашем случае , а в нашем случае 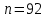 , то для , то для 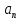 также необходимо учитывать бесконечно малую функцию также необходимо учитывать бесконечно малую функцию 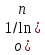 . Таким образом, . Таким образом, Оценка соответствия эмпирического распределения двойному экспоненциальному подтвердила, что во всех случаях отклонения фактических частот можно считать случайными и при уровне значимости 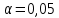 гипотеза о согласованности наибольших годовых скачков максимальных суточных температур с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 3.2.1. гипотеза о согласованности наибольших годовых скачков максимальных суточных температур с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 3.2.1.Рис.3.3.1. Гистограмма эмпирических частот. Таким образом, для моделирования независимых нормальных экстремальных климатических характеристик можно использовать двойное экспоненциальное распределение. Построение таких моделей важно не только для анализа природных явлений в настоящее время, но и для прогноза их развития в будущем. Тема изменения климатических условий стала очень популярной в последние десятилетия [7]. С развитием компьютерных технологий появились новые возможности обработки и анализа статистических данных, в том числе и в области метеорологии. Различные методы математической статистики позволяют не только вычислять разные климатические характеристики, но и моделировать метеорологические показатели [1]. Построение таких моделей важно не только для анализа природных явлений в настоящее время, но и для прогноза их развития в будущем. Цель данного исследования заключается в проведении анализа среднемесячных значений экстремальных суточных температур воздуха по городу Курск за март месяц с 1912 по 2017 года. Климатическая изменчивость среднемесячных значений максимальных и минимальных суточных температур воздуха за март месяц в городе Курск показана на Рис. 3.3.1. Рис.3.2.1 Климатическая изменчивость среднемесячных значений экстремальных суточных температур марта месяца в городе Курск 1912 – 2017г. Наблюдаемые и расчётные оценки параметров метеорологических процессов являются случайными величинами. Их вероятностное поведение описывается с помощью функции распределения, подбор которой осуществляется с учетом моментных характеристик. Наиболее значимыми среди них являются среднее значение, среднеквадратическое отклонение, асимметрия и эксцесс. Распределения метеорологических элементов, не имеющих легко достижимых физических пределов и асимметрия которых не очень велика (температура воздуха и почвы, атмосферное давление и т.п.) в большинстве случаев описываются нормальной функцией распределения [3]. Для исследования период наблюдений был разбит на два промежутка 1912-1971г. и 1972-2017г. С использованием непараметрического критерия Пирсона 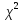 , была проведена проверка гипотезы о нормальности распределения среднемесячных значений экстремальных суточных температур марта месяца в городе Курск. , была проведена проверка гипотезы о нормальности распределения среднемесячных значений экстремальных суточных температур марта месяца в городе Курск.Гипотеза о согласованности статистических данных с нормальным распределением с параметрами, приведенными в таблице 1, по критерию хи-квадрат подтвердилась для обоих периодов. Далее была выполнена проверка на однородность анализируемых выборок. Гипотеза о равенстве дисперсий проверялась по F-критерию, статистика которого вычисляется по формуле: 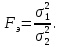 F-распределение определяется двумя параметрами: числом степеней свободы, зависящих от объемов выборок, 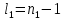 и и 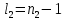 . В нашем случае . В нашем случае 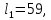 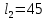 , критическое значение при уровне значимости , критическое значение при уровне значимости 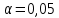 находим по таблице: находим по таблице: 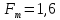 [1]. [1]. Если 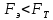 ,то различия между выборками не достоверны и гипотеза о равенстве принимается. В противном случае (если ,то различия между выборками не достоверны и гипотеза о равенстве принимается. В противном случае (если 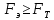 ) - гипотеза о равенстве дисперсий отвергается. ) - гипотеза о равенстве дисперсий отвергается.С помощью данного критерия было установлено, что разница между значениями дисперсий анализируемых периодов статистически незначима и для минимальных и для максимальных температур. Для определения однородности по средним значениям двух выборок использовался критерий Стьюдента (t-критерий), статистика которого вычисляется по формуле 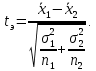 Параметры данного распределения - число степеней свободы 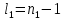 и и 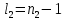 . При уровне значимости . При уровне значимости 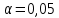 по таблице значений t-критерия критическая точка по таблице значений t-критерия критическая точка 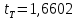 [1]. [1].Если 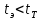 , то различия между выборками не достоверны и гипотеза о равенстве средних принимается. В противном случае (если , то различия между выборками не достоверны и гипотеза о равенстве средних принимается. В противном случае (если 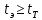 ) - гипотеза о равенстве средних отвергается. ) - гипотеза о равенстве средних отвергается.Результаты, полученные с использование данного критерия, подтверждают, что разница между средними значениями за оба периода является значительной и для минимальных и для максимальных температур. Таким образом, проведенный анализ эмпирических оценок параметров распределения выявил статистическую неоднородность среднемесячных значений экстремальных суточных температур за март месяц в городе Курск по указанным периодам, основанную на смещении средних значений величин в положительном направлении. Геометрические иллюстрации кривых плотностей, построенных по параметрам, приведенным в таблице 1, представлены на Рис.3.3.2 и Рис.3.3.3. Аналогичное исследование проводилось для среднемесячных значений среднесуточных температур [4]. Следует отметить, что во всех случаях кривые, построенные по наблюдениям за последний период, сместились вправо примерно на одну и ту же величину, а именно 2,4 C. Таким образом, ещё раз подтверждается факт, что в городе Курск имеется устойчивая тенденция к потеплению климата [4]. Тема изменения климатических условий стала очень популярной в последние десятилетия. С развитием компьютерных технологий появились новые возможности обработки и анализа статистических данных, в том числе и в области метеорологии. Различные методы математической статистики позволяют не только вычислять разные метеорологические характеристики, но и моделировать их изменения. Большинство методов статистического анализа оперируют с усредненными значениями выборки. Более того, в некоторых случаях крайние члены вариационного ряда вообще исключаются из рассмотрения или их влияние максимально нивелируется. Применение таких методов не позволяет проводить исследования закономерностей возникновения экстремальных метеорологических проявлений. В связи с этим целью настоящей статьи является разработка методики статистического анализа данных метеонаблюдений, позволяющей прогнозировать частоту появления экстремальных значений. Максимальные величины перепадов температуры и атмосферного давления, уровня осадков, паводков рек и других метеорологических показателей представляют особый интерес в различных сферах деятельности. Вероятности появления наибольших и наименьших значений в произвольной выборке описываются математическим аппаратом теории экстремальных статистик. Основные результаты теории экстремальных значений сформулированы для классической модели (схемы максимума независимых одинаково распределенных случайных величин при линейной нормировке) [Галамбош 1984]. Однако обобщения данной теории на неклассические случаи расширяют спектр ее приложений [Галамбош 1994, Лебедев 2005]. В проведенном исследовании в качестве статистических данных были взяты выборки, составленные из величин перепадов наибольших суточных температур воздуха в городе Курске в летние периоды за 102 года (с 1912 года), то есть 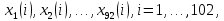 (1) (1)где 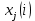 – разница между наибольшими суточными температурами воздуха j-го и (j-1)-го дня в i – й год (года занумерованы последовательно с 1912 года). – разница между наибольшими суточными температурами воздуха j-го и (j-1)-го дня в i – й год (года занумерованы последовательно с 1912 года). Наблюдаемые и расчётные оценки параметров метеорологических процессов являются случайными величинами. Их вероятностное поведение описывается с помощью функции распределения. Распределения метеорологических элементов, не имеющих легко достижимых физических пределов и асимметрия которых не очень велика (температура воздуха и почвы, атмосферное давление и т.п.) в большинстве случаев описываются нормальной функцией распределения [Исаев 1988]. Гипотеза о согласованности выше указанных статистических данных с нормальным распределением по критерию хи-квадрат подтвердилась. Далее с помощью линейного параметрического коэффициента парной корреляции было установлено, что взаимосвязь между элементами этих выборок является очень слабой и позволяет считать значения выборок независимыми. Таким образом, выборки (1) можно считать реализациями 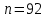 независимых, одинаково распределенных гауссовских случайных величин независимых, одинаково распределенных гауссовских случайных величин 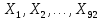 . .Далее была построена выборка из максимумов значений центрированных и нормированных последовательностей (1): 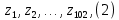 где 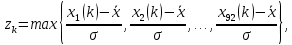 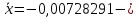 математическое ожидание, математическое ожидание, 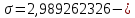 среднее квадратическое отклонение (вычислены по объединенной выборке). При этом максимумы последовательностей (1) (максимумы скачков наибольших суточных температур за летний сезон) среднее квадратическое отклонение (вычислены по объединенной выборке). При этом максимумы последовательностей (1) (максимумы скачков наибольших суточных температур за летний сезон)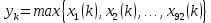 связаны с 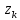 равенством: равенством: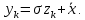 Таким образом, выборочные значения (2) представляют статистические данные для исследования и моделирования поведения случайной величины 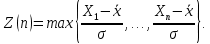 При этом 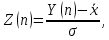 где 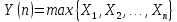 , ,следовательно, имеется равносильность событий 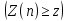 и и 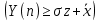 , то есть , то есть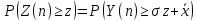 . .Статистическая согласованность выборки (1) с нормальным распределением позволяет для центрированных и нормированных максимумов перепадов температур (2), использовать предельное двойное экспоненциальное распределение: 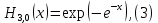 с центрирующей и нормирующей константами, вычисляемыми по следующим формулам 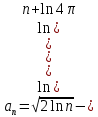 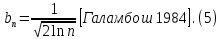 В связи с тем, что предельные теоремы справедливы при условии, что 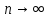 , то точность построенной модели во многом зависит от объема выборок, из которых берутся максимумы. Поскольку в нашем случае , то точность построенной модели во многом зависит от объема выборок, из которых берутся максимумы. Поскольку в нашем случае 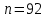 (объемы выборок, из которых выбирались максимумы), то для последовательности (объемы выборок, из которых выбирались максимумы), то для последовательности 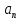 также необходимо учитывать возможность поправки порядка бесконечно малой функции также необходимо учитывать возможность поправки порядка бесконечно малой функции 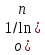 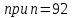 . .Таким образом, по формулам (4), (5) с учетом поправки вычислили значения центрирующей и нормирующей констант: 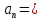 2,114405; 2,114405; 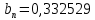 . .Оценка соответствия эмпирического распределения двойному экспоненциальному показала, что во всех случаях отклонения фактических частот можно считать случайными, и при уровне значимости 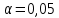 гипотеза о согласованности выборочных данных (2) с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 1. гипотеза о согласованности выборочных данных (2) с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 1. Таким образом, для моделирования поведения максимальных скачков наибольших суточных температур целесообразно использовать двойное экспоненциальное распределение. Построение моделей на его основе позволяет анализировать данные метеонаблюдений с точки зрения поведения наибольших суточных колебаний. Значения наблюдаемых и теоретических частот, вычисленных с помощью двойного экспоненциального распределения приведены в таблице 1. В таблице 2 представлены вероятности и соответствующие им относительные частоты событий 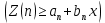 , состоящие в превышении максимом указанных значений. По результатам, представленным в этой таблице, наибольшая разница между относительной частотой и вероятностью указанных событий составляет 0,02. , состоящие в превышении максимом указанных значений. По результатам, представленным в этой таблице, наибольшая разница между относительной частотой и вероятностью указанных событий составляет 0,02. Используя теоретическое распределение (3) величины 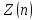 , можно сделать прогноз, что приблизительно в 95% летних сезонов значения максимальных скачков наибольших суточных температур воздуха будут менее 8,69 градусов. За рассмотренный период в 102 года скачок, превышающий это значение, наблюдался 3 раза, что составляет 3% от периода наблюдения . , можно сделать прогноз, что приблизительно в 95% летних сезонов значения максимальных скачков наибольших суточных температур воздуха будут менее 8,69 градусов. За рассмотренный период в 102 года скачок, превышающий это значение, наблюдался 3 раза, что составляет 3% от периода наблюдения .Таким образом, сравнительный анализ полученных теоретических и наблюдаемых частот событий, характеризующих поведение максимальных скачков наибольших суточных температур воздуха в летний сезон в городе Курске за столетний период наглядно иллюстрирует точность построенной модели и подтверждает возможность прогнозирования метеорологических показателей не только в области их усредненных значений, но и в области их экстремумов. Заключение В ходе выполнения курсовой работы, были решены следующие задачи: 1) Изложен основной материал по теме «комплексные числа» для классов с углубленным изучением математики. 2) Представлены решения задач с комплексными числами в алгебраической форме, отработаны основные операции сложения, вычитания, умножения, деления, операции сопряжения для комплексных чисел в алгебраической форме, степень мнимой единицы, модуль комплексного числа. 3) Разобраны задания связанные с геометрической интерпретацией комплексных чисел на координатной плоскости. 4) Рассмотрен и продемонстрирован алгоритм представления комплексных чисел в тригонометрической форме, а также вычисление комплексного числа в степени и извлечение корня. Материал, изложенный в данной курсовой работе, может быть использован при изучении курса алгебры в классах с углубленным изучением математики или на элективных курсах в школе. Список используемой литературыАбрамов А.М., Виленкин Н.Я., Дорофеев Г.В., Егоров А.А., Земляков А.Н., Моркович А.Г. Избранные вопросы математики. 10 класс. Факультативный курс. – М.: Просвещение, 1980. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений/ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 7-е изд. – М.: Просвещение, 2000. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.Ш. Алгебра и начала анализа. Пробный учебник 9-10 классов средней школы. – М.: Просвещение, 1975. Андронов И.К. Математика действительных и комплексных чисел. – М.: Просвещение, 1975. Беляева Э.С., Потапов А.С. Уравнения и неравенства первой степени с параметром и к ним сводимые. Учебное пособие. – Воронеж: ВГПУ, 2001. Болтянский В.Г., Сидоров Ю.В., Шабунин М.И. Лекции и задачи по элементарной математике. - М.: Наука, 1971. Вавилов В.В, Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачник по математике. Алгебра. Справочное пособие. – М.: Наука, 1987. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся школ и классов с углубленным изучением математики.– 6-е изд. – М.: Просвещение, 1998. Галицкий М.А., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1989. Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. – Воронеж: ВГПУ, 2004. Дадаян А.А., Новик И.А. Алгебра и начала анализа. – М.: Просвещение, 1987. Звавич Л.И. и др. Алгебра и начала анализа. Решение задач письменного экзамена. / Л.И. Звавич, Л.Я. Шляпочник, И.И. Кулагина. – М.: Дрофа, 2000. Карп А.П. Сборник задач по алгебре и началам анализа. Учебное пособие для учащихся школ и классов с углубленным изучением математики.– М.: Просвещение, 1995. Окунев Л.Я. Высшая алгебра. – М.: Просвещение, 1966. Петраков И.С. Математические кружки в 8 – 10 классах. – М.: Просвещение, 1988. Фадеев Д.К., Никулин М.С., Соколовский И.Ф. Элементы высшей математики для школьников. – М.: Наука, Главная редакция физико-математической литературы, 1987. Цыпкин А.Г., Пинский А.И. Справочник по методам решения задач по математике для средней школы. – М.: Наука, 1989. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: учебное пособие для 10 классов средней школы. – М.: Просвещение, 1989. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Арифметика и алгебра. – М.: Физматлит, Лаборатория Базовых Знаний, 2001. Энциклопедический словарь юного математика. (Составитель Савин А.П.). – М.: Педагогика, 1989. Яглом И.М. Комплексные числа и их приложения в геометрии. Изд. 2-е, стереотипное. – М.: Едиториал УРСС, 2004. |
