Практическое руководство-ФинМат. Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
Тема 11. Конверсия и замена рентНа практике часто сталкиваются со случаями, когда на этапе разработки условий контракта или в ходе его выполнения необходимо изменить условия выплаты ренты. Простейшими случаями конверсии являются: замена ренты разовым платежом (выкуп ренты); или наоборот: замена разового платежа рентой (рассрочка платежей). К более сложному случаю относится объединение нескольких рент в одну – консолидация рент. Цель проведения занятия – научиться рассчитывать характеристики заменяющих рент, используя формулы финансовых вычислений. Основные формулы Выкуп ренты. Этот вид конверсии сводится к замене ренты единовременным платежом, поэтому для вычисления размера разового платежа выбирается формула для нахождения приведенной стоимости аннуитета постнумерандо или пренумерандо: Рассрочка платежей. Рассрочка платежей – обратная задача к задаче выкупа ренты. Обязательство по уплате некоторой суммы заменяется равными платежами в рассрочку. Для решения задачи приравнивают современную стоимость ренты, с помощью которой проводится рассрочка, к сумме долга. Задача может заключаться в определении параметров этой ренты - члена ренты или ее срока, при условии, что остальные параметры заданы. Подобные задачи рассматриваются в лабораторной работе № 12. Объединение (консолидация) рент. Объединение рент заключается в замене нескольких рент с заданными параметрами новой рентой, параметры которой необходимо определить. В этом случае из принципа финансовой эквивалентности следует равенство современных стоимостей заменяющих и заменяемых (консолидированных) рент, что соответствует равенству: где PV- современная стоимость заменяющей ренты; PVi– современная стоимость i-той заменяемой ренты. Замена немедленной ренты на отсроченную. Пусть имеется немедленная рента с параметрами A, n, r. Необходимо отсрочить выплаты на t лет. В этом случае из принципа финансовой эквивалентности равенство приведенных стоимостей запишется следующим образом: где PV1- современная стоимость немедленной ренты; PV2 – современная стоимость отложенной ренты. Пусть срок отложенной ренты не изменяется, тогда неизвестный платеж отложенной ренты находится из уравнения: Где А1 - платеж исходной ренты А 2 – неизвестный платеж отложенной ренты t – время отложения ренты Пусть платеж отсроченной ренты не изменяется, тогда новый срок отложенной ренты находится из уравнения: где n2 – неизвестный срок отложенной ренты n1 – срок исходной ренты t – время отложения ренты в общем случае, когда Типовые задачи с решениями Задача 1. Пусть немедленная рента постнумерандо с условиями А=2 млн. руб. и сроком 8 лет откладывается на 2 года без изменения срока ренты. Сложная процентная ставка составляет 20% годовых. Необходимо найти платеж отложенной ренты. Решение По формуле (11.4) при А1 =2; t=2; r=0,2 А 2=2∙(1+0,2)2 А 2 =2,88 Отказ от немедленной выплаты ренты приводит к увеличению платежа до 2,88 млн.руб. Задача 2. Рента с ежегодными платежами в 2 млн. руб. и сроком 5 лет откладывается на три года без изменения сумм выплат. Найти новый срок ренты при условии, что на поступающие платежи ежегодно начисляются сложные проценты по ставке 8% годовых. Решение В соответствии с (11.5) при n1 =5; t=3; r=0,08; A=2 Отказ от немедленной выплаты ренты увеличивает ее срок до 6,689 года, т.е. на 1,689 года. Пусть продолжительность новой ренты в целых годах равна 6. тогда приведенная стоимость новой ренты составит Современная стоимость исходной ренты составит Разность в сумме 0,6458 млн. руб. необходимо уплатить в начале действия контракта. Задача 3. Пусть немедленная рента постнумерандо с условиями А=2 млн. руб. и сроком 8 лет откладывается на 2 года с изменением срока ренты до 11 лет. Сложная процентная ставка составляет 20% годовых. Необходимо найти платеж отложенной ренты. Решение По формуле (11.6) при А1 =2; t=2; r=0,2; n1=8; n2=11 Платеж отложенной ренты равен 2,5539 млн.руб. Задача 4. Банк предлагает ренту постнумерандо на 15 лет с полугодовой выплатой 100 тыс. руб. Годовая процентная ставка в течение всего периода остается постоянной, сложные проценты начисляются по полугодиям. По какой цене можно приобрести эту ренту, если выплаты будут осуществляться 1) через 3 года; 2) немедленно, а сложная процентная ставка равна 4% годовых? Решение. 1) используем формулу (11.3), считая полугодие базовым периодом, при t=6 PV=100FM2(2%,6)FM4(2%,30)=1000,88822,3965=1988,809 Ренту можно приобрести за 1 988 809 руб. 2) используем формулу (11.3), считая полугодие базовым периодом при t=0 PV=100FM4(2%, 30)=10022,3965=2239,65 Ренту можно приобрести за 2239650 руб. Задача 5. Три ренты постнумерандо - немедленные, годовые, заменяются одной отложенной на три года рентой постнумерандо. Согласно договоренности заменяющая рента имеет срок 10 лет, включая отсрочку. Характеристики заменяемых рент: А1 =100; А2 =120; А3 =300 (тыс. руб.); n1=6; n2=11; n1=8 лет. Необходимо:
Решение Данные для определения приведенных стоимостей заменяемых рент занесем в таблицу:
Платеж заменяющей ренты равен 960 189 руб. Если бы заменяющая рента была бы немедленной, ее платеж находим из уравнения:
PV=2002,946∙(1+0,2)3 =3461,091 Неизвестный срок ренты находим из формулы (10.4) (Занятие № 10): 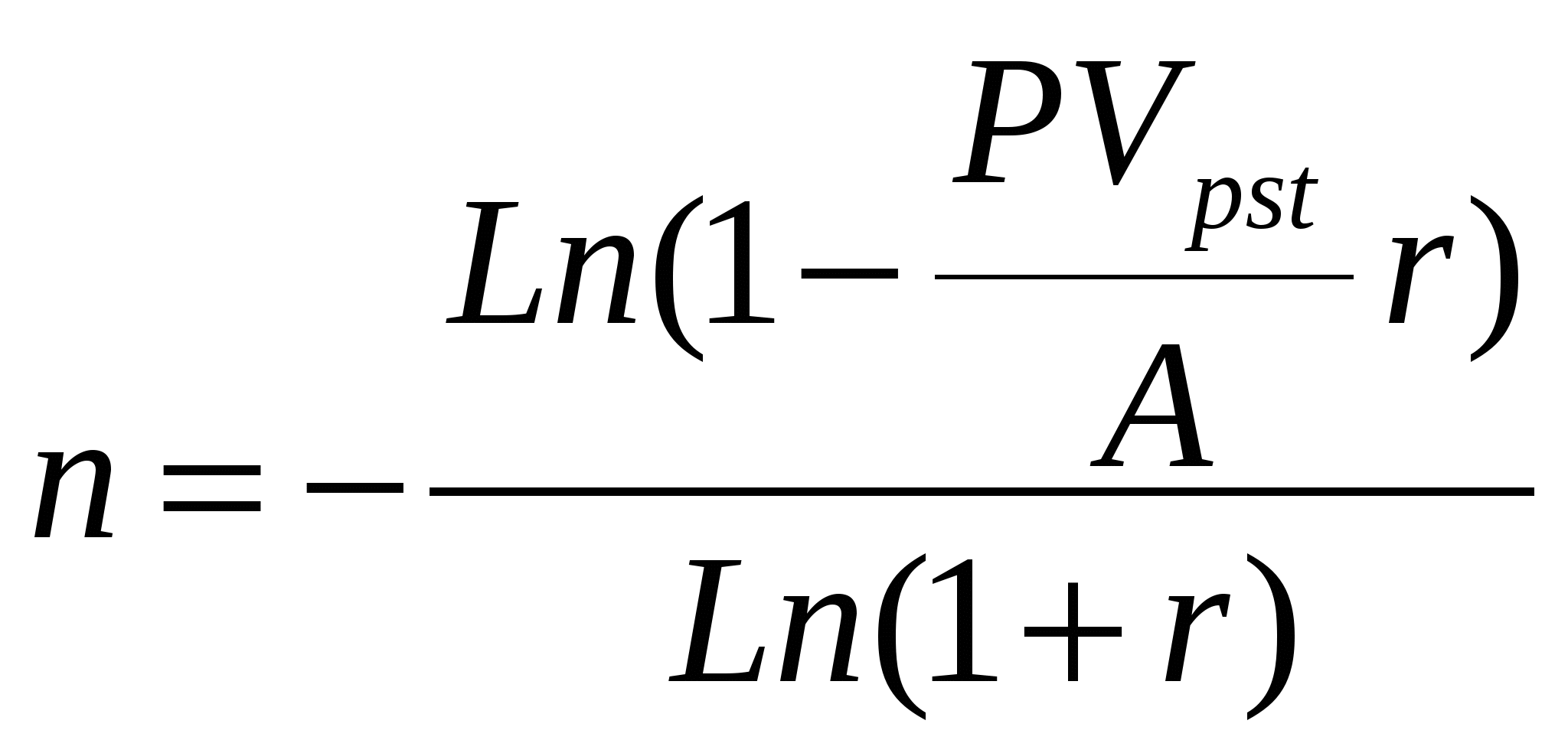 при А=1500; r=20%; PV=3461,091 при А=1500; r=20%; PV=3461,091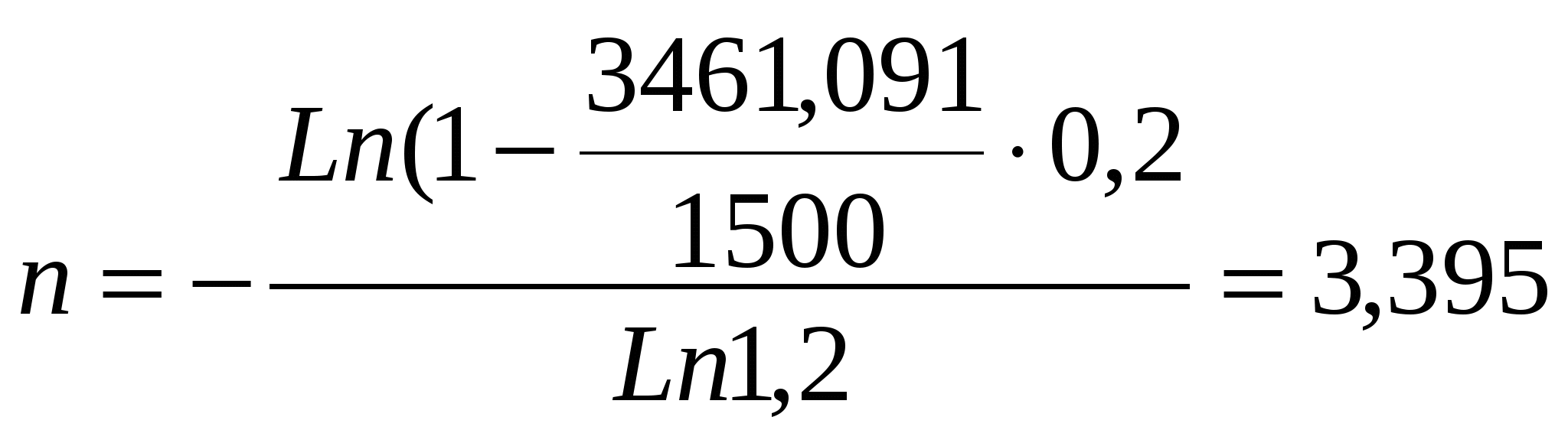 Установим срок заменяющей ренты 4 года. При этом приведенная стоимость ренты равна PV=1500∙FM4(20%,4)=1500∙2,5887=3883,05 Излишек в сумме 3883,05-3461,091=421,959 компенсируем в начале финансовой операции. Задачи для самостоятельной подготовки Задача 1. Найти годовую ренту - сумму сроком в 10 лет для двух годовых рент: одна продолжается 5 лет с годовым платежом 1 млн. руб., другая - продолжительностью 8 лет и годовым платежом 0,8 млн. руб. Годовая ставка сложных процентов равна 8%. Задача 2. Необходимо выкупить полугодовую ренту с платежами в 50 тыс. руб., срок ренты – 10 лет; сложные проценты по ставке 10% начисляются по полугодиям. Задача 3. Годовая рента постнумерандо с платежами А=200 тыс. руб. и сроком 8 лет откладывается на 2 года без изменения срока самой ренты. Процентная ставка для пролонгирования равна 10% годовых. Определить размер платежа отложенной ренты. Как изменится ответ, если платежи в отложенной ренте будут производиться в начале года? Задача 4. Рента постнумерандо с платежами А=500 тыс. руб. и сроком 10 лет откладывается на 3 года без изменения сумм выплат. Определить срок отложенной ренты при ставке пролонгирования 12% годовых. Задача 5. Три ренты пренумерандо - немедленные, годовые, заменяются одной отложенной на два года рентой постнумерандо. Согласно договоренности заменяющая рента имеет срок 6 лет, включая отсрочку. Характеристики заменяемых рент: А1 =200; А2 =120; А3 =100 (тыс. руб.); n1=6; n2=11; n1=8 лет. Необходимо:
Задача 6. Индивидуальный предприниматель погашает кредит равными ежемесячными платежами в 100 тыс. руб. в течение 3 лет. Банк согласился уменьшить платежи до 80 тыс. руб. Насколько увеличится срок погашения кредита, если банк использует сложную ставку 12% годовых с ежемесячным начислением процентов? Контрольные вопросы
|
