Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 21 из 26

14 ДІЛЕННЯ БІНАРНИХ ЧИСЕЛ

14.1 Методи ділення бінарних чисел

Найбільше поширення одержали наступні методи виконання операції ділення чисел:

1. На кожному кроці з діленого віднімається дільник (починаючи зі старших розрядів) стільки разів, скільки це можливо до одержання залишку менше дільника. У частці записується цифра, рівна числу цілих частин дільника N. L  залишок. A: B= NB+L

2. Інший метод ділення полягає в множенні діленого на обернену величину З=А:В=АВ^-1=А1/В.

Тут виникає проблема знаходження обернених величин шляхом розкладання в біноминальний ряд Ньютона, використовуючи модель розкладання бінома ступеня m: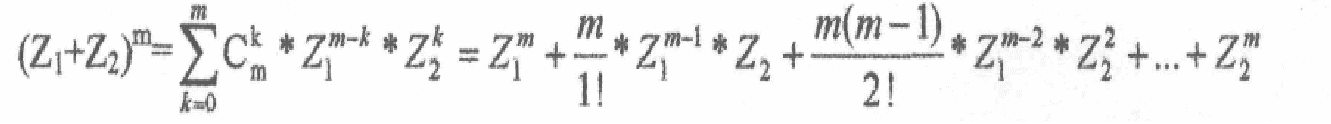

де C^k_mбіномінальні коефіцієнти число різних сполучень із m різних змінних по k у кожному сполученні: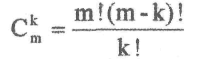



3. У третьому методі використовують наближені формули знаходження частки, які зводять операцію розподілу до операції додавання, вирахування, множення.

Перший розглянутий метод відносять до “шкільних” алгоритмів ділення з відновленням залишку. Розглянемо приклад розподілу в бінарній арифметиці.

П
Ділене _1100100| 1010Дільник

1010 1010

_00101 Перший залишок (позитивний)

1010

^_1011 Другий залишок (негативний)

+1010 Відновлення залишку

_ 01010

1010

0000

риклад: А_м=00/1100100. (100₍₁₀₎); В_м=00/1010. (10₍₁₀₎). Рішення наведене нижче (використано правила бінарного віднімання).





14.1.1 Алгоритм ділення з відновленням залишку

Формально алгоритм описується в такий спосіб. Нехай А  ділене, В  дільник, С  частка: A=0,α₁α_2...α_n; B=0,b₁b₂...b_m, C=0,c₁c₂...c_r.

На кожному кроці визначається залишок А_i=A_i-1B2^-i, проводиться аналіз: якщо залишок А_i>0, то в старший розряд частки записується C_i=l, робиться лівий зсув і перехід до визначення наступного залишку. Якщо A_i<0, то С_i=0 і відновлюється залишок A_i=A_i-1+B2^-i, а на наступному кроці після зсуву визначається новий залишок і т.д.

Даний алгоритм ділення з відновленням залишку реалізується на двійкових суматорах оберненого (ДСОК) або доповняльного (ДСДК) кодів. Структурна схема наведена на рис. 14.1.

Частковий залишок (частка) виходить в результаті послідовного виконання операції віднімання (із заміною віднімання на додавання в доповняльному коді), тому частіше застосовується суматор ДСДК для алгебраїчного додавання.









Регістр діленого

Пристрій керування

Аналізатор

знака

Регістр залишка

Регістр

дільника




СУМАТОР


Рисунок 14.1  Структурна схема ЦА операції ділення