Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 19 из 26

12 МНОЖЕННЯ ЧИСЕЛ НА ДСДК

З одного боку, якщо числа зберігаються в ЦА в доповняльних кодах, то і операцію множення зручно робити на ДСДК. З іншого боку, при множенні на ДСДК виникають проблеми, усунути які можна з огляду на певні правила.

12.1 Множення чисел на ДСДК при позитивному множнику

При позитивному множнику для ДСДК діє наступне правило.

Правило. Добуток доповняльних кодів співмножників дорівнює допо-вняльному коду результату тільки при позитивному множнику В>0.

Дійсно: нехай А  будь-яке число, тоді А = А_доп і якщо В>0, тоді маємо:

_{АВ=Адоп0,b1b2...bnАдопb12-1+Адопb22-2+...+Адопbn2-n.}

На основі раніше розглянутої теореми про додавання доповняльних кодів, робимо висновок, що результат множення представлений у доповняльному модифікованому коді.

Можна сформулювати алгоритм множення чисел на ДСДК.

Якщо множник більше "0", то множення на суматорі доповняльного модифікованого коду полягає в наступному. Аналізується розряд множника, починаючи з молодшого. При в_і= 1, до вмісту суматора додається множене. При в_і = 0, до вмісту суматора нічого не додається. Після кожного аналізу і додавання виробляється модифіковане зсув суматора і множника вправо на один розряд.

Приклад. Помножити числа А=0\10101 (21), В=0\10011 (+19).

Метод 2. ДСДК. Запишемо числа А^м_доп =11\01011; В^м_доп=00\10011. Суматор має 7 розрядів, РгВ 5 розрядів. Рішення наведено в таблиці 12.1.

Результат отриманий у доповняльному коді зі знаком мінус (11). Після перетворення його в прямий код(C_пр=11/0110001111) знак збері-гається Для зменшення апаратних засобів, результат зберігається в суматорі і РгВ (при зсувах молодші розряди суматора надходять у старші розряди РгВ).
Таблиця 12.1  Множення чисел на ДСДК (метод 2, В >0)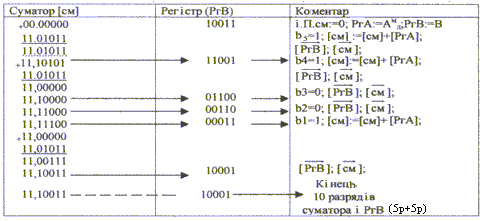

12.2 Множення чисел на ДСДК при негативному множнику

Другий випадок, коли А  будь-яке число, а множник В<0., де означає +1

На основі |А|+[А_доп] = q, де |A|  абсолютне значення числа А. Доповняльний код є математичним доповненням до числа основи системи числення 1. Тому (для двійкового коду) можна записати, що –В=В_м = В_доп2 (тому що – (В+[В_доп])= 2). Тоді, АВ=А (В_доп2).

Отже, добуток чисел . (З урахуванням того, що число В негативне і значущі цифри його доповняльного коду мають значення |[В_доп]|=1|В|).

Таким чином, при негативному множнику добуток доповняльних кодів операндів не дорівнює доповняльному коду результату. Якщо (А) замінити на , то можна ввести правило.

Таблиця 12.2  Множення чисел на ДСДК при В<0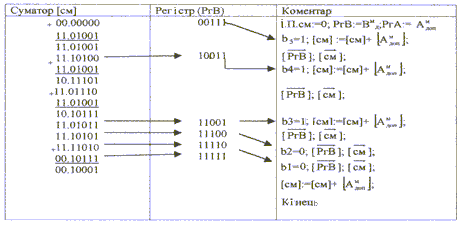



ПРАВИЛО. Якщо множник негативний, то добуток чисел на суматорі доповняльного коду дорівнює додатку виправлення +1 до добутку доповняльних кодів співмножників. При цьому, виправлення  це повністю інвертоване , включаючи і знак з додаванням 1 до молодшого розряду.

Приклад. Помножити числа А=10111 (23) і В=11001 (25) на ДСДК (метод 2).

Підготовчі роботи. Запишемо: А^м_доп =11\01001; В^м_доп =11\00111; (А)==00\10111.

Рішення наведено в таблиці 12.2. С = 00\1000111111 (+575).

Перевірка: (23)(25)=+575

Таким чином, при множенні чисел на ДСДК одержуємо одночасно знакову і цифрову частини добутку С=АВ.