Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 20 из 26

13 МНОЖЕННЯ ЧИСЕЛ НА ДСОК

13.1 Множення чисел на ДСОК при позитивному множнику

За аналогією із ДСДК, при множенні операндів заданих у оберненому модифікованому коді, розглянемо два випадки: В>0 і В<0.
Випадок В0. Добуток обернених кодів співмножників дорівнює оберненому коду результату тільки у випадку позитивного множника.

Доказ. Нехай множене А=А_об., а множник В>0. Тоді: АВ=А_об0,b₁b₂...b_n = А_обb₁2^-1+А_обb₂2^-2+...+А_обb_n2^-n. У правій частині виходить обернений код результату тому що В=В_об. Це означає, що множник В позитивний.
Алгоритм. Множення на ДСОК (при В>0) виконується в наступній послідовност (наведена в таблиці 13.2):

- у суматор записуються 11.111...1 (машинний нуль оберненого коду);

- у регістр В записується множник у прямому коді. Ведеться аналіз розрядів РгВ (починаючи з молодшого), і якщо там "1", то до вмісту суматора додається обернений код множеного. Якщо там 0, то до суматора нічого не додається;

- після циклу додавання і аналізу, виробляється зсув вправо вмісту суматора і РгВ на один розряд (можна з переносом молодших розрядів суматора в старші розряди РгВ);

- якщо знак результату негативний, то він у оберненому коді і необхідне перетворення в прямий код;

-після перетворення в прямий код, перевіряємо нормалізацію результату.
Приклад. Помножити на ДСОК числа: А = 0/10011; В = 0/11001. Запишемо числа в машинному зображенні:

А^м_об=11/01100; В^м_об=00/11001.

Таблиця 13.1  Множення на ДСОК при позитивному множнику В0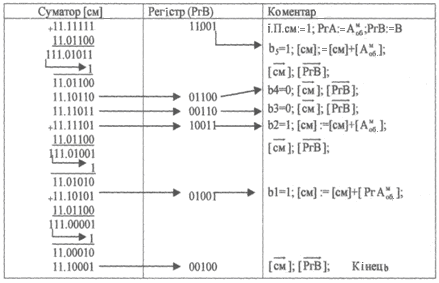



Відповідь С^м_об=11/1000100100; С_пр= 111011011.

13.2 Множення чисел на ДСОК при негативному множнику

Випадок В0. Якщо множник негативний, то добуток чисел на суматорі ДСОК є додатком виправленя А  і [A]_об2^-n до отриманого добутку обернених кодів співмножників.
Доказ. Нехай А=[A]_об і В<0, тоді ; відповідно до подання у ФРК, фіксовано перед старшим розрядом |B|+[B]_об=qq^-n=22^-n; звідси [В]_об=2+В2^-n; тож,+ 2^-n1, добуток дорівнює: АВ =A_об+[A]_об (2^-n)+; є два виправлення: перше [A]_об(2^-n) порівняне мале (тому часто ігнорується) і друге +.

Алгоритм. Множення на ДСОК (при В0) виконується в наступній послідовності (наведена в таблиці 13.2):

- у суматор записуються 11.111...1 (машинний нуль оберненого коду);

- у регістр В записується множник у оберненому коді (без знака);

- у суматор додається множене у оберненому коді А_об;

- ведеться аналіз розрядів РгВ (починаючи з молодшого), і якщо там «1» («0»), то до вмісту суматора додається (нічого не додається) обернений код множеного;

- після циклу додавання і аналізу робиться зсув вправо вмісту суматора і РгВ на один розряд (можна з переносом молодших розрядів суматора в старші розряди РгВ);

- після аналізу і зсуву старшого розряду множника до результату додають виправлення []  інверсію А_об, включаючи і знак;

- якщо знак результату негативний, то він у оберненому коді і необхідне перетворення у прямий код;

- після перетворення в прямий код, необхідно перевірити нормалізацію результату.

Приклад. Метод 2, множення чисел на ДСОК. А=0/110101; В=0/101000; АВ=+2120. Рішення: Запишемо машинне зображення чисел.

А^м_об = 11/001010; В^м_об = 11/010111; = 00/110101.

Послідовність виконання операції множення наведена в таблиці 13.2.

З урахуванням розрядів РгВ будемо мати 100\100001000111. Переповнення «1» із знакового розряду Sg₁ додається до молодшого розряду числа. Тоді, одержимо відповідь: С_пр=00\100001001000=2120₍₁₀₎.
Існує ряд методів множення заснованих на роздільному під-сумковуванні груп часткових доданків з наступним об’єднанням сум з урахуванням переносів. Роздільна обробка проміжних сум і переносів вимагає так званого "дерева суматорів" (використано в IBM-360).

Таблиця 13.2  Множення на ДСОК при негативному множнику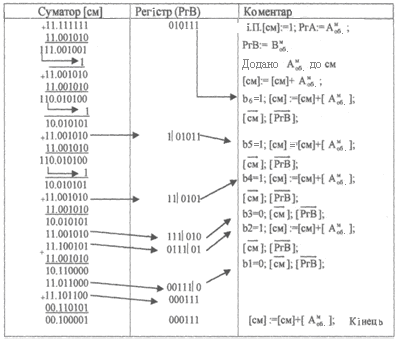



Існують також прискорені методи множення, засновані на використанні матриць проміжних результатів. Розглянемо схему множення:

A = a₅, a₄, а₃, а₂, a₁

*B = b₅, b₄, b₃, b₂, b₁

a₅b₁ а₄b₁ а₃b₁ а₂b₁ а₁b₁

+.........................................

а₅b₅ а₄b₅ а₃b₅ а₂b₅ а₁b₅

С₁₀ С₉.......................С₂ С₁

Цю схему можна представити також у вигляді матриці таблиці 13.3. Кожний елемент цієї матриці дорівнює "0" або "1".

Таблиця 13.3 Матричне множення чисел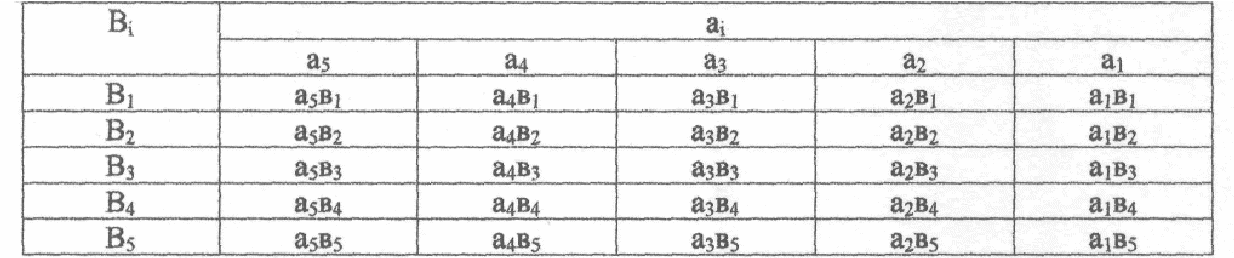



Добуток двох чисел можна одержати, якщо підсумувати елементи матриці в діагональному порядку. Cкладати доводиться тільки 0 або 1, тому операцію додавання можна виконувати за допомогою напівсуматорів і суматорів на один двійковий розряд.

Рисунок 13.1  Структурна схема пристрою множення для реалізації матричного алгоритму



Рисунок 13.2  Схема множного пристрою за алгоритмом Дадда

Найбільше поширення одержали алгоритми Дадда, Уоллеса (матричний) і алгоритм збереження переносів [1-21]. На рис. 13.1 представлена структурна схема матричного пристрою множення для реалізації матричного алгоритму.

Алгоритми відрізняються друг від друга групуванням часткових добут-ків, кількістю етапів перетворень. Для матричного алгоритму  чотири етапи перетворення, для алгоритму Дадда – три етапи. Однак, матричні методи множення, незважаючи на більший об’єм устаткування, дають великий виграш часу, а використання ВІС значно знижує обмеження на устаткування.

Розглянуті методи множення знайшли широке застосування в практиці бінарної арифметики.