Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 17 из 26

11 МНОЖЕННЯ ДВІЙКОВИХ ЧИСЕЛ

11.1 Методи множення бінарних чисел

Розглянемо основні способи виконання операції множення для різних систем. Найпоширенішим способом множення чисел є спосіб порозрядного множення множеного на множник, починаючи з молодшого розряду (1-й спосіб), починаючи зі старшого розряду (2-й спосіб). Розглянемо приклад: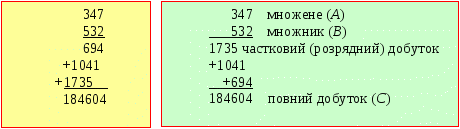



Аналіз способів множення чисел в десятковій системі показує, що операція множення складається з порозрядного множення множеного на множник з перенесенням переповнення в старший розряд, зрушення часткових добутків на один розряд вліво (вправо), підсумовування часткових добутків.

У двійковому численні це завдання значно спрощується, оскільки множити порозрядно немає необхідності. Насправді, якщо множити множене на "1", то це повторення множеного із зсувом на один розряд вправо (вліво), а на "0"  записуються одні нулі із зрушенням.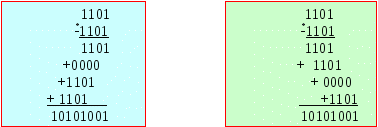



В обох випадках операція множення складається з ряду послідовних операцій зсуву і складання часткових добутків. Таким чином, операція множення зводиться до складання часткових добутків, які виходять з множеного або нулів, якщо в розряді множника «нуль», або множеного, якщо в розряді множника «одиниця» і відповідним або зсувом.

Окрім операції складання, при виконанні множення, з’являється операція зсуву чисел. При цьому, можливі два варіанти:

- зсувати множене відповідно до вказівок множника;

- зсувати суму часткових добутків.

Розглянемо основні методи виконання операції множення ЦА.

МЕТОД 1. Нехай А  множене > 0, В  множник > 0, а С  добуток.

Запишемо числа у ФФК: A=0,α₁α_2,...,α_n; B=0,b₁,b₂,...,b_n (А і В правильні дроби). В  множник і він визначає розрядність С (чим він більший, тим більша розрядність С). Тоді, B=b₁2^-1+b₂2^-2+...+b_n2^-n.

Звідси: C=AB = 0,α₁α_2... α_n(b₁2^-1+b₂2^-2+.. .+b_n2^-n)=

_{=(2-10,α1α2... αn)bl+(2-20,α1α2... αn)b2+...+(2-n0,α1α2... αn)bn.. (11.1)}

Множник 2^-n означає зсув на n розрядів вправо числа, що укладено в дужки, тобто зсуваэться вправо множене і множення на множник починається зі старших розрядів. Структурно це зображено на рис. 11.1.



Рисунок 11.1  Метод множення зі зрушенням вправо множеного

МЕТОД 2. Нехай A=0,α₁α_2... α_n  множене; B=0,b_lb₂...b_n множник. Перетворимо множник по методу Горнера:

<sub>B=(...((bn2-1+bn-1)2-1+bn-2)2-1+...+b2)2-1+b1)2-1.

Тоді,

C=AB=(...(bn0,α1α2...αn)2-1+bn-10,α1α2...αn)21+...+b10,α1α2...αn)2-1, (11.2)</sub>

За цією моделлю, множення починається з молодших розрядів і вправо зрушується. Структура наведена на рис. 11.2



Рисунок 11.2  Метод множення зі зрушенням вправо суми часткових добутків

МЕТОД 3. Нехай A=0,α₁α_2...α_n  множене; B=0,b_lb₂...b_n – множник. Використовуючи метод Горнера, запишемо множник:

<sub>B=2-n(b12n-1+b22n-2+...+bn-121+bn20). Тоді,C=AB=

=2-n(bn0,α1α2...αn+(210,α1α2...αn)bn-1+...+(2n-10,α1α2...αn)b1 (11.3)</sub>
Це означає: множення починається з молодших розрядів і множене зсувається вліво на один розряд у циклі. Структура представлена на рис.11.3.



Рисунок 11.3  Метод множення зі зрушенням вліво множеного на один розряд у циклі

МЕТОД 4. Нехай A=0,α₁α_2...α_n  множене; B=0,b_lb₂...b_n – множник. Запишемо В  множник по методу Горнера, як у попередньому методі. Тоді, C=AB=

=2^-n(...(2¹(b₁0,α₁α_2...α_n)+b₂0,α₁α_2...α_n)2¹+…

+b_n10,α₁α_2...α_n)2¹+ +b_n0,α₁α_2...α_n). (11.4)

За цією моделлю множення починається зі старшого розряду і в кожному циклі сума часткових добутків зрушується вліво. Схема такого множного пристрою наведена на рис.11.4.



Рисунок 11.4  Метод множення зі зрушенням вліво суми часткових добутків

Таким чином, для реалізації операції множення необхідно мати, як мінімум: суматор, регістри для зберігання множеного й множника, схему аналізу розрядів множника. Суматор і регістри повинні мати ланцюги зсуву вмісту в ту або іншу сторону відповідно до прийнятого методу множення.