Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 25 из 26

16.2 Характеристики бінарно (двійково)-десяткових кодів

Розглянемо основні характеристики і область застосування двійково-десяткових кодів (ДДК) систем числення, наведених у таблиці 16.1.

16.2.1 Код із природними вагами 8421

У цьому коді кожна десяткова цифра представлена у звичайній бінарній системі числення. Використовується код при перекладі чисел з десяткової системи у двійкову, індикації роботи регістрів, суматорів, лі-чильників і ін. пристроїв. В арифметичних операціях застосовується рід-ко через труднощі виділення переносів і одержання доповняльності до 9.

Приклад. Записати число 765 у ДДК 8421.

Рішення. Записується кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=0111.0110.0101

16.2.2 Код 8421+3 (код з надлишком 3)

У цьому коді до кожної десяткової цифри додається 3. Код не відповідає вимозі виваженості. Застосовують його найчастіше в десятковій арифметиці, тому що легко виділяється десятковий перенос.

Приклад. Записати число 765 у ДДК 8421+3.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів і надлишком +3: 765=1010.1001.1000

16.2.3 Код 2421

Код 2421 (аналогічний 4221) задовольняє всім п’яти вимогам. Однак, не має властивість адитивності, що утруднює виконання арифметичних операцій. Застосовувався в закордонній ЕОМ «МАРКО-3».

Приклад. Записати число 765 у ДДК 2421.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=1101.110.1011.

16.2.4 Код 7421

У цьому коді будь-яка цифра зображується не більш ніж із двома одиницями, що знижує споживання струму. Не відповідає вимозі доповняльності.

Приклад. Записати число 765 у ДДК 7421.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=1000.0110.0101.

16.2.5 Код 5211

Стверджується, що пристрої (лічильники, регістри і ін.) побудовані на основі цього коду, більш економічні за устаткуванням. Застосовувався в ЕЦОМ типу «ПРОМІНЬ».

Приклад. Записати число 765 у ДДК 5211.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=1100.1010.1000.

16.2.6 Код 5421

Цей код використається для прискорення виконання деяких арифметичних операцій. Наприклад, при множенні на цифри 2 і 5 переніс поширюється на один розряд вперед, а при множенні на 4 - на два розряди вперед. Це дозволяє організувати множення на ці цифри апаратними засобами зі схемною реалізацією.

Приклад. Записати число 765 у ДДК-5421.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=1010.1001.1000.

16.2.7 Код 8-4-21

У цьому коді число, що перевищує дев’ять, виходить за межі тетради, що прискорює формування переносу при виконанні операцій підсумовування.

Приклад. Записати число 765 у ДДК 8-4-21.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів і їхніх знаків: 765=1011.1010.1101.

16.2.8 Код 2 з 5 (7421mod2)

Цей код виходить із коду 7421 шляхом додавання праворуч п’ятого розряду, куди проставляється сума цифр основної тетради, узятої по mod 2, за винятком цифри 0. Цифра 0 має штучне зображення 11000.

Відмінність коду полягає в тому, що всі двійкові еквіваленти десяткових цифр мають дві одиниці. Такі коди називають рівноважними, їх використовують для виявлення асиметричних, одиночних помилок. Імовірність компенсованих (подвійних) помилок надзвичайно мала. Ще однією достойністю коду є рівномірне навантаження на джерело живлення (використано в ЕОМ ІВМ-7070).

Приклад. Записати число 765 у ДДК 2 з 5.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=10001.01100.01010.

16.2.9 Код 84-2-1

Код 84-2-1 добре формує переноси в старший розряд при порозрядному додаванні, тому що вже цифра 9 має у всіх розрядах одиниці  1111.

Приклад. Записати число 765 у ДДК 84-2-1.

Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів і їхніх знаків: 765=1001.1010.1011.

16.3 Виконання операції додавання в кодах ДДК

Правила операції додавання будемо розглядати тільки для конкретних кодів, тому що вони не можуть бути універсальними (тобто відповідати всім вимогам п. 16.1) через те, що кожний тип кодів має свою конкретну специфіку.

Нехай задані десяткові числа: А=а₁а₂…а_n, B=b₁b₂…b_n, і результат операції їх додавання C=c₀c₁…c_n, де а_і, b_і, с_і десяткові цифри, представлені бінарними кодами тетрад.

Операція додавання виконується порозрядно з урахуванням додавання до і-ого розряду переносу переповнення з попереднього молодшого розряду р_і+1 і відрахування переповнення р_іпри переносі його в старший р_і-1 розряд:

_{сі=аі+ві+рі+1(рі10).}

В окремому випадку, переносів переповнення може і не бути.

16.3.1 Операція додавання в ДДК 8421

При додаванні десяткових чисел у ДДК 8421 потетрадно, виконується бінарне, порозрядне додавання, при цьому можуть виникнути наступні випадки.

1. Коли с_і  10, тому переповнення немає і перенос у наступний розряд не виникає, тобто: с_і=а_і+в_і+р_і+1  10.

Приклад. +3 (0011)

+5 (0101)

+8 (1000).

2. Коли с_і  10. Тут виникає десятковий перенос і сума повинна бути дорівнює с_і=а_і+b_і+р_і+1(р_і10). Однак, якщо перенос виділився автоматично тобто с_і  16, то в наступний розряд йде перенос рівний 16, а не 10. Якщо ж перенос не виділився автоматично, тобто 10≤с_і≤15, то для с_і вийшла заборонена комбінація. В обох випадках до суми необхідно додавати корекцію 6 (0110), що автоматично усуває заборонені комбінації. При цьому, в і-ому розряді залишається необхідне значення двійкового коду десяткового числа, а в старший розряд переходить двійкова одиниця еквівалентна 10. Приклади.

16.3.2 Операція додавання в ДДК 8421+3

У цьому коді при двійковому додаванні також можуть бути два випадки.

1. Сума розряду с_і=а_і+b_і+р_і+110. Тому що цифри а_і і b_і вже мали надлишок три кожна, то сума буде мати надлишок шість. Тому, для одержання правильного результату, із суми необхідно відняти три, а три залишаться як надлишок +3. У машинних алгоритмах замість вирахування трьох до суми додають число 13 (1101), тому що 13=163, і тим самим блокують поширення переносу р_і=16, що рівноцінно вирахуванню 16.

Приклади.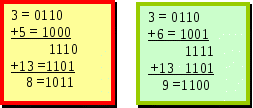

2. У цьому випадку сума розряду перебуває в межах 10≤с_і=а_і+b_і+р_і+1≤19, тому перенос формується автоматично. У наступний старший розряд переходить перенос р_і=16, тому, для відновлення надмірності коду, до отриманої суми необхідно додати три.

Цей код використовувався в деяких моделях машин ЄС при виконанні операції додавання.

П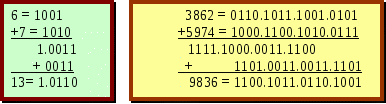
риклади.

16.3.3 Операція додавання в ДДК 2421

Таблиця кодування цього коду наче би ділиться на дві частини: від 0 до 4 йдуть нормальні двійкові числа, починаючи з 5, кожна тетрада містить надлишок 0110.

При додаванні можуть виникнути три випадки.

1. Якщо складають цифри, що, менше 5 і результат додавання теж менше 5, то корекції не потрібно, тому що він представлений у звичайній бінарній системі.

Якщо с_і=а_і+b_і+р_і+1≥5, то результат повинен бути збільшений на шість (0110).

Ознакою даної корекції є одержання заборонної комбінації при додаванні. Приклади.

3 = 0011

+4 = 0100

1 = 0001

1000

0110

8 = 1110

1 = 0001

+2 = 0010

3 = 0011

2. Якщо один з додатків більше 4 і результат перебуває в діапазоні 15а_і+b_і+р_і+1 ≥5, то корекція не потрібна, тому що в ньому є надлишок 6.

3. Якщо обидва з додатків більше 4 і 10≤а_і+b_і+р_і+115, то з результату треба відняти 6 (0110), якщо ж а_і+b_і+р_і+115, то корекція не потрібна. Звичайно, вирахування шістки міняють на додавання десяти (1010) з відкиданням виниклого переносу.

П
7279 = 1101.0010.1101.1111

+3658 = 0011.1100.1011.1110

1.0000.1111.1001.1101

+ 0000.0000.1010.0000

10937 =1.0000.1111.0011.1101
риклади.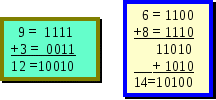