Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів

• Название: Щербаков а. Н., Проскурін м. П., Грушко с. С. Прикладна теорія цифрових автоматів
• Анкор: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Дата: 13.02.2018
• Размер: 2.54 Mb.
• Имя файла: Ukr1_PTTsA_kl_ch1_10-02-2010.doc
• Тип: Протокол; #15521
• страница: 26 из 26

17 АРИФМЕТИЧНІ ОПЕРАЦІЇ В СИСТЕМІ ЗАЛИШКОВИХ КЛАСІВ

Розглянемо основні правила виконання арифметичних операцій у системі залишкових класів (див. гл. 2). Нехай задано набор основ: р₁=3; р₂=5; р₃=7.

Тоді діапазон чисел, що можна представити буде дорівнювати Р=р₁р₂р₃=105. Числа будемо представляти в залишках основ А=(а₁,а₂,…,а_n), В=(b₁,b₂,…,b_n), при цьому n дорівнює кількості узятих основ-тобто трьом.

Результат будь-якої операції позначимо АВ =С, де С=(с₁,с₂,…,с_n). При цьому, 0<А<Р, 0<В<Р, 0<С<Р.

При виконанні операцій у СЗК, необхідно враховувати наступні особливості:

- між розрядами СЗК відсутні зв’язки;

- всі операції виконуються порозрядно і обчислення можна проводити паралельно;

- для кожного розряду СЗК використають малорозрядні суматори, що працюють по модулю р_і;

- є можливість використати замість суматорів прості таблиці результатів розрядів СЗК.

17.1 Додавання чисел у СЗК

Правило додавання двох чисел представлених у СЗК можна сформулювати в такий спосіб:

- числа складаються по розрядах основ, підсумуються їхні залишки;

- з отриманої суми залишків, віднімається основа цього розряду до одержання вирахування (залишку) результату цієї основи.

Формально це можна представити як: С=А+В, або (с₁,с₂,…,с_n) = (а₁,а₂,…,а_n)+(b₁,b₂,…,b_n), де кожний розряд дорівнює:

_{сі=(аі+bі)крі,}

де к=0, 1, 2  ціле число раз вирахування основи до одержання залишку.

Приклад 1. Нехай р₁=3, р₂=5, р₃=7, Р=105. Скласти числа А=67, В=13.

Рішення: Представимо числа в СЗК, де залишки записані в десятковій системі. Тоді А=67=(1,2,4), В=13=(1,3,6). Проведемо додавання по незалежних розрядах, тоді с₁=1+1=2 р₁= 3, тому с₁=2;

с₂=2+3=5=р₂, тому с₂=55=0;

с₃=4+6=107=р₃, тому с₃=107=3. Тоді:


А = 67 = (1,2,4)

+В = 13 = (1,3,6)

С = 80 = (2,0,3)

Приклад 2. Нехай р₁=7, р₂=9, р₃=11, р₄=13, р₅=17. Скласти десяткові числа.

Рішення:


А = 39031 = (6,7,3,5,16)

+В = 67556 = (6,2,5,8,15)

С= 106587 = (5,0,8,0,14)

Якщо залишки представити у двійковій системі числення, то і результат одержимо у двійковій системі.

17.2 Вирахування чисел у СЗК

Розглянемо операцію вирахування позитивних десяткових чисел за умови, що зменшуване більше від’ємника. Операція С=АВ реалізується порозрядно в такий спосіб:

_{сі=аіbі+крі,}

де к=0, якщо а_іb_і, і к=1, якщо а_іb_і.

Приклад 1. Нехай р₁=3, р₂=5, р₃=7, Р=105. Десяткові числа А=19=(1,4,5),

В=13 =(1,3,6). Потрібно вирахувати: С=А–В.

Рішення: с₁=1–1+0·3=0, с₂=4–3+0·5=1, с₃5–6+1·7=6. Тоді:


А = 19 = (1,4,5)

–В = 13 = (1,3,6)

С = 06 = (0,1,6).

Приклад 2. Нехай р₁=7, р₂=9, р₃=11, р₄=13, р₅=17, Р=153153. Десяткові числа А=67556=(6,2,5,8,15); В=39031=(6,7,3,5,16). Потрібно вирахувати: С=А–В.

Рішення:


А = 67556 = (6,2,5,8,15)

–В = 39031 = (6,7,3,5,16)

С = 28525 = (0,4,2,3,16)

17.3 Множення чисел у СЗК

Операція множення чисел у СЗК реалізується порозрядно множенням залишків з наступним відрахуванням К раз основи розряду до одержання залишку результату. Формальне множення

С=АВ реалізується за формулою:

_{сі = аі·bі – крі,}

де к =0,1,2…; р_і  і-та основа СЗК.

Приклад 1. Нехай р₁=3, р₂=5, р₃=7, Р=105. Помножити числа А=4, В=13.

Рішення. Представимо числа в СЗК: А=4=(1,4,4); В=13=(1,3,6).

Визначимо порозрядні добутки по кожній основі.

с₁ = 11=1, що менше р₁, тому с₁ = 1;

с₂ = 43=12 >25 , тому с₂=12–(25)=2;

с₃ = 46=24 >37, тому с₃=24–(37)=3.

Тоді, АВ=(1,4,4)(1,3,6)=(1,2,3)=52

Взявши ортогональні базиси В₁=70, В₂=21, В₃=15 (див. гл. 2.2), перевіримо: 70+221+315=157105=52.

Приклад 2. Нехай р₁=7, р₂=9, р₃=11, р₄=13, р₅=17, Р=153153. Помножити десяткові числа.

Рішення:


А = 407 = (1,2,0,4,16)

*В = 279 = (6,0,4,6,7)

С = 113553 = (6,0,0,11,10)

Самостійно визначити ортогональний базис і перевірити рішення.

17.4 Ділення чисел у СЗК

Операцію ділення будемо виконувати тільки із цілими позитивними числами, що мають цілу частку С. При цьому умови алгоритму операції ділення С =А/В наступні. Ділення виконується порозрядно у відповідності з формулою: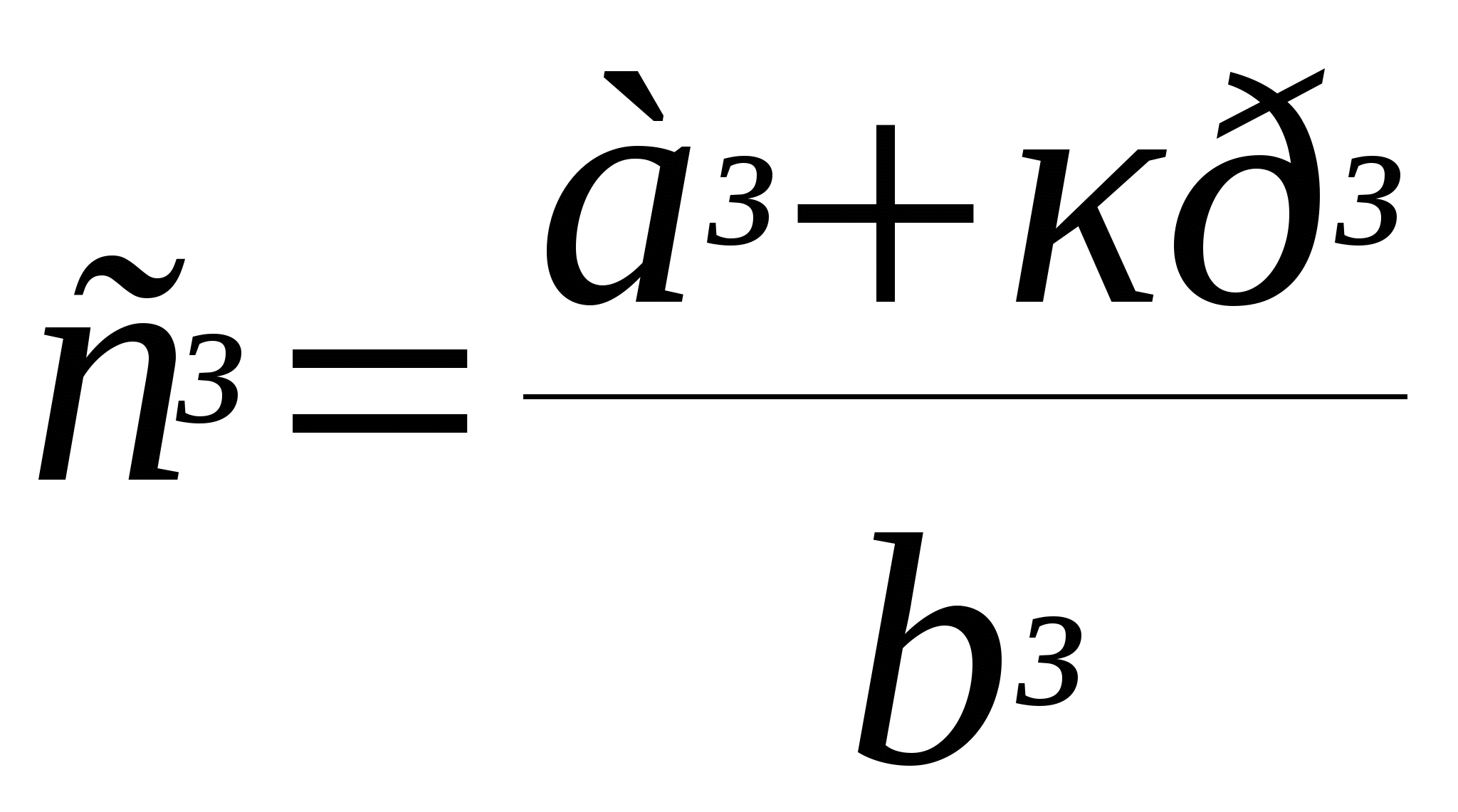

_,

де к=0,1,…,р_і–1.

При цьому, b≠0, а к вибирається так, щоб не було залишку при розподілі.

Приклад 1. Нехай р₁=3, р₂=5, р₃=7, Р=105. Необхідно розділити числа А=64, В=8.

Рішення. Запишемо числа в СЗК. А=64=(1,4,1); В=8=(2,3,1).

Визначимо порозрядні частки:

с₁ = (1+ к3)/2 = (1+13)/2 = 2 (к = 1);

с₂ = (4+ к5)/3 = (4+15)/3 = 3 (к = 1);

с₃ = (1+ к7)/1 = (1+07)/1 = 1 (к = 0). Тоді,


А = 64 = (1,4,1)

: В = 8 = (2,3,1)

С = 8 = (2,3,1)


Приклад 2. Нехай р₁=7, р₂=9, р₃=11, р₄=13, р₅=17. Розділити десяткові числа.

Рішення:


А = 18848 = (4,2,5,11,12)

: В = 152 = (5,8,9,9,16)

С = 124 = (5,7,3,7,5),

К = 3 6 2 4 4


Самостійно визначити ортогональний базис і перевірити рішення. Особливі випадки. Якщо b_і=0, то виникає невизначеність А/0. ЦА у цих випадках виробляє сигнал невизначеності і зупиняє рішення.

ПЕРЕЛІК ПОСИЛАННЬ

1. Бабич М.П., Жуков І.А. Комп`ютерна схемотехніка.-Київ.:МК-Прес, 2004.-412 с.: іл.

2. Буняк А. Електроніка та мікросхемотехніка.-Київ-Тернопіль: СМП «Астон», 2001.-382 с: іл.

3. Угрюмов Е. П. Цифровая схемотехника.- СПб.: БХВ – Санкт-Петербург, 2000. – 528 с.: ил.

4. Кудерметов Р.К., Щербаков А.М., Грушко С.С. Прикладна теорія цифрових автоматів. Навчальний посібник.-Запоріжжя, ЗНТУ, 2009.-190 с.: іл.

5. Савельев А. Я. Прикладная теория цифровых автоматов.-М. Высшая школа. 1987-272 с.

6. Акушский И.Я., Юдицкий Д. А. Машинная арифметика в остаточных классах. М. Высшая школа. 1968–453 с.

7. Глушков В. М. Синтез цифровых автоматов. М. Физматгиз. 1962– 475 с.

8. Евреинов Э. В., Бутыльский Ю. Т. Мамзелев И. А. и др. Цифровая и вычислительная техника. -М. Радио и связь. 1991.– 464 с.

9. Кудрявцев В. Б., Алешин С. В. Подколзин А. С. Введение в теорию автоматов. М. Наука. 1985– 320 с.

10. Кузин Л. Т. Основы кибернетики. Том1. М. Энергия. 1973–504 с.

11. Лихтциндер Б.Я., Кузнецов В. М. Микропроцессоры и вычислительные устройства в радиотехники.-К. Высшая школа. 1988–315 с.

12. Майоров С. А., Новиков Г. И., Немолочнов О. Ф. и др. Проектирование цифровых вычислительных машин. -М. Высшая школа. 1972– 345 с.

13. Поспелов Д. А. Логические методы анализа и синтеза схем. М. Энергия. 1974–368 с.

14. Поснов Н. Н. Арифметика вычислительных машин в упражнениях и задачах. Минск. Университетское. 1984–226 с.

15. Потемкин И. С. Функциональные узлы цифровой автоматики. М. Энергоатомиздат 1988 –320 с.

16. Савельев А. Я. Арифметические и логические основы цифровых автоматов. -М. Высшая школа, 1980–255 с.

17. Савельев А. Я. Основы информатики. -М. Высшая школа. 1991–235 с.

18. Соловьев В. В. Проектирование цифровых систем на основе программируемых логических интегральных схем. М. Горячая линия. 2001–636 с.

19. Самофалов К. Г. Цифровые ЭВМ. Практикум.-К. Высшая школа. 1989.

20. Самофалов К. Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов.-К. Вища школа. 1987-376 с.

21. Шеннон К. Э. Работы по теории информации и кибернетике.-М. Иностранная литература. 1963–830 с.