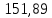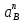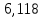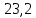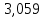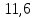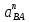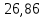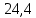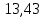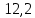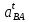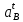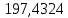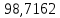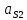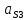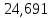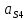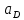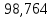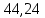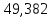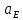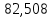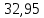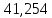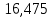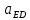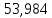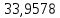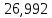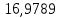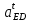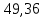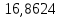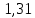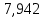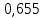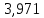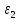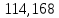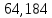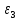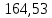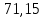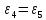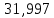Пояснительная записка курсовой работе по ТММ. Синтез и анализ механизмов
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
1.3.2. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК И ЗВЕНЬЕВ МЕХАНИЗМА Перейдем к определению ускорений положения 2. Ускорение точки А направлено по кривошипу AO от точки A к точке O и вычисляется по формуле: 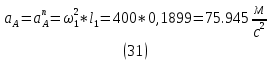 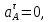 т.к. ε = 0, поскольку ω1 = const. т.к. ε = 0, поскольку ω1 = const.Ускорение точки B определяется из уравнения: 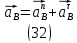 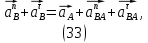 где 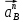 параллельно ВС, параллельно ВС, 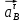 перпендикулярно ВС. Ускорение перпендикулярно ВС. Ускорение 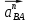 на плане ускорений строим параллельно АВ. на плане ускорений строим параллельно АВ.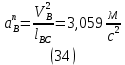 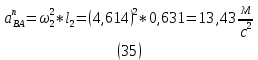 Для решения уравнения выбираем масштаб ускорения 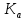 (м/с2 *мм) и вычисляем отрезки: (м/с2 *мм) и вычисляем отрезки: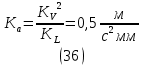 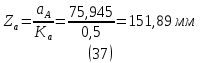 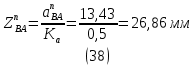 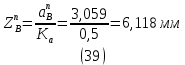 Из произвольно взятой точки о' , проводим отрезок  || АО в сторону О. Из его конца откладываем отрезок || АО в сторону О. Из его конца откладываем отрезок  ||ВА в сторону А и через его конец чертим прямую перпендикулярную звену АВ. Наконец из точки о' откладываем отрезок ||ВА в сторону А и через его конец чертим прямую перпендикулярную звену АВ. Наконец из точки о' откладываем отрезок 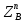 ||ВС в сторону С, а через его конец-прямую, перпендикулярную ВС. Пересечение проведенных прямых дает точку b', которая обозначает длины отрезков ||ВС в сторону С, а через его конец-прямую, перпендикулярную ВС. Пересечение проведенных прямых дает точку b', которая обозначает длины отрезков 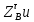 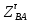 . Определяющих в масштабе . Определяющих в масштабе 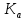 тангенциальные составляющие: тангенциальные составляющие: 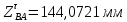 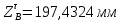 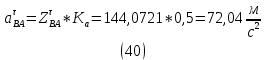  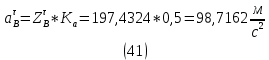 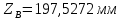 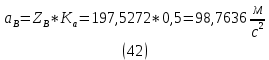 Ускорение точки D: 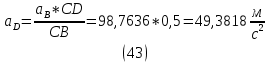 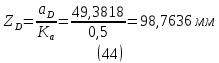 Найдем направление ускорения точки D. 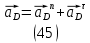 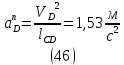 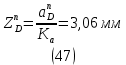 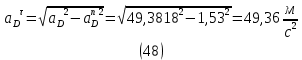 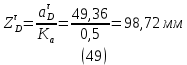 По полученным 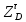 и и 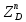 находим направление находим направление 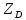 Ускорение точки E определяется из двух уравнений: 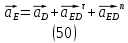 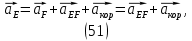 так как 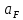 =0 =0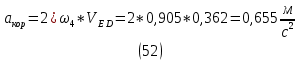 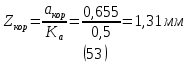 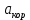 направлено перпендикулярно направлено перпендикулярно 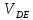 в сторону направления в сторону направления 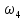 . .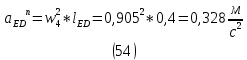 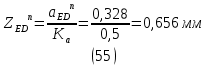 Приступаем к графическому решению уравнений по нахождению ускорения точки E. Для этого от точки d’ откладываем отрезок  || ED в сторону точки D, а через его конец – прямую, перпендикулярную ED. Затем из точки o’ проводим отрезок || ED в сторону точки D, а через его конец – прямую, перпендикулярную ED. Затем из точки o’ проводим отрезок  || || 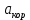 и через его конец проводим прямую || ED. Пересечение указанных прямых дает точку e’, которая определяет отрезки и через его конец проводим прямую || ED. Пересечение указанных прямых дает точку e’, которая определяет отрезки 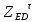 , , 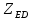 , и , и 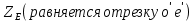 следовательно, ускорения следовательно, ускорения 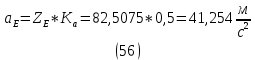 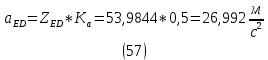 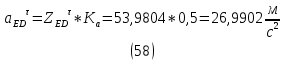 Найдем ускорения центров масс отрезков: 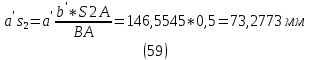 Графически находим 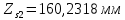 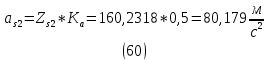 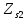 - это о’s2 на плане ускорений. - это о’s2 на плане ускорений. Найдем ускорение точки 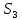 : :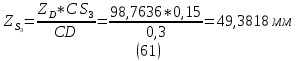 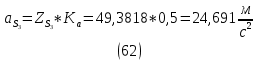 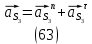 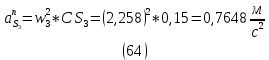 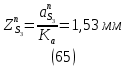 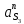 направлено по прямой C направлено по прямой C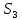 в сторону точки C. в сторону точки C.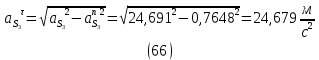 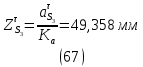 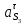 направлено перпендикулярно направлено перпендикулярно 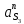 . .Через сумму векторов 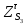 и и 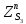 графически обозначили направление графически обозначили направление 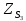 . . Ускорение точки 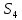 : :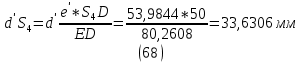 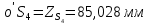 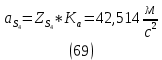 Для данного положения по следующим формулам определим угловые ускорения звеньев: 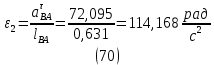 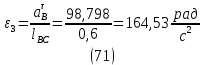 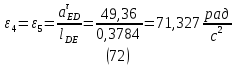 Определим ускорения точек и звеньев механизма и построим план ускорений для положения 6 в масштабе  = 0,5. = 0,5.Согласно уравнениям (32) – (72), описанным выше, находим ускорения точек и центров масс, угловые ускорения звеньев: ускорение точки А параллельно ОА и вычисляется по формуле:  = 76 м/с2 = 76 м/с2  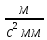 Ускорение точки B определяется из формул (32) – (33): 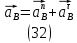 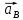 = = 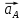 + + 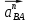 + + 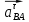 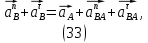 где 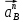 параллельно ВС, параллельно ВС, 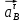 перпендикулярно ВС. Ускорение перпендикулярно ВС. Ускорение 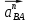 на плане ускорений строим параллельно АВ. на плане ускорений строим параллельно АВ. 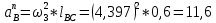 м/с2 м/с2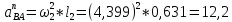 м/с2 м/с2Вычисляем отрезки в (мм): 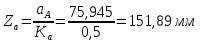 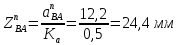 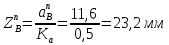 Из произвольно взятой точки о' , проводим отрезок 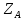 || АО в сторону О. Из его конца откладываем отрезок || АО в сторону О. Из его конца откладываем отрезок 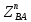 ||ВА в сторону А и через его конец чертим прямую перпендикулярную звену АВ . Наконец из точки о' откладываем отрезок ||ВА в сторону А и через его конец чертим прямую перпендикулярную звену АВ . Наконец из точки о' откладываем отрезок 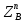 ||ВС в сторону С, а через его конец – прямую, перпендикулярную ВС. ||ВС в сторону С, а через его конец – прямую, перпендикулярную ВС. Пересечение проведенных прямых дает точку b', которая обозначает длины отрезков 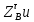 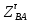 . Проведем из точки o’ отрезок к точке b’. Найдем таким образом . Проведем из точки o’ отрезок к точке b’. Найдем таким образом 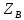 . . 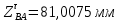 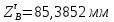 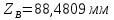 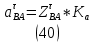 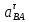 = = 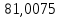 * * 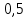 = 40,5 м/с2 = 40,5 м/с2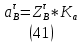 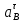 = =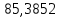 * * 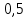 = 42,69 м/с2 = 42,69 м/с2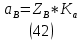 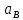 = = 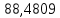 * * 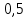 = 44,24 м/с2 = 44,24 м/с2 Ускорение точки D: 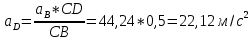 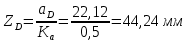 Найдем направление ускорения точки D. 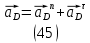 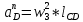 = =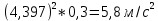 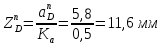 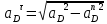 = =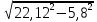 =21,3461 =21,3461 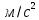 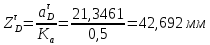 По полученным 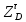 и и 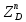 находим направление находим направление 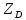 Ускорение точки E определяется из уравнений (50) – (51): 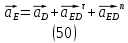 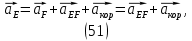 так как 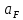 =0 =0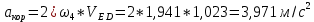 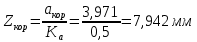 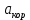 направлено перпендикулярно направлено перпендикулярно 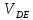 в сторону направления в сторону направления 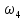 . .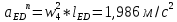 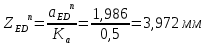 Приступаем к графическому решению уравнений по нахождению ускорения точки E. Для этого от точки d’ откладываем отрезок 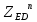 || ED в сторону точки D, а через его конец – прямую, перпендикулярную ED. Затем из точки o’ проводим отрезок || ED в сторону точки D, а через его конец – прямую, перпендикулярную ED. Затем из точки o’ проводим отрезок 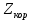 || || 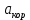 и через его конец проводим прямую || ED. Пересечение указанных прямых дает точку e’, которая определяет отрезки и через его конец проводим прямую || ED. Пересечение указанных прямых дает точку e’, которая определяет отрезки 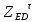 , , 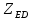 , и , и 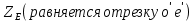 следовательно, ускорения следовательно, ускорения 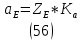 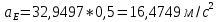 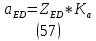 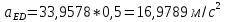 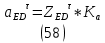 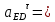 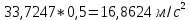 Найдем ускорения центров масс звеньев: 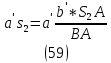 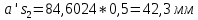 Графически находим 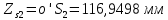 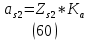 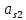 = = 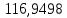 * * 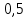 = 58,4749 м/с2 = 58,4749 м/с2Найдем ускорение точки 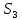 : :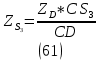 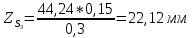 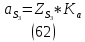 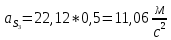 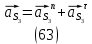 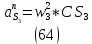 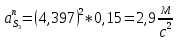 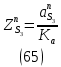 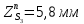 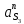 направлено по прямой C направлено по прямой C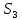 в сторону точки C. в сторону точки C.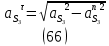 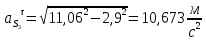 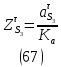 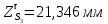  направлено перпендикулярно направлено перпендикулярно 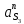 . .Через сумму векторов 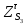 и и 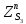 графически обозначим направление графически обозначим направление 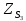 . . Ускорение точки 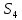 : :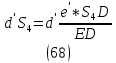 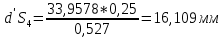 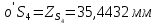 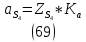 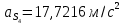 Для данного положения по следующим формулам определим угловые ускорения звеньев: 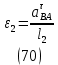 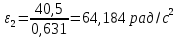 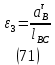  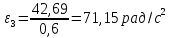 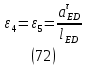 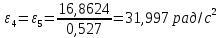 Таблица 3 – Результаты вычислений ускорений точек.
Таблица 4 – Результаты вычислений угловых ускорений звеньев.
1.3.3. ОПРЕДЕЛЕНИЕ РАДИУСОВ КРИВИЗНЫ Далее определим радиус кривизны точки 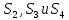 в положении 2 и для этого воспользуемся следующей формулой: в положении 2 и для этого воспользуемся следующей формулой: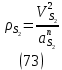 Радиус кривизны точки 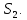 Для определения составляющей 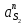 через начало вектора через начало вектора 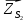 , взятого с плана ускорений, проводим прямую, параллельную отрезку os на плане скоростей. Из конца вектора , взятого с плана ускорений, проводим прямую, параллельную отрезку os на плане скоростей. Из конца вектора 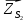 опускаем перпендикулярно на эту прямую и получаем вектор опускаем перпендикулярно на эту прямую и получаем вектор 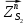 , следовательно, и составляющую , следовательно, и составляющую 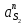 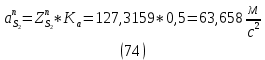 Следовательно: 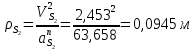 Чтобы показать центр кривизны, найдём отрезок (мм) 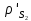 = = 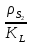 и отложим его от точки S2 параллельно и отложим его от точки S2 параллельно 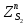 в сторону направления этого вектора: в сторону направления этого вектора: Радиус кривизны точек  , ,  (аналогично уравнениям (73) – (75)). (аналогично уравнениям (73) – (75)).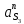 = = 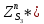 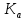 = 1,544* 0,5 =0,772 м/с2 = 1,544* 0,5 =0,772 м/с2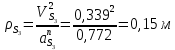 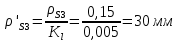 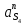 = = 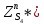 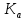 = 1,9214* 0,5 =0,9607 м/с2 = 1,9214* 0,5 =0,9607 м/с2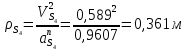 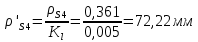 Радиусы кривизны точек для положения 6: Радиус кривизны точки 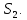 Все действия, выполненные для нахождения радиусов кривизны для положения 2, аналогичны для нахождения радиусов кривизны для положения 6. Следовательно, пользуемся уравнениями (73) – (75). Все действия, выполненные для нахождения радиусов кривизны для положения 2, аналогичны для нахождения радиусов кривизны для положения 6. Следовательно, пользуемся уравнениями (73) – (75).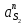 = = 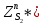 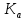 = 102,1193* 0,5 =51,06 м/с2 = 102,1193* 0,5 =51,06 м/с2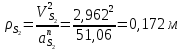 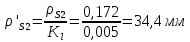 Радиус кривизны точки 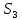 . .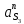 = = 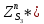 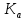 = 5,8 * 0,5 =2,9 м/с2 = 5,8 * 0,5 =2,9 м/с2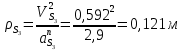 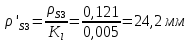 Радиус кривизны точки 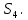 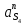 = = 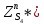 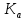 = 10,2557* 0,5 =5,1279 м/с2 = 10,2557* 0,5 =5,1279 м/с2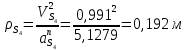 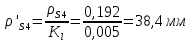 1.4 СИЛОВОЙ АНАЛИЗ Приступаем к силовому анализу механизма в 6-м положении. Для дальнейших расчетов нам необходимо рассчитать главные векторы и моменты сил, приложенных в каждом из рассматриваемых звеньев, по следующим формулам: 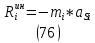 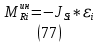 Согласно формулам (76) и (77): 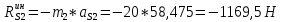 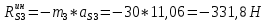 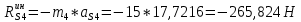 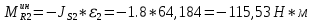 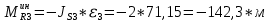 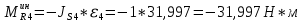 Найдем силы тяжести, действующие на звенья: 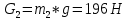 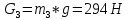 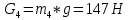 Силовой анализ механизма проведем, начиная с наиболее удаленной от входного звена группы Ассура второго класса, представленной шатуном 4 и кулисой 5 (ВПВ). Найдем величины 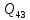 и и 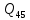 . Для этого составим уравнение равновесия моментов сил относительно точки D: . Для этого составим уравнение равновесия моментов сил относительно точки D: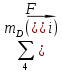 =0 =0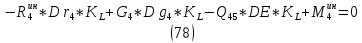 Откуда находим 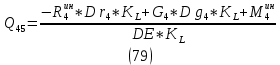 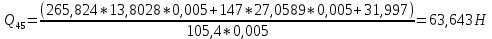 Составим уравнение равновесия сил, действующих на звено 4: 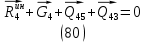 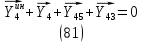 Построим план сил в масштабе 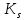 =5 H/мм откуда: =5 H/мм откуда: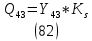 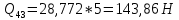 Теперь рассмотрим вторую группу Ассура: звенья 2-3 (2 – шатун, 3 – балансир). Группа Ассура вида (ВВВ). Найдем величины 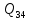 и и 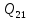 . . 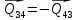 . Запишем уравнение равновесия моментов относительно точки B сил, приложенных к звену 2: . Запишем уравнение равновесия моментов относительно точки B сил, приложенных к звену 2: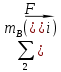 =0 =0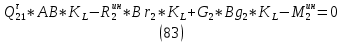 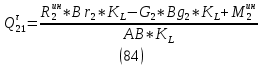 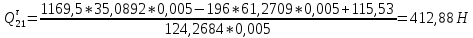 В точке С действуют реакции 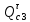 и и 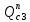 . Найдем . Найдем 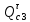 через уравнение равновесия моментов сил звена 3 относительно точки В: через уравнение равновесия моментов сил звена 3 относительно точки В: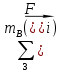 =0 =0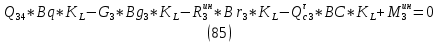 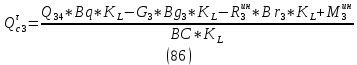 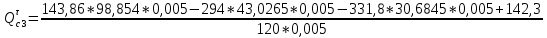 =165,419 H =165,419 HДля определения составляющих 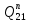 и и 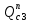 составим уравнение равновесия сил, приложенных к звеньям 2 и 3: составим уравнение равновесия сил, приложенных к звеньям 2 и 3: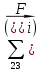 =0 =0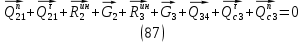 Построим план сил в масштабе 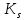 = 5 H/мм: = 5 H/мм: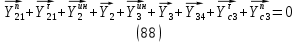 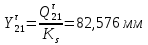 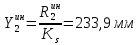 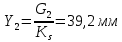 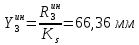 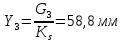 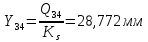 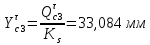 Тогда: 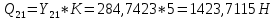 Рассмотрим равновесие входного звена – кривошипа, к которому в шарнире А приложена сила  и в шарнире О – сила и в шарнире О – сила  . Кроме того, к этому звену приложен внешний момент . Кроме того, к этому звену приложен внешний момент 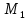 . Принимая во внимание, что (по условию задания) кривошип вращается с постоянной угловой скоростью относительно главной центральной оси инерции и поэтому . Принимая во внимание, что (по условию задания) кривошип вращается с постоянной угловой скоростью относительно главной центральной оси инерции и поэтому 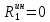 и и 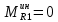 из уравнений равновесия сил и их моментов относительно точки A: из уравнений равновесия сил и их моментов относительно точки A: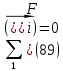 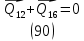 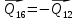 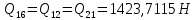 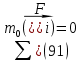 Также определим внешний момент 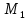 по следующей формуле: по следующей формуле: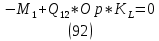 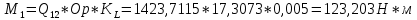 1.5 ОПРЕДЕЛЕНИЕ ВНЕШНЕГО (УРАВНОВЕШИВАЮЩЕГО) МОМЕНТА РЫЧАГОМ Н.Е. ЖУКОВСКОГО Начертим план скоростей для 6 положения, повернутый на 90 градусов. Представим момент 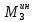 как пару сил, приложенных в точках B и C, момент как пару сил, приложенных в точках B и C, момент 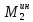 как пару сил, приложенных в точках А и В, момент как пару сил, приложенных в точках А и В, момент 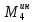 как пару сил, приложенных в точках Е и D (см. уравнение (93)). Параллельно перенесем все силы инерции и силы тяжести в соответствующие точки на плане скоростей. Далее запишем уравнение моментов относительно точки о и найдем, необходимую для расчета момента, силу как пару сил, приложенных в точках Е и D (см. уравнение (93)). Параллельно перенесем все силы инерции и силы тяжести в соответствующие точки на плане скоростей. Далее запишем уравнение моментов относительно точки о и найдем, необходимую для расчета момента, силу 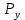 : :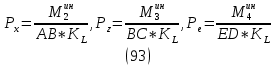 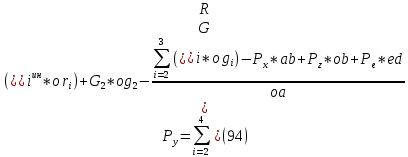 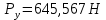 Следовательно, искомый момент равен: 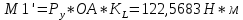 Тогда относительная погрешность равна: 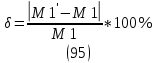 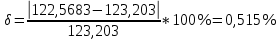 Расхождение результатов лежит в пределах допустимого (<5%). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||