Пример содержания отчета по лабораторной работе №6 «Решение однокритериальной статической задачи в условиях неопределенности при играх с противником»
Исходные данные:
Предприятие выпускает восемь видов товаров. Для производства указанных товаров используется 15 видов ресурсов. Рассматривалась проблема недостаточности дохода предприятия. Требуется определить программу производства товаров различного вида, обеспечивающую максимум среднего дохода предприятия. Параметры задачи представлены теми же числовыми данными, которые использовались при выполнении работы №2. Рассмотрена задача с одним неопределенным параметром  , принимающим только два возможных значения , принимающим только два возможных значения 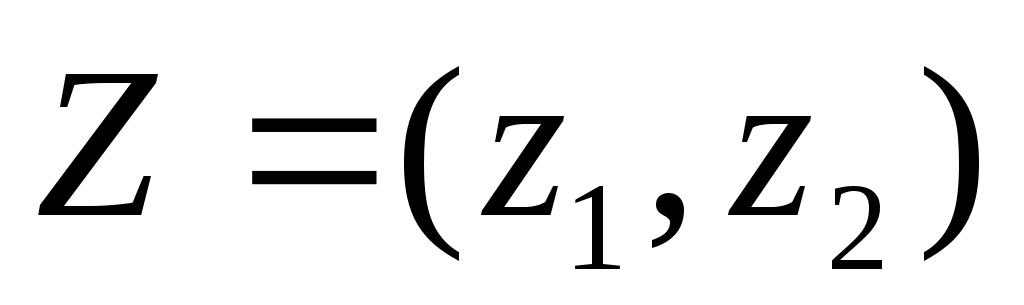 при выборе противником соответственно стратегий при выборе противником соответственно стратегий 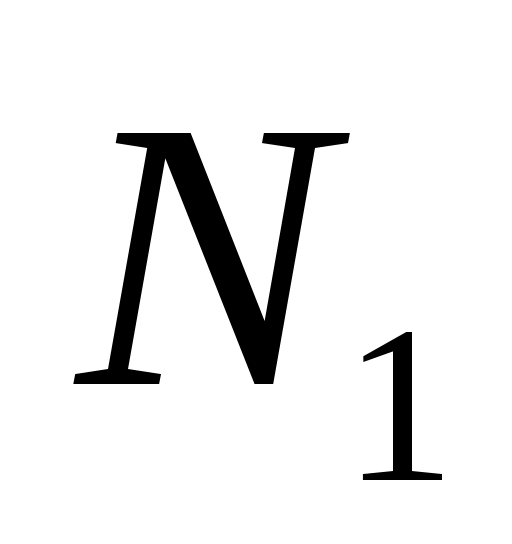 и и 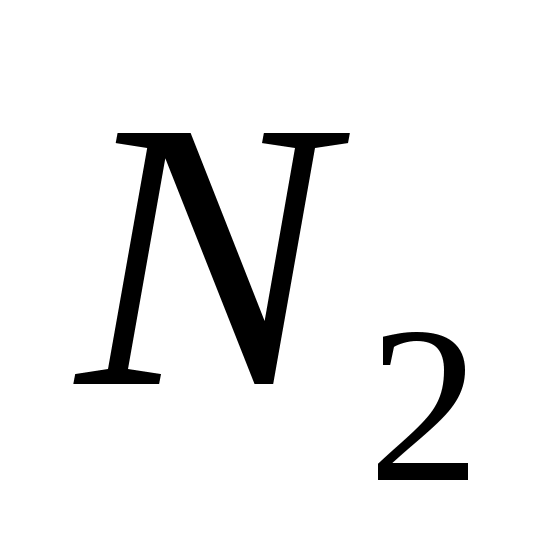 . Случайным параметром в условиях неопределенности принята цена товара 1. Предположено, что данных о законе распределения случайного параметра нет. Выдвинута гипотеза о том, что в результате возможных действий противника (конкурента) цена товара 1 может принимать два значения . Случайным параметром в условиях неопределенности принята цена товара 1. Предположено, что данных о законе распределения случайного параметра нет. Выдвинута гипотеза о том, что в результате возможных действий противника (конкурента) цена товара 1 может принимать два значения 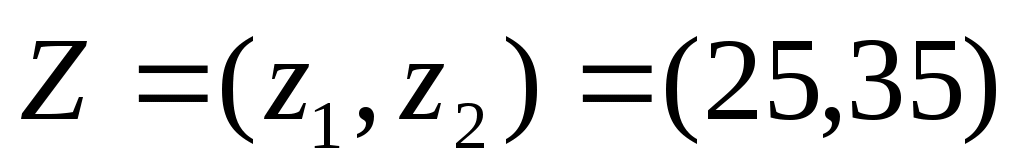 . .
Решение:
Найдены два оптимальных решения 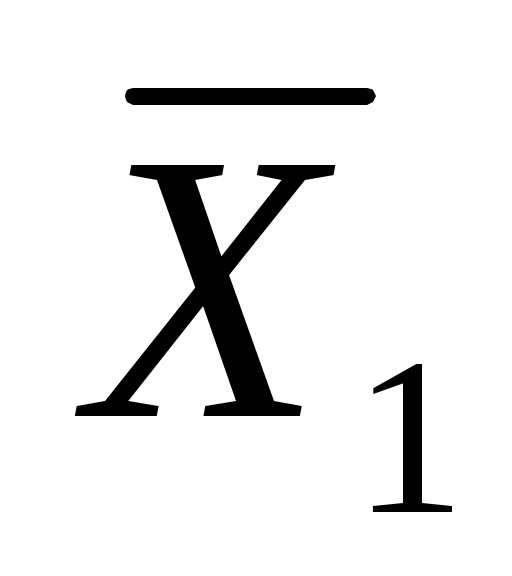 и и 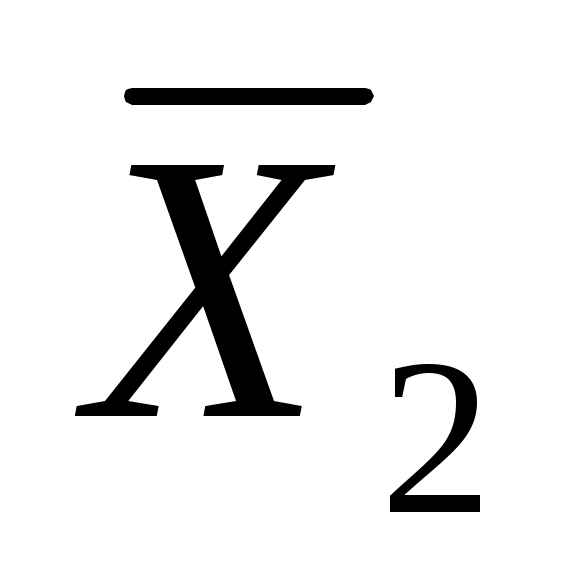 , с учетом двух возможных и предполагаемых нами стратегий противника , с учетом двух возможных и предполагаемых нами стратегий противника 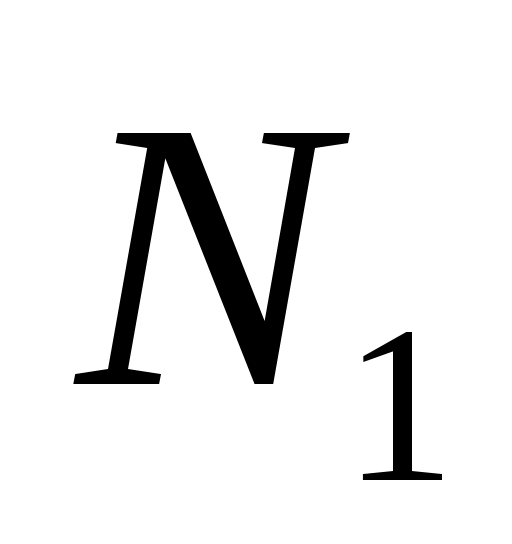 и и 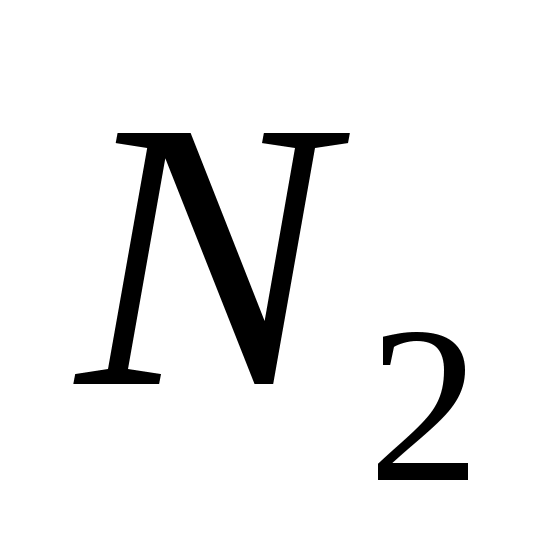 соответствующие выражениям соответствующие выражениям
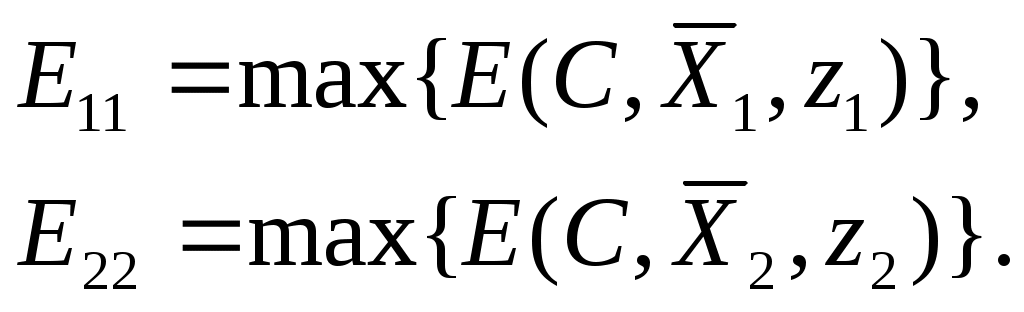
Полученные решения 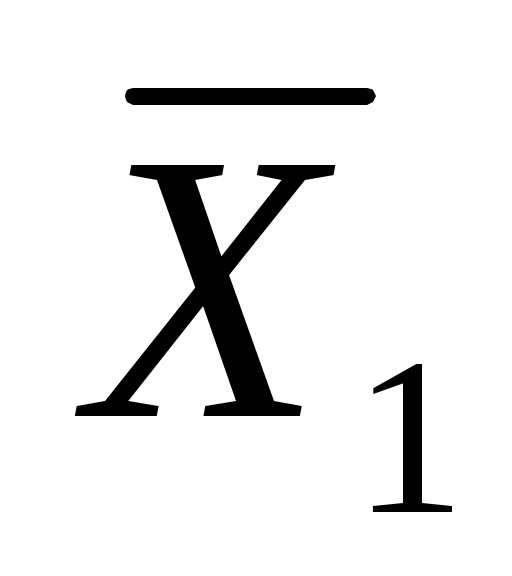 и и 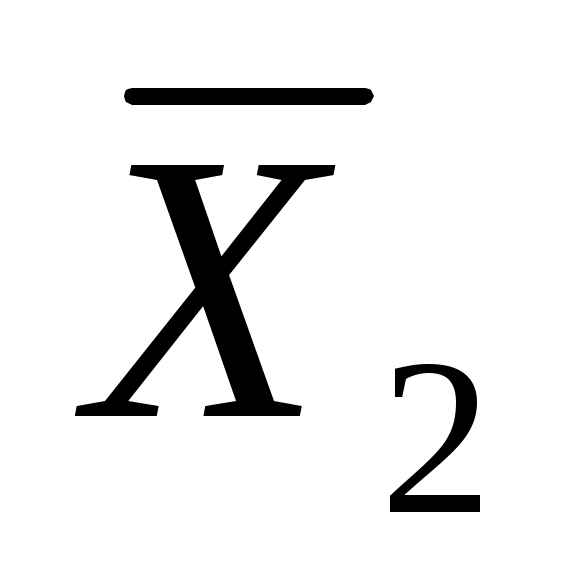 представляют собой наши оптимальные действия (стратегии) представляют собой наши оптимальные действия (стратегии) 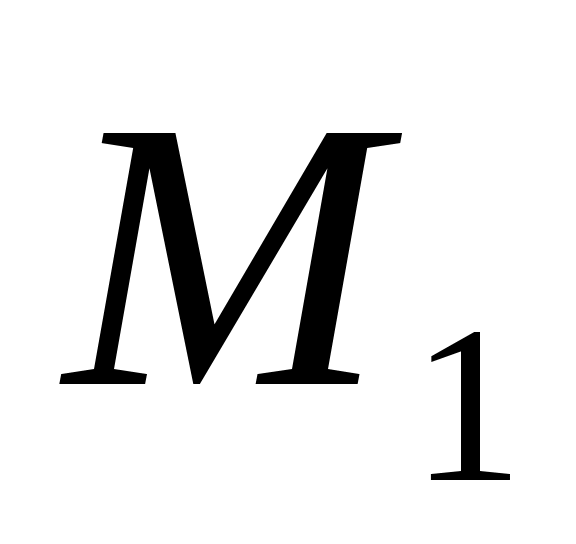 и и 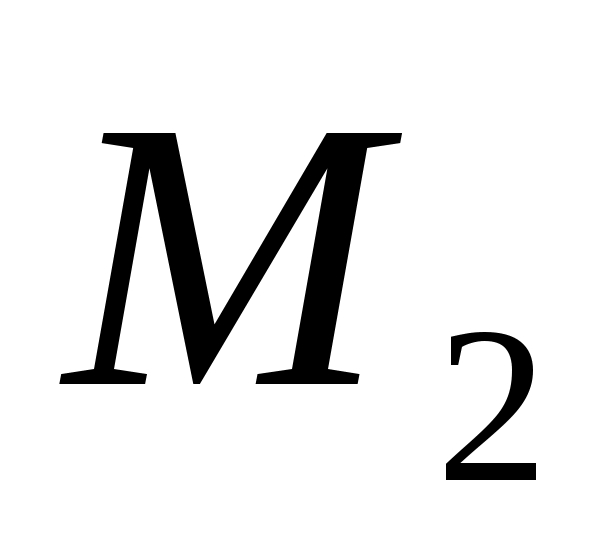 в том случае, когда мы угадали дальнейшее развитие событий. Решение с ценой в том случае, когда мы угадали дальнейшее развитие событий. Решение с ценой 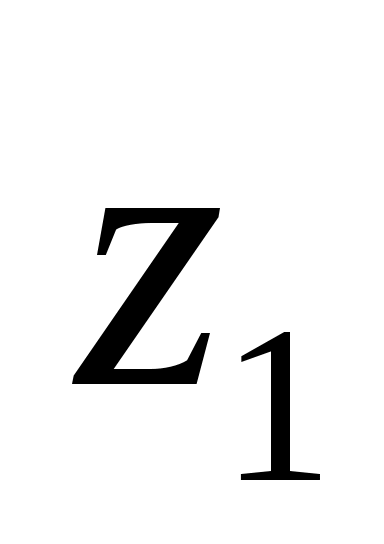 представлено в таблице П19. представлено в таблице П19.
Таблица П19. Решение 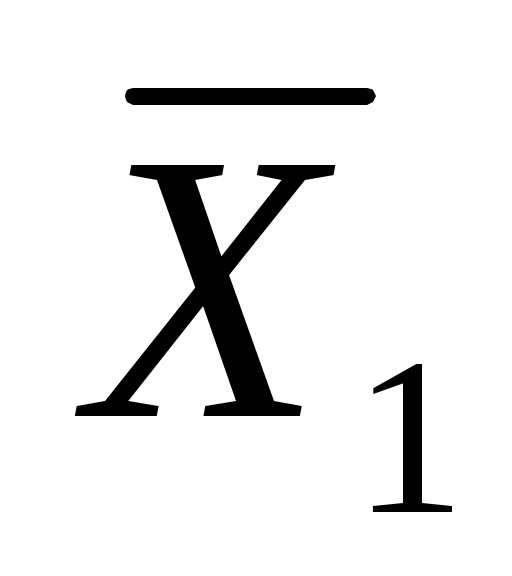 при при 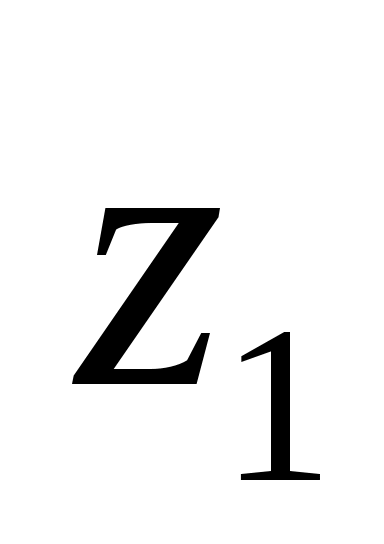
Товары
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Доход
|
Количество (шт.)
|
13,93127
|
3,200906
|
0
|
5,386733
|
0,599527
|
0
|
20,1504
|
0
|
Цена
|
25
|
23
|
10
|
22
|
18
|
19
|
24
|
20
|
1034,812
|
Решение с ценой 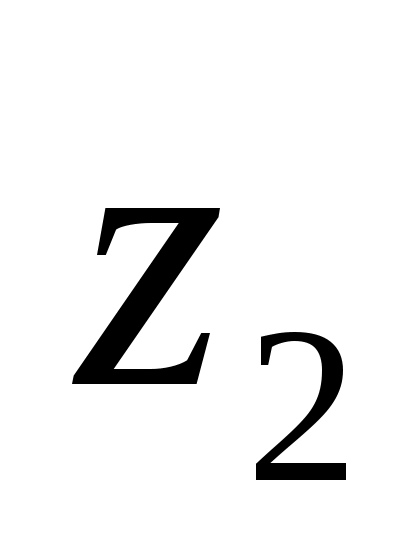 представлено в таблице П20. представлено в таблице П20.
Таблица П20. Решение 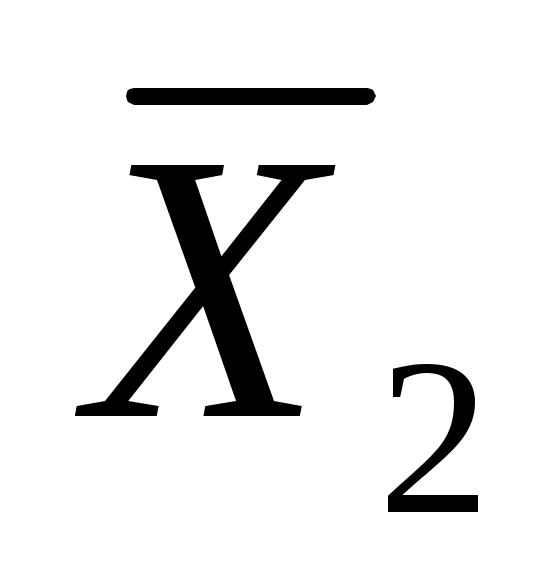 при при 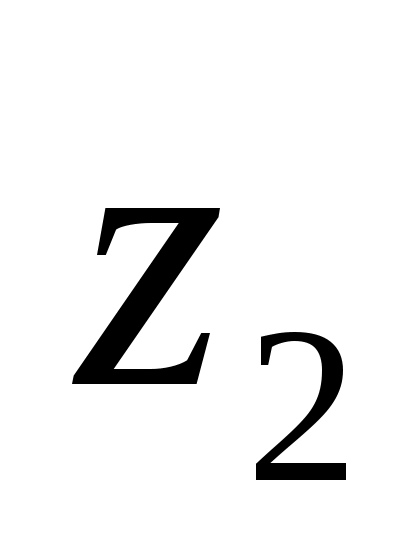
Товары
|
Товар 1
|
Товар 2
|
Товар 3
|
Товар 4
|
Товар 5
|
Товар 6
|
Товар 7
|
Товар 8
|
Доход
|
Количество (шт.)
|
35,60091
|
2,721088
|
0
|
2,947846
|
0
|
0
|
0
|
0
|
Цена
|
35
|
23
|
10
|
22
|
18
|
19
|
24
|
20
|
1373,469
|
Рассчитаны значения показателя эффективности при условии, что мы не угадали ответ противника
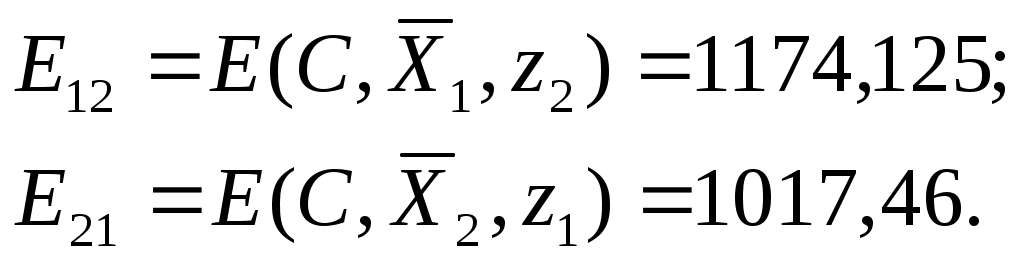
Таким образом, рассчитаны все элементы  платежной матрицы (таблица П21), где строки платежной матрицы (таблица П21), где строки 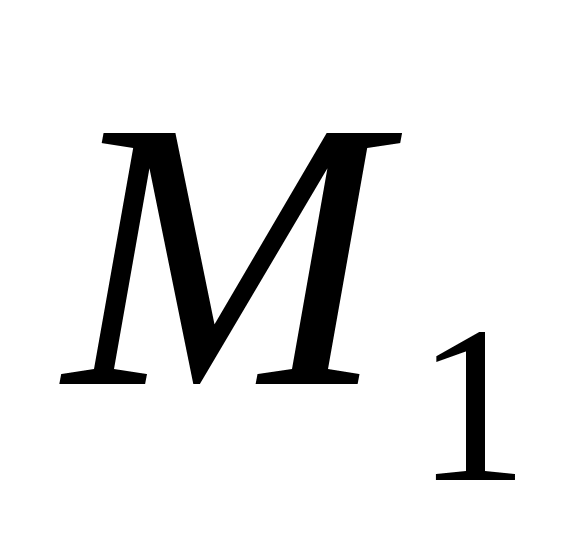 и и 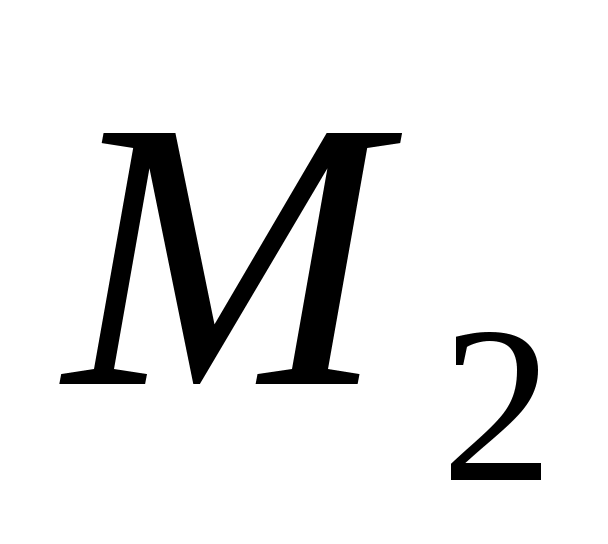 представляют собой наши возможные стратегии, а столбцы представляют собой наши возможные стратегии, а столбцы 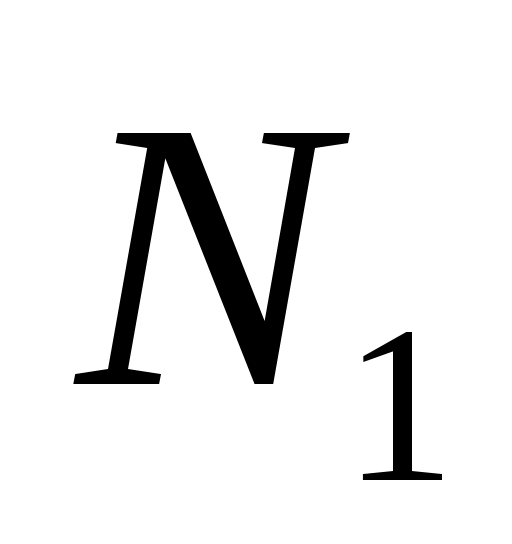 и и 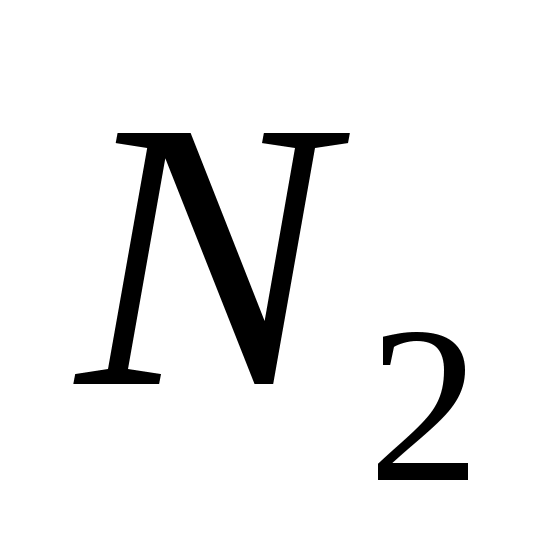 возможные стратегии противника, и отдельно записаны соответствующие им решения возможные стратегии противника, и отдельно записаны соответствующие им решения 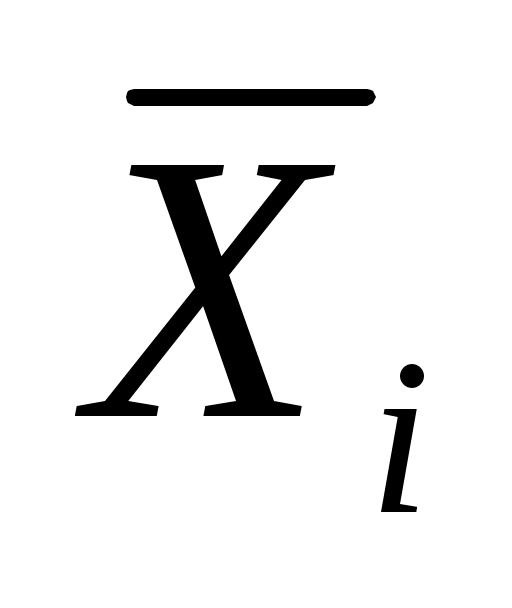 : :
Таблица П21. Платежная матрица задачи при играх с противником
Стратегии
|
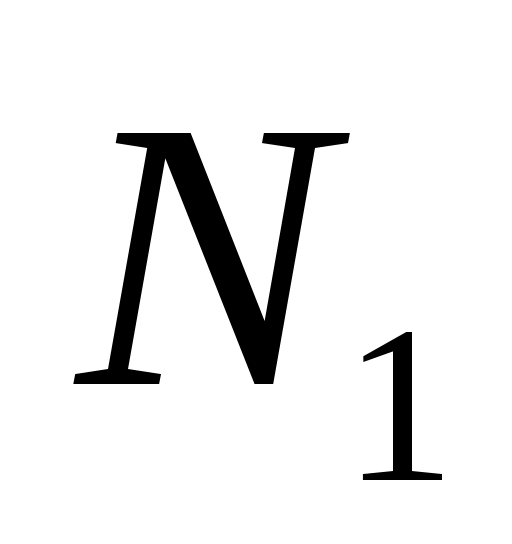
|
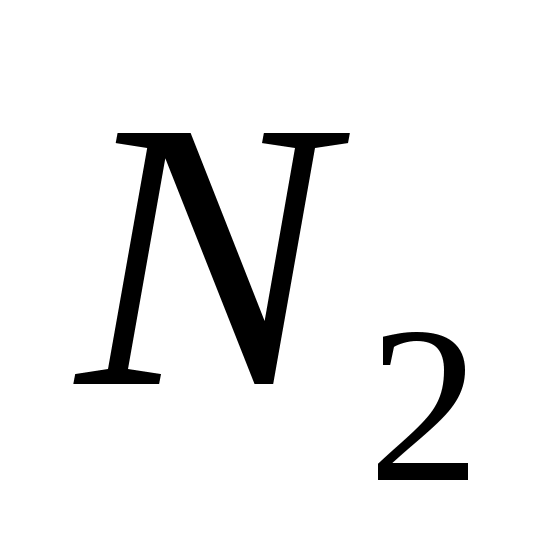
|
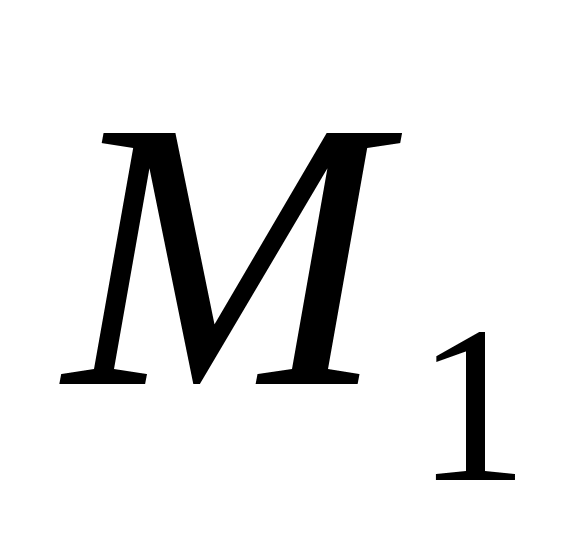
|
1034,812
|
1174,125
|
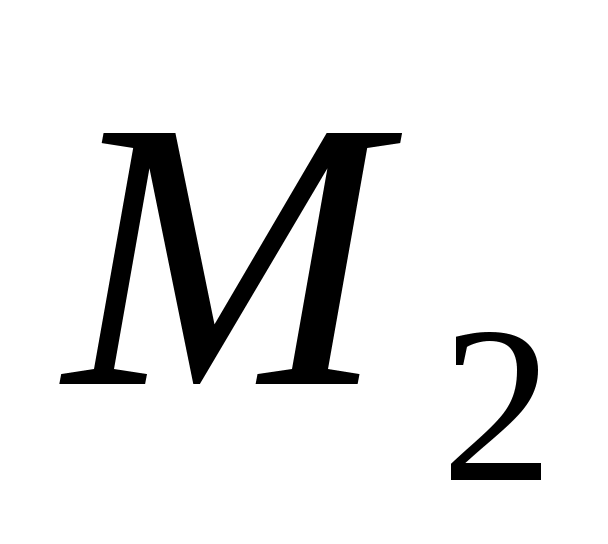
|
1017,46
|
1373,469
|
Обозначим 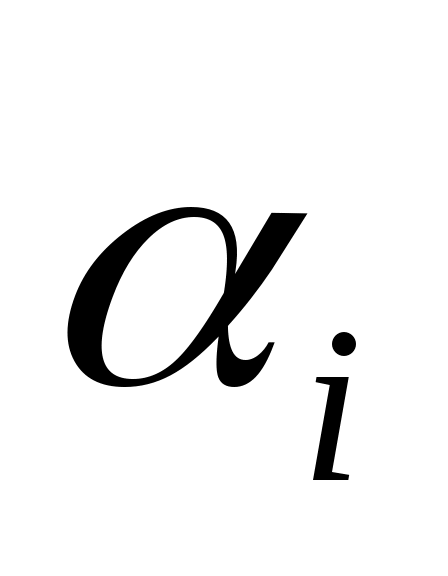 минимальный выигрыш при выборе стратегии минимальный выигрыш при выборе стратегии 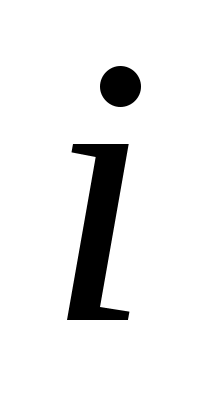 при всех возможных стратегиях противника при всех возможных стратегиях противника
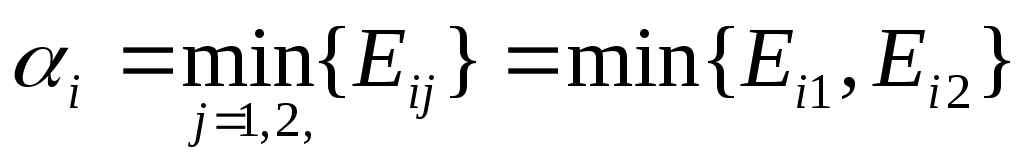 . .
По стратегии 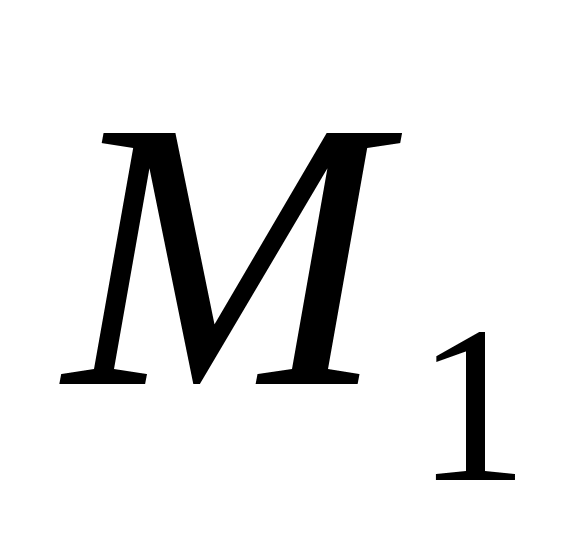 минимальный выигрыш составит минимальный выигрыш составит 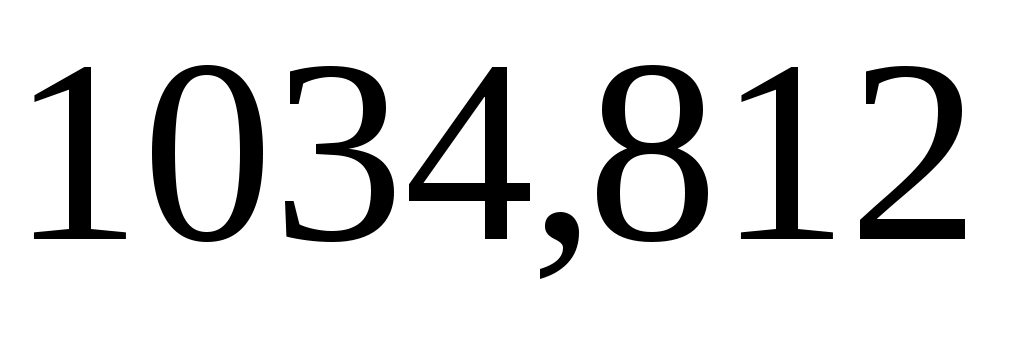 , а по стратегии , а по стратегии 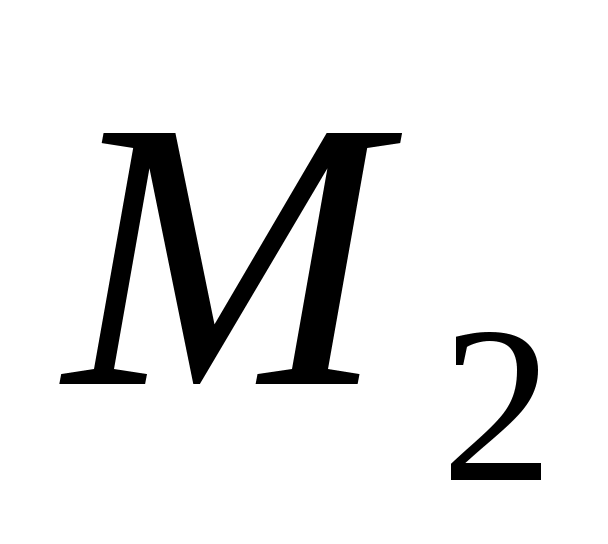 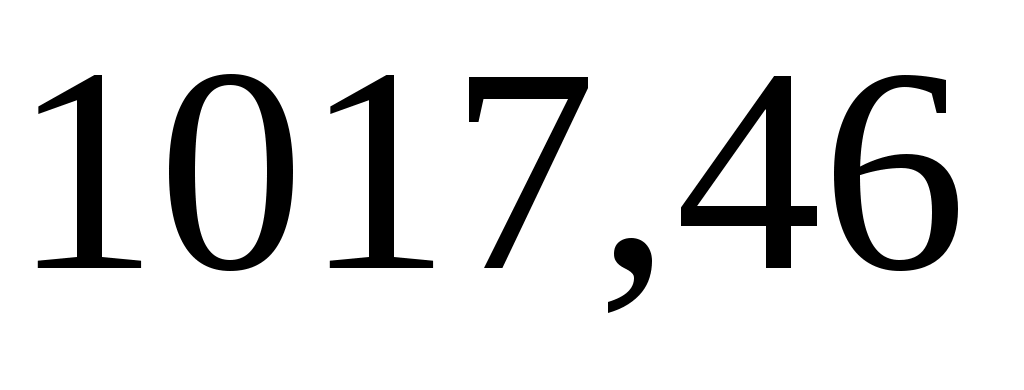 . .
Из возможных наших стратегий по критерию Вальда (критерий "крайнего пессимизма) выбрана стратегия, которая обеспечивает нам наибольшее значение нашего минимального выигрыша:
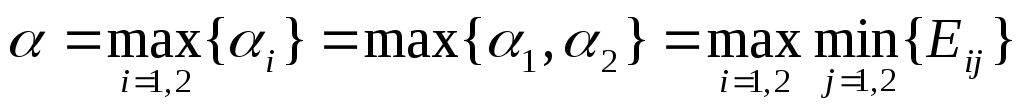 . .
Очевидно, что это будет стратегия 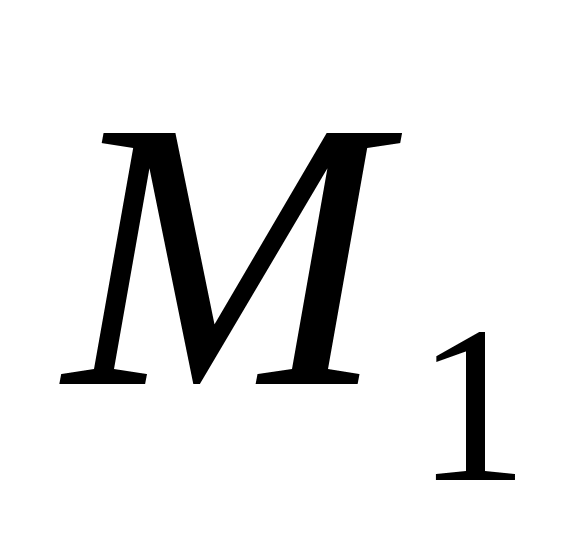 .Нижняя цена игры .Нижняя цена игры 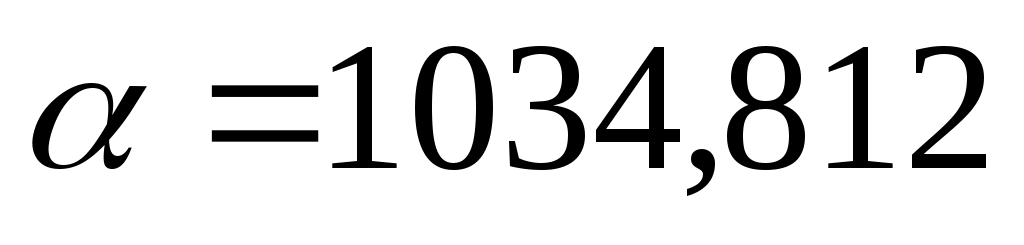 (наш гарантированный выигрыш при любой стратегии противника). (наш гарантированный выигрыш при любой стратегии противника).
В предположении, что противник вооружен теми же знаниями, которые использовали мы, определена наилучшая стратегия для него. Поскольку имеет место дуальная игра, наш выигрыш есть проигрыш противника.
Найден наш максимальный выигрыш при каждой стратегии противника
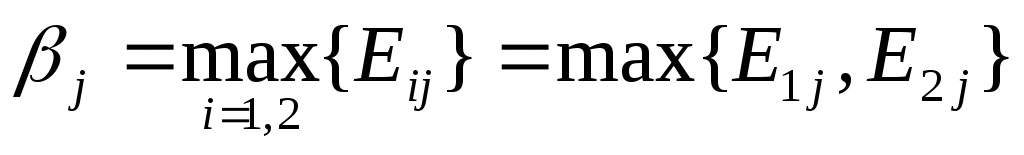 . .
По стратегии 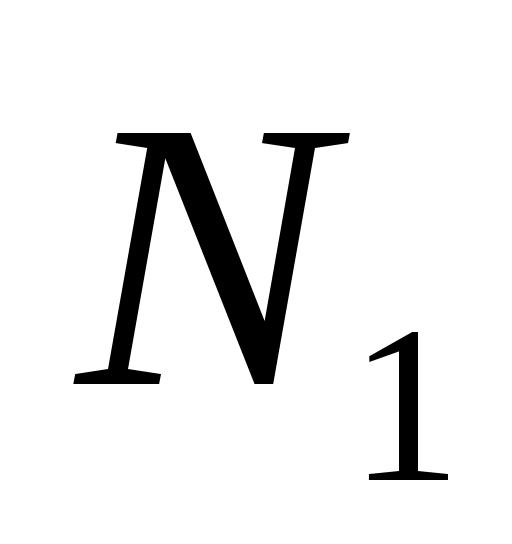 максимальный выигрыш составит максимальный выигрыш составит 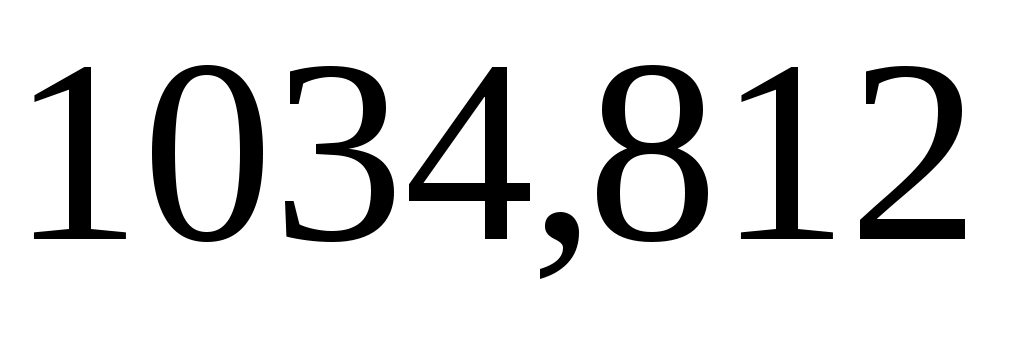 , а по стратегии , а по стратегии 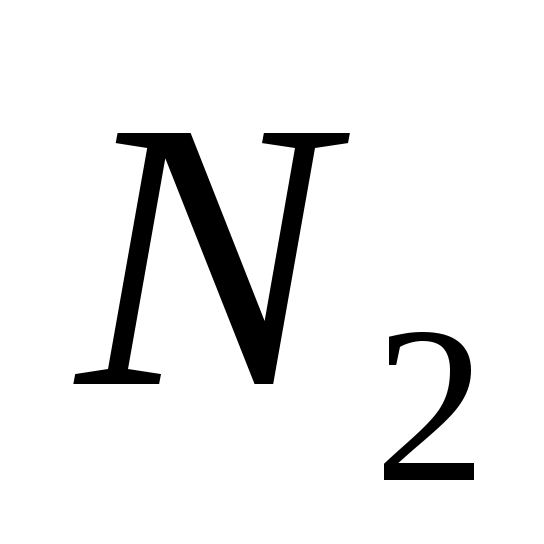 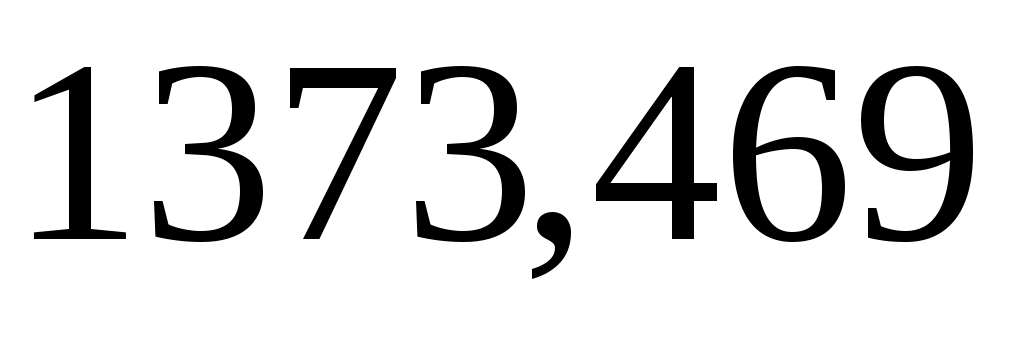 . Для того, чтобы минимизировать свой проигрыш, противник выберет стратегию, в которой наш выигрыш минимален: . Для того, чтобы минимизировать свой проигрыш, противник выберет стратегию, в которой наш выигрыш минимален:
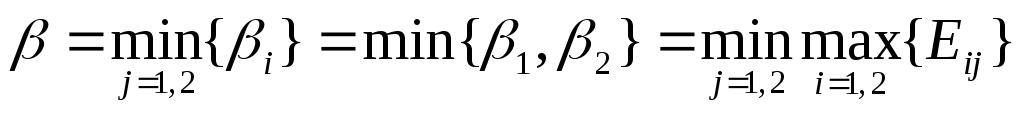 . .
Очевидно, что это будет стратегия 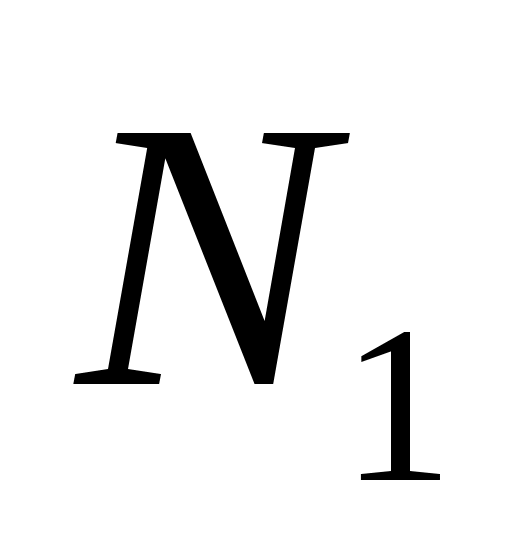 . Назовем выигрыш . Назовем выигрыш 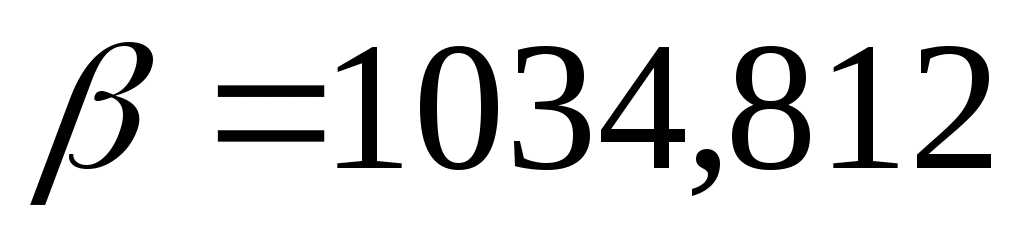 верхней ценой игры. Верхняя и нижняя цены игры совпадают, то есть мы получили чистую цену игры верхней ценой игры. Верхняя и нижняя цены игры совпадают, то есть мы получили чистую цену игры 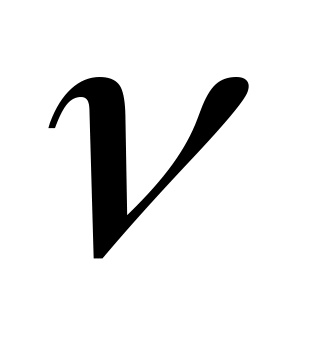 : :
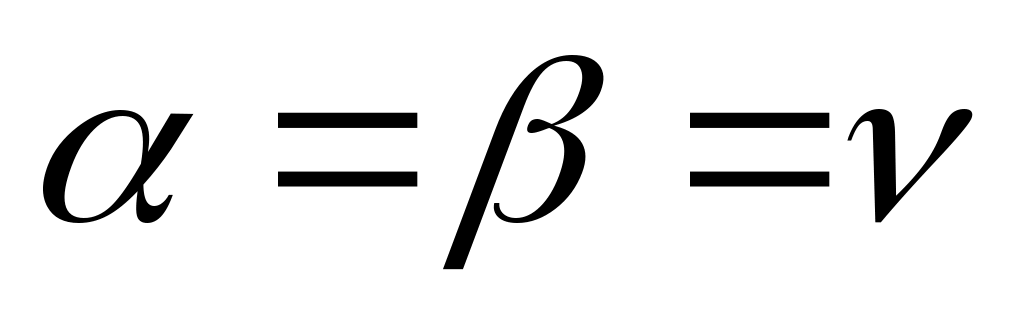 . .
Стратегии, соответствующие чистой цене игры, называются чистыми, а их совокупность дает оптимальное решение. Используя оптимальное решение, мы получаем минимальный гарантированный выигрыш  независимо от поведения противника. Пара чистых стратегий независимо от поведения противника. Пара чистых стратегий 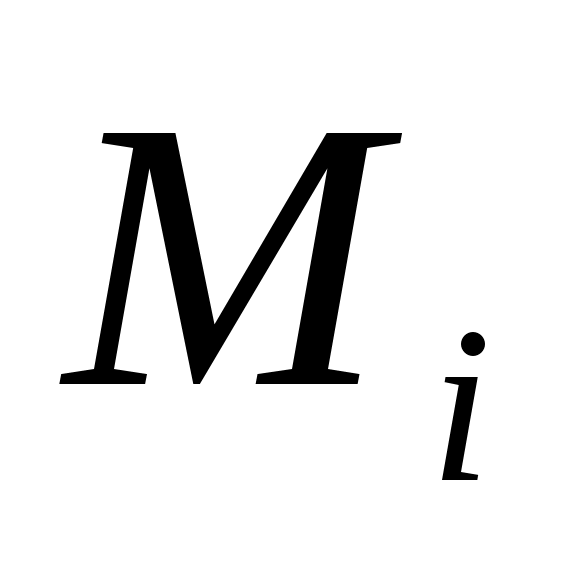 и и  дает оптимальное решение игры тогда и только тогда, когда соответствующий им элемент дает оптимальное решение игры тогда и только тогда, когда соответствующий им элемент  является одновременно наибольшим в своем столбце и наименьшим в своей строке. Таким образом, имеется седловая точка. является одновременно наибольшим в своем столбце и наименьшим в своей строке. Таким образом, имеется седловая точка.
Выводы:
Решение задачи соответствует стратегии 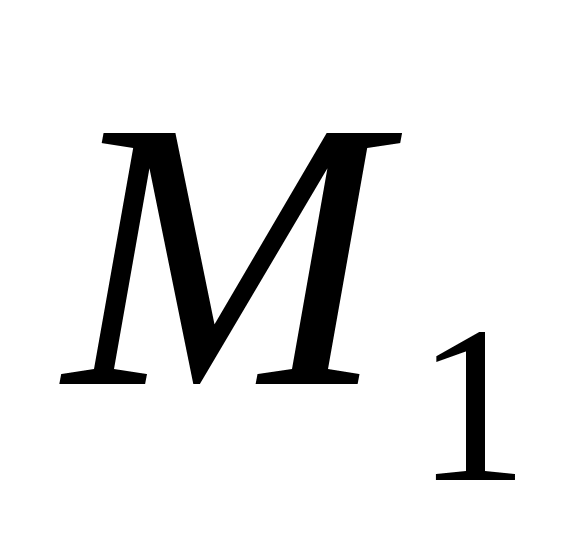 и дает оптимальное решение {13,93; 3,20; 0; 5,39; 0,56; 0; 20,15; 0}. и дает оптимальное решение {13,93; 3,20; 0; 5,39; 0,56; 0; 20,15; 0}.
|
 Скачать 3.85 Mb.
Скачать 3.85 Mb.