Система счисление. Системы счисления. Системы счисления

• Название: Системы счисления
• Анкор: Система счисление
• Дата: 07.06.2022
• Размер: 0.51 Mb.
• Имя файла: Системы счисления.doc
• Тип: Практикум; #576502
• страница: 4 из 4

Выполните указанные действия

1) 100101₂*101₂= 6) 11001,1₂*11,01₂= 2) 100001₂+10010₂= 7) 101101₂*111₂=

3) 1110101010₂[phone]₂ = 8) 10111010₂[phone]₂ =

4) 111101110,1011₂+1111011110,1₂ = 9) 101₂+101₂=

5) 111101₂*1010111₂ = 10) 110001₂+1011₂=

Упражнения для самоподготовки
Задание №1. Запишите числа в развернутой форме

1) 101, 01₂ 4) 673,2₈ 7) 8А,F_1б 10) 19,99₁₀ 13) 10,10₂

2) 64,5₈ 5) 39,F₁₆ 8) 755₈ 11) ВС₁₆ 14) 7764,1₈

3) 2430,43₅ 6) 3AF,15₁₆ 9) 1011,01₂ 12) 10110,011₂
Задание №2. Выполните сложение:

1) 100101₂+101₂ 7) 101101₂+111₂

2) 10111111₂[phone]₂ 8) 110010100₂[phone]₂

3) 1000000101,0101₂+1010000110,01₂ 9) 1000100001₂[phone]₂

4) 1101110011₂[phone]₂ 10) 1011011,01₂+1000101110,1001₂

5) 11110100₂[phone]₂ 11) 1101110₂[phone]₂

6) 1100110011,1₂+111000011,101₂ 12) 11001,1₂+11,01₂
Задание №3. Переведите числа из одной системы счисления в другую

1) 10001₂ - А ₁₀ 4) 10101₂ - А₁₀ 7) 89₁₀ - А ₂

2) 4567₈ - А₁₀ 5) 10011₂ - А₁₀ 8) 11101₂ - А₁₀

3) 512₁₀ - А ₂ 6) 4067₈ - А₁₀ 9) 312₁₀ - А ₂
Задание №4. Выполните умножение чисел.

1) 1001011₂*1010110₂; 3) 100001₂*10010₂ 5) 111101₂*1010111₂

2) 1001001₂*100010₂ 4) 1001000₂*1010011₂ 6) 11011,011₂*11001,001₂
Задание 5. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

1) 563 3) 264 5) 234,25 7) 53,125 9) 286,16

2) 737 4) 92 6) 934,25 8) 413,5625 10) 100,94

Задание №6. Переведите числа в десятичную систему счисления.

1) 1100010010₂ 7) 10011011₂ 13) 1111000001,01₂

2) 416,1₈ 8) 1100111001₂ 14) 1111011,001₂

3) 110000101,01₂ 9) 1601,56₈ 15) 16E,B4₁₆

4) 1000100₂ 10) 110000100,001₂ 16) 101011111,00011₂

5) 665,42₈ 11) 246,18₁₆ 17) 10110111,01₂

6) 1110000010₂ 12) 10011101₂
Задание №7. Укажите, какие числа записаны с ошибками. Ответ обоснуйте.

1) 156₇ 3) 3005,23₄ 5) 185,794₈ 7) 1102₂

2) 1345,52₆ 4) 112,011₃ 6) 16,545₅.
Дополнительные задания

Задание 1

Задание 1. Переведите из восьмеричной системы счисления в десятичную

250	2022	2757	123	247	2021	2756	122	246	2020
2755	121	244	2016	2753	117	243	2015	2752	116
242	2014	2751	115	241	2013	2750	114	240	2012
2747	113	237	2011	2746	112	236	2010	2745	111

Задание 2. Определите десятичный эквивалент шестнадцатеричных чисел

113	2ACF	691	D306F	112	2ACE	690	D306E	111	2ACD
68F	D306D	10F	2ACB	68D	D306B	10E	2ACA	68C	D306A
10D	2AC9	68B	D3069	10C	2AC8	68A	D3068	10B	2AC7
688	D3067	10A	2AC6	688	D3066	109	2AC5	687	D3065

Задание 3. Переведите координаты точек в 10-ую СС и постройте рисунок в координатной плоскости:

1. 
   ^{( 1; 11)}
   
2. 
   ^{(101; 11)}
   
3. 
   ^(101;1001)
   
4. 
   ^{(1000; 110)}
   
5. 
   ^{(101; 11)}
   
6. 
   ^{(1010; 110)}
   
7. 
   ^{(1001; 1)}
   
8. 
   ^(11;1)
   
9. 
   ^(1;11)
   
10. 
    ^{(101; 1001)}
    
11. 
    ^{(101; 1010)}
    
12. 
    ^{(1000; 1010)}
    
13. 
    ^{(1000; 1001)}
    
14. 
    ^{(101; 1001)}
    

По данным в 10-ой системе получите 16-ый эквивалент и заполните столбцы таблицы. Отметьте полученные точки, пронумеруйте их на графике и последовательно их соедините; соедините точки 1 и 19.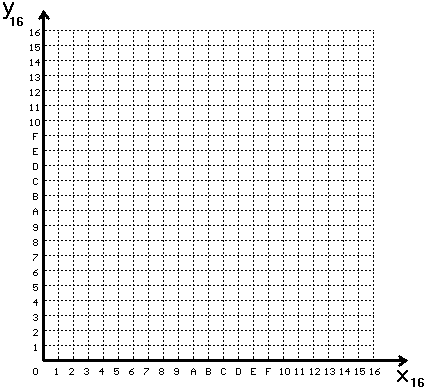

№	1	2	3	4	5	6	7	8	9	10	11	12
x10	16	14	14	9	14	10	14	11	14	12	15	18
y10	7	7	9	9	12	12	15	15	18	18	21	18

№	13	14	15	16	17	18	19
x10	16	19	16	20	16	21	16
y10	18	15	15	12	12	9	9

№	1	2	3	4	5	6	7	8	9	10	11	12
x16
y16

№	13	14	15	16	17	18	19
x16
y16

По данным в 10-ой системе получите 8-ый эквивалент и заполните соответствующие столбцы таблицы. Отметьте полученные точки, пронумеруйте их на графике и последовательно их соедините.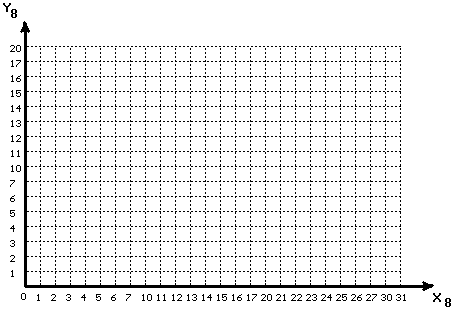

№	1	2	3	4	5	6	7	8	9
X10	2	4	5	10	10	5	7	20	11
Y10	6	6	5	5	6	6	16	6	6

№	10	11	12	13	14	15	16	17
X10	11	20	23	24	20	4	2	2
Y10	5	5	7	7	2	2	5	6

№	1	2	3	4	5	6	7	8	9
X8
Y8

№	10	11	12	13	14	15	16	17
X8
Y8

Ответьте на вопросы

1. 
   Как представлено число 83₁₀ в двоичной системе счисления?
   
2. 
   Сколько единиц в двоичной записи числа 195?
   
3. 
   Как представлено число 25 в двоичной системе счисления?
   
4. 
   Как представлено число 82 в двоичной системе счисления?
   
5. 
   Как представлено число 263 в восьмеричной системе счисления?
   
6. 
   Как записывается число 567₈ в двоичной системе счисления?
   
7. 
   Как записывается число A87₁₆ в восьмеричной системе счисления?
   
8. 
   Как записывается число 754₈ в шестнадцатеричной системе счисления?
   
9. 
   Сколько единиц в двоичной записи числа 173?
   
10. 
    Дано: , . Какое число С, записанное в двоичной системе счисления, удовлетворяет неравенству ?
    
11. 
    Дано: , ., Какое число С, записанное в двоичной системе счисления удовлетворяет неравенству ?
    
12. 
    Дано: , . Какое число С, записанное в двоичной системе счисления, удовлетворяет неравенству ?
    
13. 
    Дано: , . Какое число С, записанное в двоичной системе счисления, удовлетворяет неравенству ?
    
14. 
    Дано: , Какое число С, записанное в двоичной системе счисления , удовлетворяет неравенству ?
    
15. 
    Дано: , . Какое число С, записанное в двоичной системе счисления, удовлетворяет неравенству ?
    
16. 
    Дано: , . Какое число С, записанное в двоичной системе счисления, удовлетворяет неравенству ?
    
17. 
    Вычислите сумму чисел x и y, при x = A6₁₆, y = 75₈. Результат представьте в двоичной системе счисления.
    
18. 
    Значение выражения 10₁₆ + 10₈ • 10₂ в двоичной системе счисления равно
    
19. 
    Вычислите сумму двоичных чисел x и y, если x = 1010101₂ и y = 1010011₂
    
20. 
    Вычислите значение суммы 10₂ + 10₈ +10₁₆ в двоичной системе счисления.
    
21. 
    Вычислите сумму чисел x и y, при x = 271₈, y = 11110100₂. Результат представьте в шестнадцатеричной системе счисления.
    
22. 
    Вычислите сумму чисел x и y, при x = A1₁₆, y = 1101₂. Результат представьте в десятичной системе счисления.
    
23. 
    Вычислите сумму чисел x и y, при x = 56₈, y = 1101001₂. Результат представьте в двоичной системе счисления.
    
24. 
    Вычислите сумму чисел x и y, при x = 5A₁₆, y = 1010111₂. Результат представьте в восьмеричной системе счисления.
    
25. 
    Вычислите сумму чисел x и y, при x = 127₈, y = 10010111₂. Результат представьте в десятичной системе счисления.
    
26. 
    Вычислите A81₁₆ + 377₁₆. Результат представьте в той же системе счисления.
    

ЭТО ИНТЕРЕСНО

27. 
    Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам: а)[101101₂;110000₂]; б) [14₈; 20₈]; в) [28₁₆; 30₁₆].
    
28. 
    В классе 1111₂ девочек и 1100₂ мальчиков. Сколько учеников в классе?
    
29. 
    В классе 36_q учеников, из них 21_q девочек и 15_q мальчиков. В какой системе счисления велся счет учеников?
    
30. 
    В саду 100_q фруктовых деревьев, из них 33_q яблони, 22_q груши, 16_q слив и 5_q вишен. В какой системе счисления посчитаны деревья?
    
31. 
    У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?
    
32. 
    Некогда был пруд, в центре которого рос один лист водяной лилии. Каждый день число таких листьев удваивалось, и на десятый день вся поверхность пруда уже была заполнена листьями лилий. Сколько дней понадобилось, чтобы заполнить листьями половину пруда? Сколько листьев было после девятого дня?
    
33. 
    Путем подбора степеней числа 2, в сумме дающих заданное число, переведите в двоичную систему счисления следующие числа: а) 5; б) 7; в) 12; г) 25; д) 32; е) 33.
    

Список литературы
1. Семакина И.Г., Хеннер Е.К. Информатика. Задачник-практикум: Т.2 – М.: Бином. Лаборатория Знаний, 2002.-280с.

2. Угринович Н. Информатика и информационные технологии. Учебное пособие. - М.: БИНОМ. Лаборатория знаний, 2005.

3. Шауцукова Л. З. Информатика 10-11 кл. Учебное пособие. - М.: Просвещение, 2003.

4. Могилев А.В., Пак Н.И., Хеннер Е.К.. Информатика. Учебное пособие: 8 издание – М.: 2012, 848с.

5. Макарова Н.В., Волков В.Б. Информатика Питер, 2011, с.576