19 сценарий - Целая брошюра с расписанием и играми. Сказка по теме Решение уравнений
 Скачать 2.08 Mb. Скачать 2.08 Mb.
|
|
УРОК – ОБОБЩЕНИЕ ПО АЛГЕБРЕ 10 КЛАССА ПО ТЕМЕ «ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ» ЦЕЛЬ: Раскрытие возможностей простейших преобразований для построения сложных графиков. ХОД УРОКА. 1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ. Учитель: Сегодня мы с вами вспомним основные понятия по данной теме, знакомые вам из курса алгебры. Немного уточним их с точки зрения начал анализа. И вообще поговорим о значении данной темы в жизни человека. ПОВТОРЕНИЕ в форме фронтального опроса. Что называется графиком? (Ответ: это множество точек координатной плоскости, у которых значения х и у связаны некоторой зависимостью и каждому значению х соответствует единственное значение у). Где в жизни мы встречаемся с графическим способом представления информации и для чего? (Ответ: графический способ – один из самых удобных и наглядных способов представления и анализа информации. Например: метеорологическая служба фиксирует изменения температуры и может сравнить с показаниями в данный момент, но несколькими годами раньше. Используя показания сейсмографов фиксируются колебания почвы и предсказываются землетрясения и цунами. Врачи выявляют болезни сердца, изучая графики кардиограмм. Широко используются графики в экономике: кривые спроса и предложения, линии производственных возможностей и т.д.) Что называется функцией? (Ответ: функция – это зависимость величины у от величины х при которой каждому значению х поставлено в соответствие единственное значение у.) Что важно знать про функцию? (Ответ: область определения, область значений, поведение функции на отдельных промежутках) ПРЕОБРАЗОВАНИЕ ГРАФИКОВ. УЧИТЕЛЬ: если известен график некоторой функции у = F (х), то с помощью простейших преобразований (осевой и центральной симметрий, параллельного переноса ) можно построить графики более сложных функций. ЗАДАЧА №1: Построить графики функций у = х2 , у = х2 – 4 и у = х2 + 4 . РЕШЕНИЕ: Составим таблицу значений для этих функций на промежутке [-4; 4] с шагом 1. Построим графики функций в одной системе координат. Легко заметить, что значения второй функции в каждой точке на 4 меньше, чем первой. А значения третьей функции в каждой точке на 4 больше, чем первой. А графики этих функций получаются параллельным переносом.
ПРАВИЛО №1. График функции у = F (х) + к получается параллельным переносом графика у = F (х) в отрицательном направлении оси Оу на к единиц , если к <0 и в положительном направлении оси Оу на к единиц, если к > 0. Очевидно, что для построения таких графиков достаточно построить график функции у = F (х) и осуществить преобразования для нескольких точек. Чем больше точек кривой будет взято для преобразования, тем точнее получится график заданной функции. ЗАДАЧА №2: Построить графики функций у = х2 , у = 2х2 и у = (1/2)х2 . РЕШЕНИЕ: Составим таблицу значений для этих функций на промежутке [-3; 3] с шагом 1. Построим графики в одной системе координат. Легко заметить, что для каждого значения х значения у увеличиваются в 2 раза (кроме точки 0) для второй функции, то есть график как бы растягивается вдоль оси Оу, а значения третьей функции уменьшаются в 2 раза по отношению к значениям первой функции, то есть график как бы сжимается вдоль оси Оу.
ПРАВИЛО №2. График функции у =а F (х) получается растяжением графика у = F (х) вдоль оси Оу в а раз , если а > 1 и сжатием вдоль этой оси в 1/а раз при 0 <а <1. Задача №3: Построить графики функций у = х2 , у = (х -2)2, у = (х+2)2 РЕШЕНИЕ: Строим таблицу значений для данных функций на промежутке [-4; 4] с шагом 1. Построим графики в одной системе координат.
ПРАВИЛО №3. График функции у = F (х+с) получается параллельным переносом графика у = F (х) в отрицательном направлении оси Ох( на с единиц влево), если с > 0 и в положительном направлении оси Ох (на с единиц вправо) , если с <0. Задача №4: Построить графики функций у = х2 у = - х2 . РЕШЕНИЕ: Строим таблицу значений для данных функций на промежутке [-4; 4] с шагом 1. Построим графики в одной системе координат. Легко заметить, что для противоположных значений х значения у противоположны, поэтому графики будут симметричными относительно оси Ох.
ПРАВИЛО №4. График функции у = -F (х) получается симметричным отображением графика у = F (х) относительно оси абсцисс Ох. Задача №5: Построить графики функций у = х2 у = -2(х – 3)2 + 4 . РЕШЕНИЕ: Применяя полученные правила к решению данной задачи, анализируем данные и приходим к выводу: график функции у = -2(х – 3)2 + 4 получен из графика у = х2 следующим образом: 1) строим график у1 = х2 2) строим график у2 = 2х2 – растяжение вдоль оси Оу в 2 раза 3) строим график у3 = - 2х2 - симметрия относительно оси Ох 4) строим график у4 = - 2(х – 3)2 – сдвиг вправо вдоль оси Ох на 3 единицы 5) строим график у5 = - 2(х – 3)2 + 4 – сдвиг вверх вдоль оси Оу на 4 единицы 6) вершина параболы переместилась в точку (3; 4). 4. ПРОВЕРКА УСВОЕНИЯ МАТЕРИАЛА. ТЕСТ «ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ» ЦЕЛЬ: Проверка усвоения материала обучающимися. Вариант №1. Точка М (4;2) принадлежит графику функции у = F (х). Отметьте крестиком соответствующую ей точку на графике указанной функции.
Вариант №2. Точка М (-2;4) принадлежит графику функции у = F (х). Отметьте крестиком соответствующую ей точку на графике указанной функции.
Вариант №3. Точка М (2;4) принадлежит графику функции у = F (х). Отметьте крестиком соответствующую ей точку на графике указанной функции.
5. ИТОГ УРОКА. С помощью мультимедийной презентации обучающимся предлагается вспомнить об основных преобразованиях графиков функций. 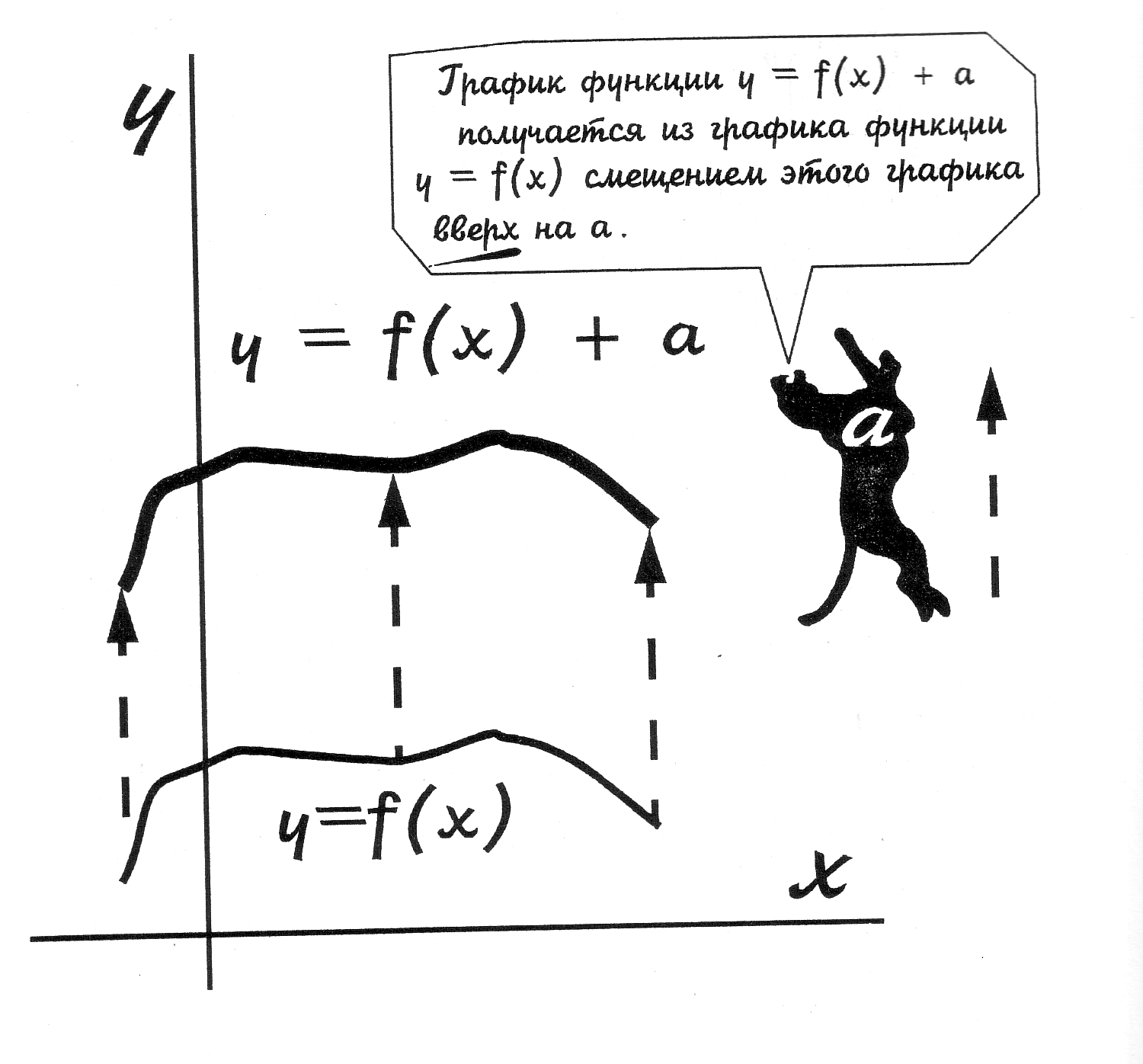 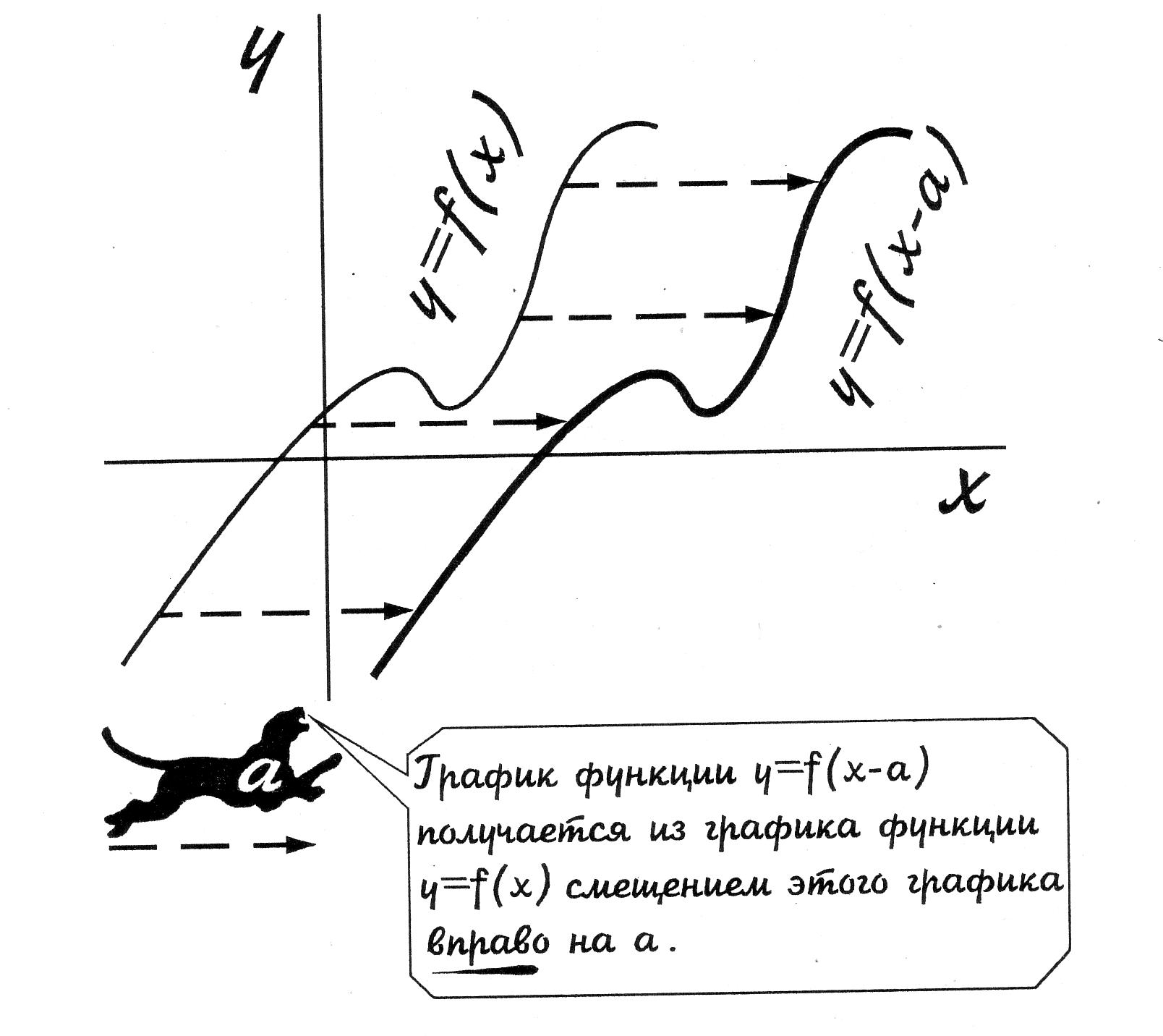 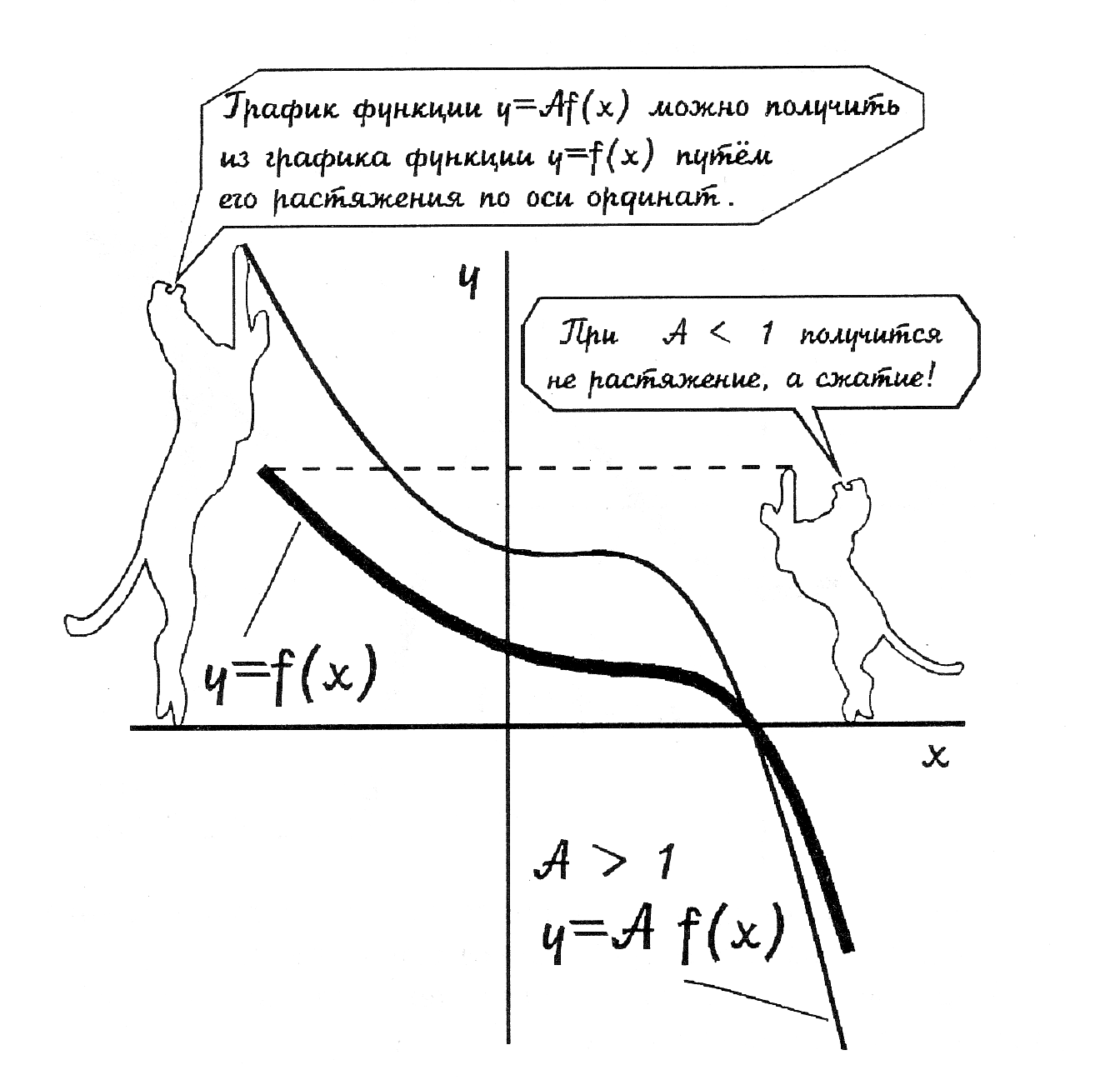 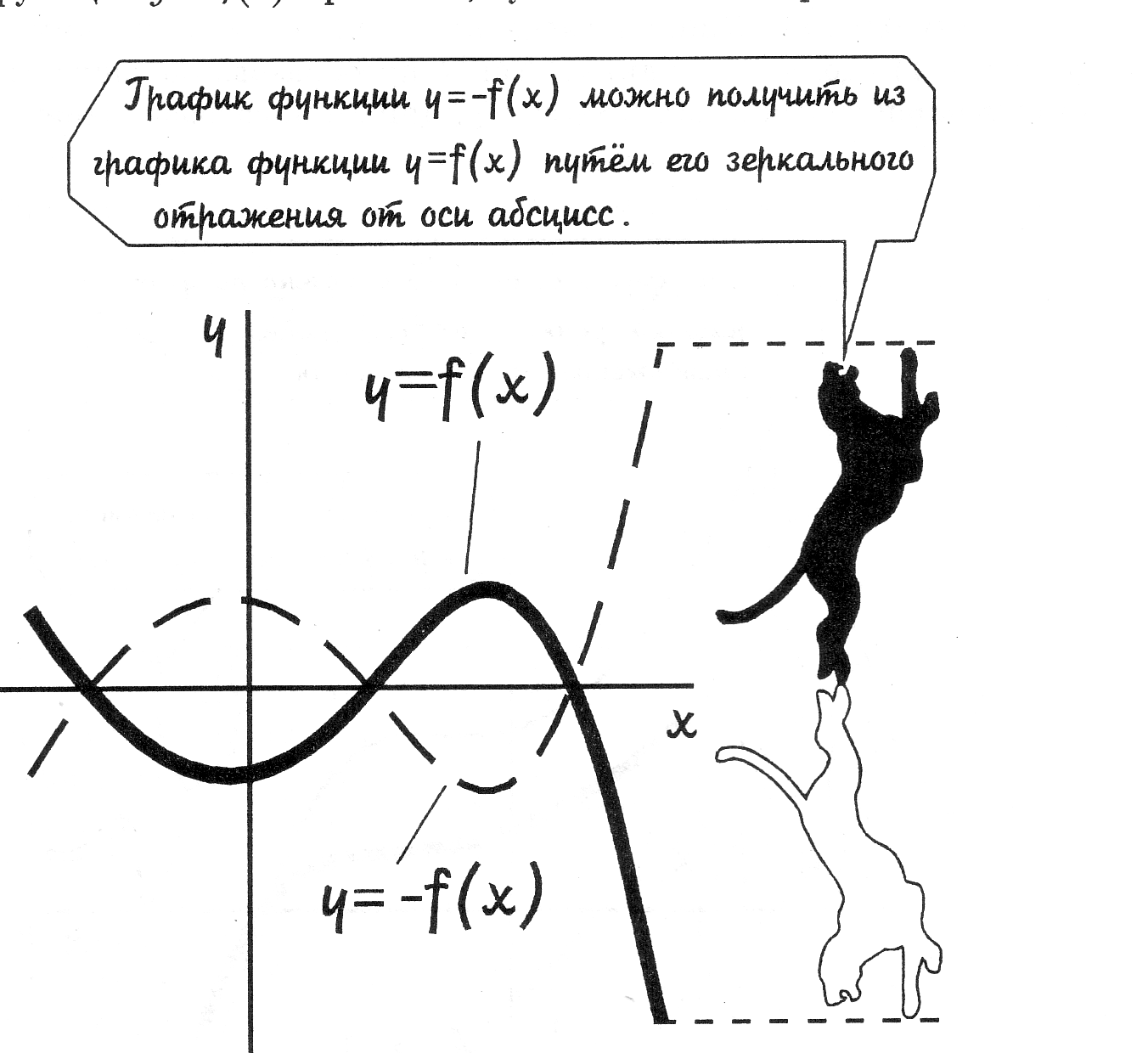 ЗАДАНИЕ НА ДОМ. Даётся по учебному пособию «Алгебра и начала анализа. Учебник для 10 – 11 класса общеобразовательных учреждений» под редакцией А.Н.Колмогорова : пункт 3, страница 21 – 28, № 48 (а; б), № 49 (а; б), № 50(а;б) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
