Следящая система

• Название: Следящая система
• Дата: 05.03.2023
• Размер: 146 Kb.
• Имя файла: TAU_kursach.docx
• Тип: Курсовой проект; #969470
• страница: 4 из 7

§4 Определение параметров линейной системы автоматического регулирования по наименьшей квадратичной оценке качества.

Если переходный процесс колебательный – то о нем можно судить по наименьшей квадратичной интегральной оценке качества.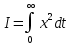



Параметры системы, обеспечивающие минимум интеграла – оптимальны. Пусть уравнение статической системы, где задающее воздействие постоянно будет иметь вид: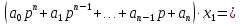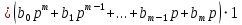





Отклонение регулируемой величины от ее нового установившегося значения в любой момент времени переходного процесса равно: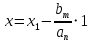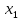



- текущее значение регулируемой величины, отсчитываемое от ее старого установившегося значения при единичном скачке.

При единичной оценке при этих условиях А.А. Красовский предложил формулу: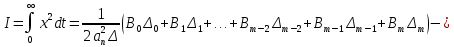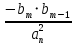





где – определитель Гурвица, составленный из коэффициентов: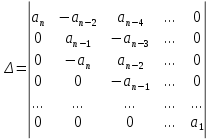



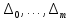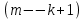Определители получают заменой столбца столбцом .

Коэффициенты определяют как:



Динамика системы описывается уравнением: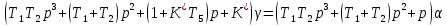



В общем виде: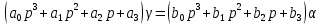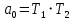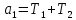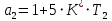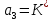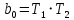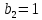

















Для вычисления интеграла применяем формулу: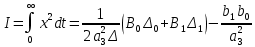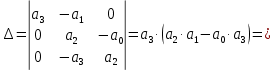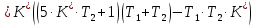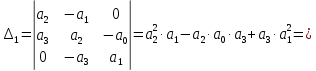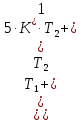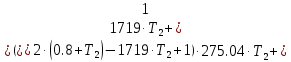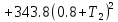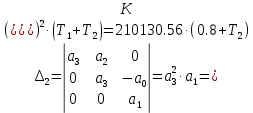



















Подставим в (1) для I, получим: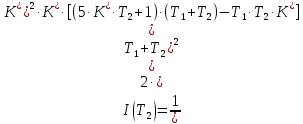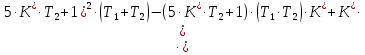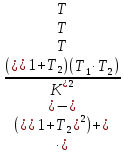







Подставив и , получим: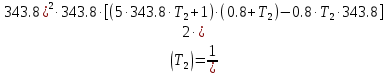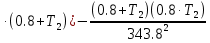









Построим график I(T₂) (рис. 7):

T2	0,02	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5
I(T2)	0,000046	0,003	0,014	0,038	0,081	0,147	0,241	0,368	0,533	0,740	0,996

Пример расчета при T_{2 =} 1: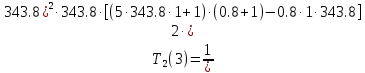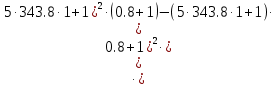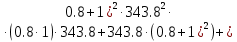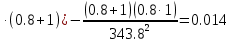









Минимальное значение 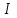будет при

В результате видно, что переходный процесс длится меньше по времени, чем переходный процесс в методе определения параметров по наибольшей степени устойчивости.