Следящая система
 Скачать 146 Kb. Скачать 146 Kb.
|
§2 Проверка системы на устойчивостьТ.к. следящая система описывается уравнением третьего порядка, то для ее исследования на устойчивость нужно пользоваться критерием Вышнеградского, по которому для устойчивости линейной системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительны и произведение средних коэффициентов было бы больше произведения крайних. Построение границы устойчивости. 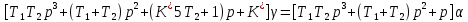 Общий вид: 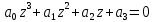 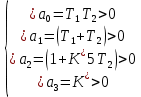  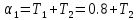 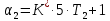 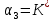 Система находится на границе устойчивости, если:  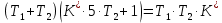 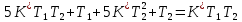 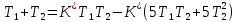 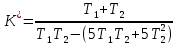 Построим график 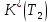 (рис. 3): (рис. 3):
Пример расчета при  : :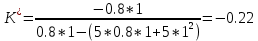 Если 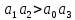 – система устойчива. – система устойчива.Если 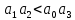 – система неустойчива. – система неустойчива.TРассмотрим А (2;-0.05) и B (3;-0.1) Для А: 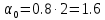 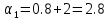 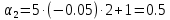 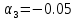 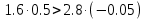 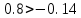 Система устойчива Для B: 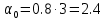 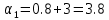 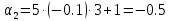  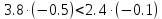  Система неустойчива §3 Определение параметров системы по наибольшей степени устойчивости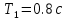 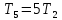 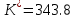 Нормальное уравнение: 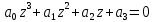 Смещенное уравнение: 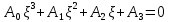 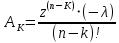 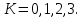 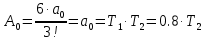 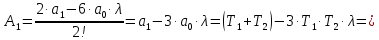 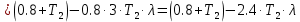 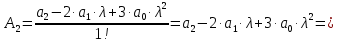 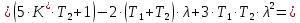 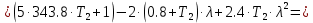  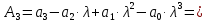 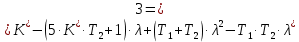  Смещенное уравнение 3-го порядка, поэтому воспользуемся критерием Вышнеградского, т.е. условием апериодической степени устойчивости, когда 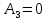 и условием колебательной степени устойчивости, когда и условием колебательной степени устойчивости, когда 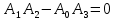 Для апериодической степени устойчивости:  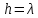 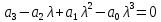 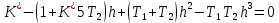 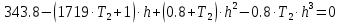 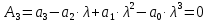 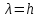 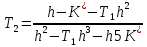 Пример расчета при 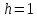 : :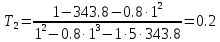 Построим график h(T2) (рис. 4)
Колебательная степень устойчивости: 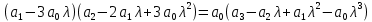 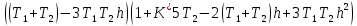 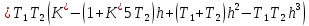 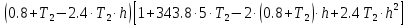 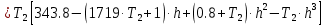 Пример расчёта при 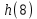 : :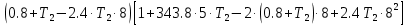 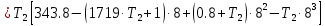 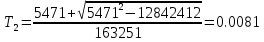 Построим график h(T21)(рис. 5)
|
