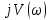Следящая система

1 2 3 4 5 6 7

§7 Проверка САУ на устойчивость по методу Михайлова.

Характеристический полином: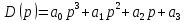

Вещественная функция Михайлова:

Мнимая функция Михайлова:

Годограф Михайлова: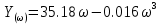

Пример расчета при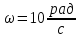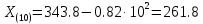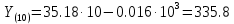

Построим годограф Михайлова (рис. 8):

Т.к. годограф Михайлова, при изменении

от 0 до ∞, начинаясь при

на вещественной положительной полуоси

, обходит против часовой стрелки последовательно три квадранта координатной плоскости, то САУ по критерию Михайлова является устойчивой.

Позволяет судить об устойчивости замкнутой системы по виду АФХ разомкнутой системы.

Передаточная функция разомкнутой цепи: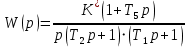

Будем считать, что b₃ = 1, тогда заменив p =

, частотная передаточная функция имеет вид: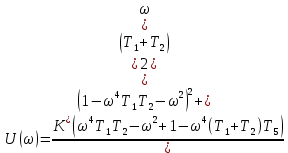

Пример расчета при

Построим годограф Найквиста (Рис. 9):

Так как годограф Найквиста, при изменении

от 0 до ∞ охватывает точку -1 на оси абсцисс - эта замкнутая система будет неустойчивой.

1 2 3 4 5 6 7