Валидность тестов. Словарьсправочник по психодиагностике издание 2е, переработанное и дополненное Серия Мастера психологии

• Название: Словарьсправочник по психодиагностике издание 2е, переработанное и дополненное Серия Мастера психологии
• Дата: 10.08.2022
• Размер: 5.87 Mb.
• Имя файла: Валидность тестов.doc
• Тип: Справочник; #643669
• страница: 23 из 71

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ —

комплекс методов статистического иссле­дования взаимозависимости между пере­менными, связанными корреляционными отношениями. Корреляционными (лат. correlatio — соотношение, связь, зависи­мость) считаются такие отношения меж­ду переменными, при которых выступает преимущественно нелинейная их зависи­мость, т. е. значению любой произвольно взятой переменной одного ряда может со­ответствовать некоторое количество зна­чений переменной другого ряда, откло­няющихся в ту или иную сторону от среднего.

К. а. выступает в качестве одного из вспомогательных методов решения теоре­тических задач психодиагностики и вклю­чает в себя комплекс наиболее широко применяемых статистических процедур при разработке тестовых и других психо­диагностических методик, определения их надежности, валидности. К. а. явля­ется одним из основных методов статис­тической обработки эмпирического мате­риала в прикладных психодиагностичес­ких исследованиях.

Существующие процедуры К. а. поз­воляют определить степень значимости связи, установить меру и направление влияния одного из признаков (X) на ре­зультирующий признак (У) при фиксиро­ванном значении отдельных переменных (корреляция частная), выявить степень и направленность связи результирующего признака (Y) с совокупностью перемен­ных jcj, х₂, -.- , x_k(корреляция множе­ственная). К. а. подлежат как количе­ственные, так и качественные признаки (к первым относятся переменные, измеряе­мые в интервальной шкале и шкале отно-

шений, ко вторым — не имеющие единиц измерения, оцениваемые шкалами наиме­нований и порядковыми шкалами) (см. Шкалы измерительные). Может быть ■также установлена корреляция и для при­знаков, один из которых является каче­ственным, а другие количественными (корреляция бисериальная, корреляция качественных признаков).

Одним из основных принципов опреде­ления количественных критериев корре­ляционной связи — коэффициентов кор­реляции — является сравнение величин отклонений от среднего значения по каж­дой группе в сопряженных парах сравни­ваемых рядов переменных. Другими сло­вами, определяется частота соответствия между шкалами Xи У. Предположим, один и тот же испытуемый получил высо­кие оценки по тесту вербальных способ­ностей (Х_{) и показателям успеваемости

по литературе (У^). Тогда произведения отклонений x,Jc и у{у принимают высо­кие положительные значения. Если же большому х₁у другого испытуемого будет соответствовать малое у^, то это произве­дение будет отрицательным. Абсолютная величина произведения отклонений зави­сит от степени отклонения переменных от среднего значения в сравниваемых парах. Если А" и У не имеют систематической связи (большие х сочетаются с малыми у и наоборот), различные произведения будут принимать положительные или отрицательные значения. Сумма произ­ведений во в£ех сравниваемых парах



будет приближаться к нулю. Сумма про­изведений в сравниваемых рядах перемен-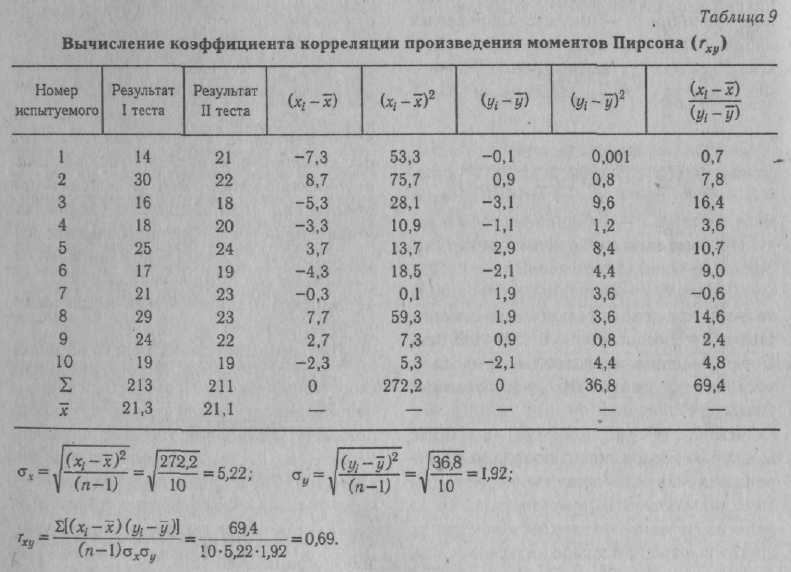



ных будет иметь большую величину по модулю и положительный знак, если Xи Yсвязаны между собой выраженной прямой зависимостью, и большую величи­ну и отрицательный знак при связи Xи Yсильной обратной зависимости.

С целью достижения независимости меры корреляционной связи от числа сравниваемых пар и величин стандартных отклонений в двух группах произведение отклонений делится на число сравни­ваемых пар и стандартные отклонения в сопоставимых рядах. Такая мера носит на­звание коэффициента корреляции — про­изведения моментов Пирсона: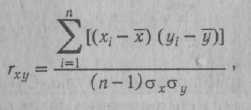



где Х[ и y_i— сравниваемые количествен­ные признаки, п — число сравниваемых наблюдений, а_хи а_у— стандартные от­клонения в сопоставимых рядах. Расчет­ная формула г_хуимеет следующий вид: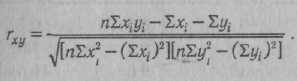



При вычислении коэффициента Пир­сона, особенно при большом количестве наблюдений, целесообразно упрощение за счет различных приемов, сокращаю­щих объем вычислений. В качестве при­мера приводим расчет результатов двух тестов в группе из 10 обследованных (табл. 9).

Определение статистической зависи­мости коэффициента г_хупроводится с по­мощью критерия Стьюдента (t):



где п' — число степеней свободы {п' = п -- 2). По таблице распределения Стью­дента для п'-8 находим £ = 2,896 при а ■ 0,02 и * = 2,306 при а = 0,05. Отсюда статистическая значимость установлен­ного значения корреляции признаков на уровне а > 0,02.

При возведении коэффициента корре­ляции Пирсона в квадрат получаем коэф­фициент детерминации г²_ху, выражаю­щий степень вариации переменных. В на­шем примере г²_ху - 0,48, что свидетель­ствует о том, что 48% измерений призна­ков объясняются их совместным распре­делением (взаимовлиянием),

КОРРЕЛЯЦИЯ БИСЕРИАЛЬНАЯ

(лат. bis series — два ряда, две серии) — метод корреляционного анализа отноше­ния переменных, одна из которых измере­на в дихотомической шкале наименова­ний, а другая — в интервальной шкале отношений или порядковой шкале. Назва­ние метода связано с тем, что сравнивают­ся две альтернативные серии объектов X, имеющие условные значения 0 или 1 по Y.

Наиболее характерно применение ко­эффициентов К. б. в психологической диагностике при анализе дискримина-тивности заданий теста, а также при определении валидности критериаль­ной путем коррелирования значений тес­товых оценок с независимыми характе­ристиками критерия, выраженными в ди­хотомической шкале (см. Шкалы изме­рительные).

Для описания связи между перечис­ленными видами переменных исполь­зуется точечный бисериальный коэффи­циент корреляции Пирсона: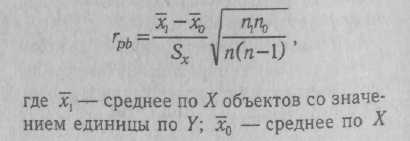



объектов со значением нуль по У; S_x— стандартное отклонение всех значений по X; rtj — число объектов, с единицей по У: щ — число объектов с нулем по У, т. е. п = П[ + п₀. Уравнение для вычисления г_рЬпредставляет собой алгебраическое упрощение формулы коэффициента г_ху (см. Корреляционный анализ) для слу­чая, когда У— дихотомическая перемен­ная. Можно привести ряд других эквива­лентных выражений, удобных для прак­тического применения: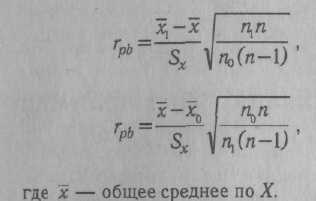



Значение г_рЬварьирует от -1 до +1. В том случае, когда переменные с единицей по Yимеют среднее по X, равное средне­му переменных с нулем по У, г_рЬобраща­ется в нуль.

В качестве примера можно привести вычисление г _ьпри анализе дискримина-тивностн отдельных пунктов опросника личностного, т. е. корреляции между ти­пичным ответом на отдельный пункт (ут­верждение—отрицание) с общим резуль­татом по тесту (табл. 10).

Вычисленное таким образом значение г_рЬпоказывает, что проверяемый пункт опросника имеет среднюю диагностичес­кую значимость и слабо коррелирует с об­щим результатом теста.

Достоверность (а) связи, рассчитан­ной с помощью коэффициента г_рЬ, может определяться с помощью критерия Я² для числа степеней свободы df = 2.

Другим распространенным методом расчета является определение бисериаль-ного коэффициента корреляции (г_ш), ко­торый применяется в тех случаях, когда

есть основания полагать, что дихотоми­ческое распределение близко к нормаль­ному:



Элементы уравнения идентичны ис­пользуемым при вычислении г_рЬ, за исключением величины U— ординаты

Таблица 10

Вычисление точечного бисериального ко­эффициента корреляции Пирсона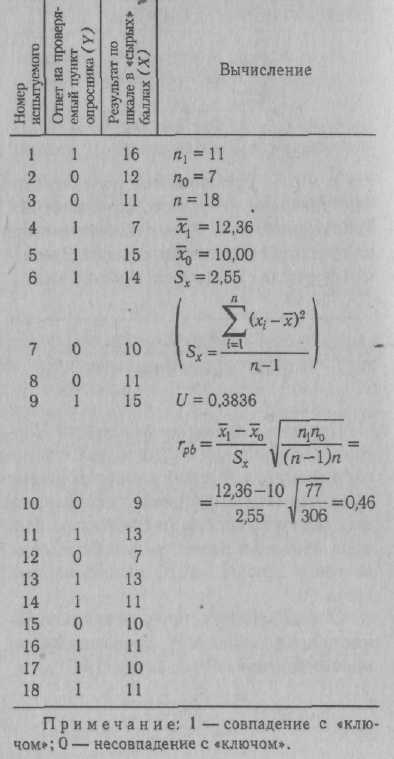







КОРРЕЛЯЦИЯ КАЧЕСТВЕННЫХ ПРИЗНАКОВ — метод анализа связи переменных, измеряемых в порядковых шкалах и шкалах наименований (см. Шкалы измерительные). Наиболее час-го такой корреляционный анализ прово­дят с помощью коэффициентов корреля­ции ранговой, используемых в случаях, когда обе переменные измеряются ег шка­лах порядка или легко могут быть преоб­разованы в ранги. При измерении сравни­ваемых переменных в шкалах наименова­ний широко применяются коэффициенты сопряженности, в которых в качестве про­межуточной расчетной величины исполь­зуется критерий согласия Пирсона (см. Критерий X²). Наиболее часто в таких расчетах пользуются коэффициентом со­пряженности Пирсона: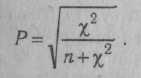



Значение Р всегда положительно и из­меряется от нуля до единицы. Особеннос­тью коэффициента сопряженности Пир­сона является то, что максимальное его значение всегда меньше +1 и в значитель­ной степени зависит от количества на­блюдений (размера таблицы). В случае квадратной таблицы (k x k)





где t— число столбцов таблицы, k— чис­ло строк таблицы.

В психологической диагностике опи­санные коэффициенты используются от­носительно редко.

КОРРЕЛЯЦИЯ РАНГОВАЯ — метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Наиболее часто К. р. применяется для анализа свя­зи между признаками, измеряемыми в по­рядковых шкалах (см. Шкалы измери­тельные), а также как один из методов определения корреляции качественных признаков. Достоинством коэффициен­тов К. р. является возможность их ис­пользования независимо от характера распределения коррелирующих призна­ков.

В практике наиболее часто применя­ются такие ранговые меры связи, как ко­эффициенты К. р. Спирмена и Кендалла. Первым этапом расчета коэффициентов К. р. является ранжирование рядов пере­менных. Процедура ранжирования начи­нается с расположения переменных по возрастанию их значений. Разным значе­ниям присваиваются ранги, обозначае­мые натуральными числами. Если встре­чаются несколько равных по значению пе­ременных, им присваивается усреднен­ный ранг (табл. 12).

В табл. 13 приведены данные для рас­чета коэффициентов К. р. Во второй гра­фе представлены ранжированные пока­затели по первому из сравниваемых рас­пределений (оценка IQ, в третьей гра­фе — соответствующие им данные теста зрительной памяти-).

Коэффициент корреляции рангов Спирмена (r_s) определяется из уравне­ния: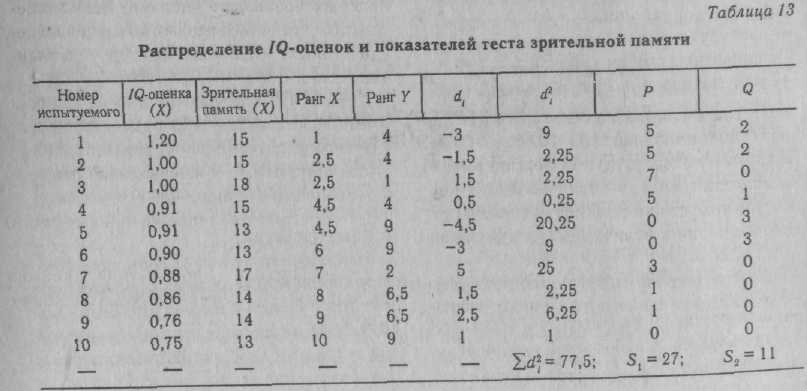









ент х более информативен, чем r_s, и рас­считывается проще. Поэтому на практике при расчете К. р. отдают предпочтение ко­эффициенту т.

КОСА КУБИКИ — невербальный тест интеллекта. Предложен К. Косом в 1920 г.

Испытуемому предлагают составить фигуры из цветных кубиков по рисункам-образцам. Тестовый материал состоит из шестнадцати кубиков с ребром 2,5 см, сто­роны которых окрашены в красный, бе­лый, желтый и синий цвета. Оставшиеся две противоположные грани разделены по диагонали, причем одна окрашена в белый и красный цвета, а вторая — в синий и желтый (см. Векслера интеллекта из­мерения шкалы, рис. 13). В набор вклю­чены восемнадцать образцов фигур, пер­вый из которых является тренировочным и выполняется совместно с испытуемым. Цвета рисунков-образцов соответствуют цветам кубиков, но размеры образцов вдвое меньше. Образцы размещены посе­редине картонной карточки, имеющей размер 10 х 7,5 см.

Задания следуют в порядке возраста­ющей трудности, что обеспечивается пос­ледовательной комбинацией следующих условий:

— фигуру можно построить только из од­ноцветных сторон кубиков;

— для построения фигуры следует ис­пользовать несколько двухцветных граней;

— фигуру можно сложить только из двухцветных сторон или из сочетания двухцветных и одноцветных, причем на образце не обозначена граница между соседними кубиками;

— образец повернут на 45°, т. е. стоит на ребре;

— для составления фигур требуется ис­пользовать все большее количество кубиков;

— образцы постепенно становятся все менее симметричными;

— увеличивается количество цветов на образце;

— образец не ограничивается рамкой, так что на краях сливается с фоном. Образцы-рисунки испытуемому предъ­являются последовательно,тестирование прекращается после пяти последовавших друг за другом неудачных решений. Ус­пешность оценивается с нескольких пози­ций. Самым важным показателем явля­ется время решения отдельных заданий. В протоколе фиксируется и количество попыток при выполнении. Первичные оценки по результатам выполнения зада­ний переводятся в показатель умствен­ного возраста. В более поздних модифи­кациях оценки переводятся в IQ-показа-тели стандартные. Данные дополняют­ся качественным анализом поведения ис­пытуемого.

К. к. принадлежат к часто применяе­мым тестам и широко используются как в оригинальной, так и в сокращенных моди­фикациях (см., напр., Векслера интел­лекта измерения шкалы). Ценность те­ста определяется особенностями деятель­ности испытуемого, которая моделирует- -ся его заданиями. Испытуемый начинает выполнение задания с анализа образца, путем сопоставления фрагментов образца с гранями кубиков. Затем осуществляет­ся генерализация выделяемого признака. Вслед за этим осуществляется переход к синтезу—констатация соответствия между образцом и собранной из кубиков фигурой. По мнению К. Коса, в ходе реше­ния заданий задействуются все мысли­тельные процессы.

Имеются сведения о валидности кон-структной К. к. Получена значимая кор­реляция с Вине—Симона умственного развития шкалой (г = 0,82 у нормаль­ных детей и г = 0,67 у слабоумных детей). Изучались связи показателей К. к. с

основными тестами интеллекта, в частно­сти Станфорд—Бине умственного раз­вития шкалой (г = 0,77), Равена про­грессивными матрицами (г = 0,81). Об­ращается внимание на независимость друг от друга показателей К. к. и тестов арифметических способностей.

Наиболее широкое применение К. к. находят в клинической психодиагностике (В. М. Блейхер, И. В. Крук, 1986). По данным Л. Кошча (1976), тест весьма по­лезен при работе с такими разнообразны­ми контингентами испытуемых, как твор­ческие личности с высоким уровнем спо­собностей и, с другой стороны, умствен­но отсталые лица; дети с минимальной мозговой дисфункцией, нарушением кон­центрации внимания, нарушением про­странственной ориентировки; дети, стра­дающие неврозами; дети с задержкой психического развития, педагогически за­пущенные; больные юношеского и зрело­го возраста, страдающие шизофренией. Тест может использоваться и при анали­зе интеллектуального потенциала здоро­вых лиц.

В отечественной психодиагностике К. к. используются чаще всего в том виде, как они представлены в соответствующем отдельно взятом субтесте Векслера ин­теллекта измерения шкалы.

КОЭФФИЦИЕНТ АЛЬФА (а) — ста

тистический показатель, используемый при дисперсионном анализе. Предложен Л. Кронбахом (1971). Наиболее часто при­меняется при оценке надежности теста. Уравнение К. А. имеет следующий вид: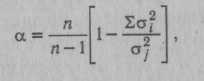



дартных отклонений для отдельных зада­ний. В том случае, если в методике при­меняются задания дихотомического типа («да»—«нет», «правильно»—«неправиль­но»), может быть использована упрощен­ная формула:

где п — количество заданий теста, а;² — квадрат стандартного отклонения для все­го теста, Zct,-² — сумма квадратов стан-



где SPQ = Xcy и Р — доля испытуемых, давших «ключевой» или правильный от­вет, а Q = 1 - Р. Дихотомический вариант К. А. является уравнением Кьюдера—Ри­чардсона (см. Надежность частей тес­та). Применение К. А. основано на моде­ли, предполагающей наличие большой дисперсии (а стало быть, и дискримина-тивности заданий теста) скорее у надеж­ного, чем у ненадежного теста (см. На­дежность факторно-дисперсионная). Таким образом, если при факторном анализе возвести в квадрат и просумми­ровать нагрузки выявленных факторов, можно определить надежность, поскольку нагрузки факторов представляют корре­ляцию теста с общими или специфически­ми факторами. Модель надежности фак­торно-дисперсионной близка к анализу надежности по внутренней согласо­ванности.

Факторно-дисперсионный метод ана­лиза надежности находится в сильной за­висимости от выбора переменных, в свя­зи с которыми факторизуется тест. Так, если сопоставлять тест математических способностей с личностными или мотива-ционными переменными, то оценка на­дежности была бы неадекватной (практи­чески не было бы общих факторов). С дру­гой стороны, если бы тест факторизиро-вался совместно с тестами общих способ­ностей так, чтобы каждый тест мог нагру­жать соответствующие ему факторы, ме­тод надежности факторно-дисперсионной

мог бы быть достаточно точным. Таким об­разом, эта модель подходит для оценки на­дежности теста, факторная валидность которого известна или задана прн разра­ботке, а также тестов, связанных с огра­ниченным числом общих факторов.