|
|
Валидность тестов. Словарьсправочник по психодиагностике издание 2е, переработанное и дополненное Серия Мастера психологии
НАДЕЖНОСТЬ ПАРАЛЛЕЛЬНЫХ ФОРМ — характеристика надежности психодиагностической методики с помощью взаимозаменяемых форм теста (см. Параллельная форма теста). При этом
одни и те же испытуемые в выборке определения надежности обследуются вначале с использованием основного набора заданий, а затем — с применением аналогичных дополнительных наборов. Коэффициент надежности по типу Н. п. ф. может быть определен и другим способом, а именно: испытуемые делятся примерно на равные группы, затем одной из них предлагается форма А теста, а другой — форма Б. Через определенное время (обычно не более недели) проводится повторное тестирование, но в обратном порядке.
Такая процедура обследования лишена значительной части недостатков способа определения надежности ретесто-вой. Так как в параллельной форме используется другой по содержанию материал, возможность тренировки и запоминания отдельных решений уменьшается. Важнейшим преимуществом данного метода является сокращение временного интервала перед повторным обследованием. Основным показателем Н. п. ф. является коэффициент корреляции между результатами первичного и повторного обследований, который позволяет оценить как временную стабильность теста (собственно надежность), так и степень соответствия результатов обеих форм теста. Если формы применяются непосредственно одна за другой, то корреляция отражает их взаимозаменяемость.
Отношение между параллельными формами теста имеет сложный характер. Оба набора заданий должны не только отвечать одним и тем же требованиям, измеряя идентичные показатели и давая сходные результаты, но вместе с тем быть относительно независимыми друг от друга. На практике эта задача осуществима далеко не для всех тестовых заданий (в особенности это касается личностных методик, опросников), что существенно ограничивает сферу применения Н. п. ф. Дру-
гим недостатком характеристики надежности по типу Н. п. ф. является возможность усвоения испытуемым принципа решения, общего для основной и параллельной форм. Таким образом, в случае оценки Н. п. ф. влияние тренировки и навыка, приобретаемого при повторном обследовании, если и снижается по сравнению с характеристикой надежности ретестовой, однако не устраняется полностью.
НАДЕЖНОСТЬ ПО ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ — способ определения надежности, опирающийся на оценку степени выраженности интеркорреляционных связей между заданиями, составляющими тест.
В данном случае истинный показатель по тесту понимается как результат, который получил бы испытуемый, если бы ему были предъявлены все возможные задания, относящиеся к черте или свойству, являющемуся объектом тестирования. Каждый конкретный тест является выборкой из генеральной совокупности заданий. Погрешность измерения отражает степень, в которой реальная выборка заданий охватывает теста заданий совокупность генеральную. Генеральная совокупность заданий порождает бесконечно большую корреляционную матрицу парных связей между заданиями. Среднее значение корреляции между заданиями для этой матрицы (Тц) указывает на степень общности, внутренней согласованности, заданий. Так, если, например, в тесте было бы одно задание из множества независящих друг от друга, то ?ц
0,00. Предполагается, что все задания имеют одинаковые значения взаимной корреляции.
Исходя из основных положений оценки Н. п. в. с, можно сказать, что корреляция некоторого задания с истинным показателем (г.() равна квадратному корню от
его средней корреляции с другими заданиями (Дж. Наннелли, 1978):
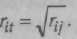
строго говоря, этот вывод справедлив тогда, когда количество заданий приближается к бесконечности.
С точки зрения разработчика теста, соотношение r.tи г.. имеет важное значение, поскольку при разработке значительного количества заданий и выборе из них тех, для которых значение лГц будет наибольшим, созданный тест будет надежным и свободным от погрешностей измерения. Аналогичные рассуждения, касающиеся взаимосвязи заданий, могут быть применены к надежности параллельных форм тестов. В данном случае каждый из параллельных тестов рассматривается как случайная выборка из генеральной совокупности заданий. Средние значения и дисперсии тестов отличаются от истинного показателя только случайным образом. Следовательно, в приведенном выше уравнении значения для заданий могут быть заменены показателями для тестов (т. е. наборов заданий).
Так как корреляции между заданиями или параллельными тестами на практике не являются идентичными, должно быть некоторое распределение их вокруг истинного значения. Если предположить, что такое распределение является нормальным (см. Нормальное распределение), можно оценить точность коэффициента надежности Тц путем вычисления стандартной ошибки (см. Ошибка измерения) средней взаимной корреляции заданий или тестов в генеральной совокупности (Дж. Наннелли, 1978):
ций задании внутри теста ил — количество заданий в тесте.
Из уравнения видно, что по мере возрастания стг. возрастают различия между корреляциями и по мере возрастания п стандартная погрешность уменьшается, то есть чем больше заданий, тем выше точность оценки коэффициента надежности. Действительно, если предположить, что сгг для некоторого теста равна 0,15, а количество заданий варьирует от 10 до 30, то, подставив соответствующие значения в уравнение, получим следующие погрешности: для теста из 10 заданий — 0,02; для теста из 20 заданий — 0,01; для теста из 30 заданий — 0,007.
Вслед за Дж. Наннелли (1978), П. Клайн (1986) распространяет суждение о возрастании точности коэффициента надежности при увеличении состава теста и на саму величину надежности. В самом деле, поскольку истинные показатели теста определяются через меру представленности заданий генеральной совокупности, должно выполняться предположение о том, что чем больше тест, тем выше корреляция с истинным показателем. Предельным случаем будет гипотетическая ситуация, когда тест состоит из всех заданий генеральной совокупности за исключением одного. Для доказательства надежности теста, задания которого, как заранее известно, принадлежат одной генеральной совокупности, можно воспользоваться формулой Спирмена— Брауна:
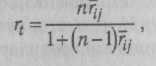
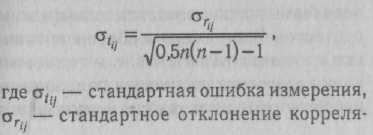
где rt— надежность теста, п —- количество заданий, Ц, — средняя взаимная корреляция заданий. В формуле Спирмена Брауна показатель г,' (см. Надежность частей теста) заменен на Тц , что вытекает из вывода модели коэффициента надежности.
Предположим, имеются три набора заданий (п = 10, 20, 30), средняя корреляция между которыми равна 0,20, тогда:
10-0.20 nRfi7 О667

Причем эти показатели получены для заданий, взаимная корреляция которых была низкой. Для более однородного теста из 30 заданий при 7ц = 40 получаем:

Таким образом, при наличии набора однородных заданий тест будет заведомо надежным. Даже если разделить совокупность заданий на две параллельные формы по 15 пунктов, они обе также будут иметь удовлетворительную надежность.
Теоретические значения коэффициента надежности при данном способе определения существенно превышают эмпирические значения надежности ретесто-вой и надежности параллельных форм. Это происходит из-за ряда допущений. Прежде всего следует указать на то, что при определении Н. п. в. с. не учитываются другие источники погрешности измерений, связанные с неконтролируемыми факторами среды, состояния и мотивации испытуемого (см. Надежность). В этой связи между Н. п. в. с. и ретестовой надежностью имеется противоречие. Ретес-товая надежность может уменьшаться при увеличении состава заданий (чем больше заданий, тем выше вероятность случайного или закономерного изменения ответа при ретесте). Противоречие может быть снято за счет признания некорректности допущения о равенстве интеркорре-
ляций между заданиями, зависимости погрешности лишь от представленности в тесте генеральной совокупности заданий. В противном случае необходимо было бы согласиться с тем, что в двух тестах, связанных общим фактором и имеющих одинаковое количество заданий, но совершенно разных по характеру выполнения и трудности, надежность будет одинаковой, что невозможно.
Следует обратить внимание на невозможность определения таким способом надежности тестов скорости, так как связь каждого из заданий исследуемой генеральной совокупности не определена из-за большого количества заданий, интеркорреляции заданий могут терять смысл (см., напр., Корректурная проба).
Важным аспектом оценки применимости Н. п. в. с. является парадокс, возникающий в этом случае при сочетании показателей надежности и валидности теста. Кажется, что высокая внутренняя согласованность должна быть основной целью разработчиков теста (Л. Кронбах, 1920). Такая точка зрения является довольно распространенной. Однако Р. Кэт-телл (1977) обоснованно утверждает, что высокая внутренняя согласованность (особенно при изучении сложных психологических конструктов, личностных показателей) в известном смысле противостоит высокой валидности.
Возникающее противоречие можно иллюстрировать следующим примером. Тест вербальных способностей может включать задания (и соответственно, субтесты) на подбор антонимов, синонимов, понимание слов, словарный запас. Предположим, что каждый из субтестов имеет высокие показатели Н. п. в. с. Однако если бы мы воспользовались только одним субтестом (например, подбором антонимов), то показатель Н. п. в. с. теста несомненно возрос бы по сравнению с полным набором субтестов, так как используется
только один тип высокосогласованных заданий. Высокая надежность субтеста антонимов будет отражать тот факт, что эта выборка заданий в высокой степени коррелирует с гипотетической генеральной совокупностью заданий на антонимы. Однако этот истинный показатель отражает не вербальные способности, а только способность подбирать антонимы (т. е. валид-ность теста станет низкой по отношению к измерению вербальных способностей). Приведенные данные свидетельствуют о специфичности применения каждого из имеющихся подходов к характеристике надежности теста. Н. п. в. с. имеет, очевидно, в основном теоретическое значение. Как и надежность частей теста в предельном случае разбивания материала на отдельные задания, рассматриваемый способ имеет практическое значение для оценки точности коэффициента надежности, а также при характеристике некоторых тестов, состоящих из специально подобранных факторизованных заданий (см. Факторно-аналитический принцип).
НАДЕЖНОСТЬ РЕТЕСТОВАЯ — характеристика надежности психодиагностической методики, получаемая путем повторного обследования испытуемых с помощью одного и того же теста. Надежность в этом случае вычисляется по соответствию результатов первого и второго обследований или по сохранению ранговых мест испытуемых в выборке при ретесте. Коэффициент надежности (г) соответствует коэффициенту корреляции между результатами таких обследований. При использовании интервальных шкал (см. Шкалы измерительные) применяется коэффициент корреляции произведения моментов Пирсона (см. Корреляционный анализ). Для шкал порядка в качестве меры устойчивости к перетестированию может быть использован коэффи-
циент ранговой корреляции Спирмена или Кэндалла (см. Корреляция ранговая).
При характеристике Н. р. особое значение имеет временнбй интервал между первым и вторым обследованиями. С его увеличением показатели корреляции имеют тенденцию к снижению, существенно повышается вероятность воздействия посторонних факторов — могут наступить закономерные возрастные изменения измеряемых тестом свойств, произойти различные события, влияющие на состояние и особенности развития исследуемых качеств. По этой причине при определении Н. р. стараются выбирать непродолжительные временные интервалы (до нескольких месяцев), а при обследовании детей младшего возраста эти интервалы должны быть еще меньше, поскольку возрастные изменения и развитие в этом случае происходят еще быстрее.
Несмотря на указанную тенденцию, при получении характеристик теста проводятся повторные испытания и с длительным временным промежутком. Иногда они осуществляются в целях оценки валидности прогностической, элементов валидности конструктной, связанных с дифференциацией по возрастному критерию и др. Определение же Н. р. главным образом ограничивается анализом краткосрочных случайных изменений, характеризующих тест как измерительную процедуру, а не его отношение к исследуемой области поведения.
Наряду с очевидной простотой Н. р. как метод определения надежности обладает существенными недостатками. Так, при повторном применении одних и тех же заданий, особенно при относительно непродолжительном временном интервале между обследованиями, у испытуемых может сформироваться навык работы с данной психодиагностической методикой, что приводит к улучшению индивидуальных результатов, хотя и не одинаково вы-
раженному у разных лиц. Это неизбежно ведет к заметной перестановке ранговых мест отдельных испытуемых в данной выборке и, соответственно, ухудшению коэффициента надежности. Еще более заметное воздействие на результаты анализа надежности оказывает запоминание испытуемыми отдельных решений, воспроизведение в повторном обследовании предыдущей картины правильных и неправильных решений. В этом случае результаты двух предъявлений теста не будут независимыми и корреляция между ними окажется завышенной.
Один из путей устранения влияния тренировки на результаты оценки Н. р. — формирование устойчивого навыка в работе с соответствующей методикой перед проведением тест-ретеста. Однако количество повторений теста при этом неизбежно возрастает, что приводит к увеличению числа запомнившихся решений. Такой прием может быть рекомендован для методик типа тестов скорости, содержащих большое количество элементов тестового материала.
Для других методик, очевидно, единственным приемлемым путем снижения влияния тренировки остается увеличение интервала ретеста, что, однако, как уже говорилось выше, вступает в противоречие с определением надежности как характеристики теста.
Для большинства тестов общих способностей характерно улучшение показателей Н. р. с возрастом испытуемых за счет лучшего контроля условий их выполнения. Другим фактором увеличения расчетных показателей Н. р. является относительное замедление с возрастом темпа психического развития в области тех характеристик, которые могут стать объектом измерения или влиять на результат теста. Благодаря этому, спустя время, составляющее интервал ретеста, случайные колебания результатов обследования ста-
новятся менее выраженными. Это искусственно завышает показатели Н. р. Эта закономерность требует отдельных измерений Н. р. в разных возрастных контин-гентах испытуемых, что особенно существенно для методик, предназначенных для обследования в широком возрастном диапазоне (см. Станфорд—Бине умственного развития шкала, Векслера интеллекта измерения шкалы).
Указанные особенности и недостатки метода определения надежности путем ретеста делают его пригодным лишь для ограниченного числа методик, допускающих многократное повторное обследование. К их числу относятся сенсомоторные пробы, тесты скорости и ряд других методик, отличающихся большим количеством пунктов (см. Миннесотский многоаспектный личностный опросник).
НАДЕЖНОСТЬ ФАКТОРНО-ДИСПЕРСИОННАЯ — способ определения
надежности, основанный'на дисперсионном анализе результатов теста. Надежность теста соответствует отношению истинной дисперсии (т. е. дисперсии самого исследуемого фактора) к реально полученной эмпирической дисперсии. По-_ следняя складывается из истинной дисперсии и дисперсии погрешности измерения (см. Ошибка измерения). Факторно-аналитический подход к определению надежности дополнительно расчленяет и дисперсию истинного показателя (Дж. Гилфорд, 1956).
Дисперсия истинного показателя, в свою очередь, может состоять из дисперсии общего фактора для групп аналогичных тестов (см. Фактор G), особых факторов, обеспечивающих тесты специфической направленности (см. Факторы групповые) и дисперсии факторов, присущих конкретной тестовой методике. Следовательно, полная дисперсия теста равна сумме дисперсий для общих, специфи-
ческих и единичных факторов плюс дисперсия погрешности:

2
где ах— доля дисперсии, выраженная общим фактором а, и т. д.
Таким образом, коэффициент надежности теста равен:
Факторно-дисперсионный способ определения надежности подходит для оценки уже факторизованного теста (см. Факторно-аналитический принцип), но не для тестов, измеряющих широкий набор разнообразных параметров, так как некоторые из них могут не входить в установленную область валидности методики.
НАДЕЖНОСТЬ ЧАСТЕЙ ТЕСТА —
характеристика надежности психодиагностической методики, получаемая путем анализа устойчивости результатов отдельных совокупностей тестовых задач или единичных пунктов (заданий) теста. Наиболее простым и распространенным способом определения Н. ч. т. является метод расщепления, суть которого заключается в выполнении испытуемым заданий двух равноценных частей теста. Обоснованием метода является вывод о том, что при нормальном или близком к нормальному распределении оценок по полному тесту (см. Нормальное распределение) выполнение любого случайного
набора из частей теста даст аналогичное распределение (при условии, что части однородны по характеру заданий по отношению к тесту в целом).
Для оценки надежности методом расщепления выбирают две эквивалентные по характеру и степени трудности группы задач (см. Внутренняя согласованность, Трудность заданий теста). Разделение объема заданий теста на сопоставимые части достигается:
— распределением заданий на четные и нечетные (в том случае, если задания в тесте строго ранжированы по степени субъективной трудности);
— распределением пунктов по принципу близости или равенства значений индексов трудности и дискриминативно-сти (см. Дискриминативность заданий теста). Такой принцип разделения пригоден для тестов достижений, в которых обязателен ответ испытуемых на все пункты;
— распределением задач по времени решения каждой из частей (для тестов скорости).
Для испытуемых в выборке определения надежности (раздельно для каждой из частей теста) вычисляются оценки успешности решений, среднеквадратические отклонения первого и второго рядов оценок и коэффициенты корреляции сравниваемых рядов. Естественно, эти коэффициенты будут характеризовать надежность лишь половины теста.
Уравнение Спирмена—Брауна отражает влияние изменения количества заданий на коэффициент надежности теста:
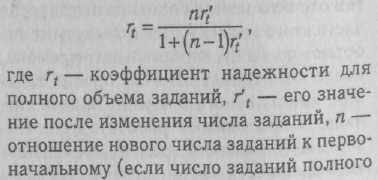
теста — 100, а его части, полученной методом расщепления на половины, — 50, то п = 0,5). Отсюда для полного теста;
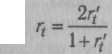
Приведенные формулы справедливы для случаев равных стандартных отклонений обеих половин теста (ох1= ах2). Если ах1 отличается от ах2, для определения "коэффициента надежности применяется формула Фланагана:

При определении г, целого теста можно воспользоваться формулой Рюлона:
rt = 1 j.
<*х
где о\ — дисперсия разностей между результатами каждого испытуемого по двум половинам теста, ах— дисперсия суммарных результатов. В данном случае коэффициент надежности рассчитывается как доля «истинной» дисперсии результатов теста (см. Надежность, Ошибка измерения).
При расщеплении тестов скорости применяется особая процедура группировки заданий. Определяется минимальное время ((т1п)'решения целого теста, затем отсчитываются половина и четвертая часть этого времени. Все испытуемые работают половину минимального времени, после чего ставят отметку против задания, выполняемого в момент подачи сигнала, и продолжают работать еще четверть минимального времени. Коэффициент надежности в этом случае будет соот-
ветствовать степени корреляции между числом задач, решенных до первого сигнала (0,5fmin) и решенных за время между первым и вторым сигналами (0,25*т| ).
Разделение заданий теста на равноценные половины является лишь частным случаем Н. ч. т. Вполне возможно расщепление на три, четыре и более частей. В предельном случае число частей равно числу пунктов. При этом для определения надежности применяют анализ внутренней согласованности.
При разделении всего набора заданий теста на любое количество групп для правильного определения Н. ч. т., как уже указывалось выше, должно соблюдаться требование равноценности таких групп. Поэтому при вычислении коэффициента надежности методом анализа внутренней согласованности отобранные задания теста должны быть в высокой степени однородны по содержанию и трудности (гомогенны). При гетерогенных задачах значения г, ниже истинных:
Наиболее распространенным методом оценки надежности отдельных заданий является вычисление коэффициента Кьюдера—Ричардсона:
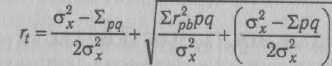

Это уравнение может быть упрошено следующим образом:
k
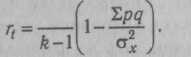
При отсутствии коэффициента дискриминации применим вариант формулы Кьюде ра—Рич ардс он а:
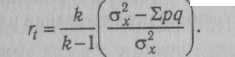
Пример вычислений rtno методу Кьюдера—Ричардсона приведен в табл. 17.
Предложенные выше формулы для определения коэффициента надежности пригодны для случаев, когда задания оцениваются в дихотомической шкале (см. Шкалы измерительные) по принципу «выполнено—не выполнено». Для случаев с более дифференцированной оценкой применима формула коэффициента альфа:
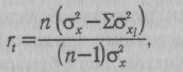
где £сг^. — сумма дисперсий результатов отдельных заданий.
В практике психологической диагностики считается, что тест надежен, если rt > 0,6.
Коэффициент надежности обладает доверительным интервалом, определение которого особенно важно в связи с большим количеством факторов, способных влиять на его значение. Доверительный интервал для г, определяется как

Таблица 17
|
|
|
 Скачать 5.87 Mb.
Скачать 5.87 Mb.