ТВиМС. Ответы по ТВиМС. Случайные события и предмет теории вероятностей

• Название: Случайные события и предмет теории вероятностей
• Анкор: ТВиМС
• Дата: 30.04.2023
• Размер: 1.02 Mb.
• Имя файла: Ответы по ТВиМС.docx
• Тип: Документы; #1098795
• страница: 3 из 6

20. Условный закон распределения системы С.В.

Если случайные величины, образующие систему, зависимы, то для нахождения закона распределения системы недостаточно знать законы распределения отдельных величин, входящих в систему. Требуется еще знать так называемый условный закон распределения одной из них.

Условным законом распределения одной из величин, входящих в систему, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение. Пусть случайная величина Y является дискретной.

Условной функцией распределения случайной величины X при условии называется условная вероятность события при условии события , т.е. .
Аналогично определяется условная функция распределения случайной величины Y при условии (когда случайная величина X является дискретной): .
21. Математическое ожидание и дисперсия системы случайных величин.

Математическим ожиданием двумерной случайной величины называется совокупность двух математических ожиданий М[Х], М[Y],то есть упорядоченных пар М[Х], М[Y],которые определяются равенствами:

а) если Х и Y– дискретные случайные величины:

М[Х]= , :  ;  .

М[Y]= .

б) если Х и Y– непрерывные случайные величины:

М[Х]=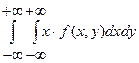

М[Y]= ,

где - плотность вероятности двумерной случайной величины .

Математическое ожидание случайной величины  , которая является функцией компонент  двумерной случайной величины  , находится аналогично по формулам:

1) М [j (Х, Y)] = 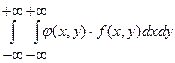- если Хи Y– непрерывные случайные величины;

2) М [j (Х, Y)] = , :  ;  - если Хи Y– дискретные случайные величины.

Дисперсиядвумерной случайной величины - совокупность двух дисперсий D[X] и D[Y], которые определяются равенствами:

а) если Х и Y– дискретные случайные величины:

D[X]= , :  ;  .

D[Y]=  .

б) если Х и Y– непрерывные случайные величины:

D[X]=

D[Y]= ,

где  - плотность вероятности двумерной случайной величины  ,

,  - математические ожидания компонент  .

22. Условное математическое ожидание системы С.В.

Пусть (X, Y) – система дискретных случайных величин. Условным математическим ожиданием дискретной случайной величины Y при условии, что Х= , называется величина

М[Y│X= ]= .

Аналогично, условным математическим ожиданием дискретной случайной величины X при условии, что Y=y_j, называется величина

М[Х│Y= ]= , :  ;  .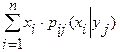

Пусть  - система непрерывных случайных величин. В этом случае условное математическое ожидание случайной величины Y при условии, что Х=x_i, определяется равенством:

М[Y│ ]= .

Аналогично, условное математическое ожидание случайной величины X при условии, что Y=y_j, определяется равенством:

М[Х│ ]=
23. Корреляционный момент и коэффициент корреляции.

Для характеристики связи между величинами Х и Y (22-й вопрос) служит корреляционный момент:

K_xy=М [ ]=M [(X – m_x) M (Y – m_y)].

Используя понятие корреляционного момента, запишем еще одно свойство дисперсии, а именно - дисперсия суммы двух случайных величин определяется равенством:

D[X+Y] = D[X]+D[Y]+2K_xy

Корреляционный момент иначе называется ковариация и обозначается cov(Х, Y).

Величина корреляционного момента вычисляется по формулам:

а) если Хи Y– дискретные случайные величины:

K_xy= , :  ;  .

б) если Хи Y– непрерывные случайные величины:

K_xy= ,

где  - плотность вероятности двумерной случайной величины  ,

,  - математические ожидания компонент  .

Корреляционный момент удобно вычислять по формуле:

K_xy=М[ХY]-М[Х]М[Y].

Если Хи Y независимы, то K_xy=0.Таким образом, если K_xy  0, то случайные величины Хи Y зависимы. В этом случае случайные величины Хи Y называются коррелированными.

Когда K_xy=0, случайные величины Хи Y называются некоррелированными.

Из рассмотренного свойства корреляционного момента получаем важное следствие. Дисперсия суммы двух случайных величин равна сумме их дисперсий если величины X и Y независимы, т.е.

D[X+Y] = D[X]+D[Y]+2K_xy

Коэффициент корреляции (r_xy)для двух случайных величин Хи Y есть безразмерная величина:

r_xy= ,

где , - средние квадратические отклонения величин Хи Y соответственно.



Коэффициент корреляции характеризует степень линейной зависимости двух случайных величин Х и Y.

24. Функции одной и двух случайных величин.

Функция одной случайной величины.

Свойства коэффициента корреляции.

1. r_xy Î [-1,1].

2. Если Хи Y независимы, то r_xy=0.

3. Если Хи Y связаны линейной зависимостью вида Y=а+b×X, то r_xy=1.

4. Если çr_xy ÷=1, то случайные величины Хи Y связаны линейной функциональной зависимостью:

прямой– если r_xy=1, обратной - если r_xy=-1.

Пусть рассматриваются две случайные величины Х и Y, которые связаны функциональной зависимостью вида Y=j (X).

Если Х– дискретная случайная величина, закон распределения которой определяется формулой

,

то случайная величина Y также дискретна, а её закон распределения выражается следующим образом:

, где y_i = φ(x_i), а  = .

Математическое ожидание и дисперсия случайной величины Y вычисляется по формулам:

для дискретной случайной величины

М[Y]=М [j (X)] = ,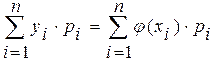

D[Y] = D [[j (X)] = Σ (y_i – m_y)² p_i = Σ (j (x_i) – m_y)² p_i

и для непрерывной случайной величины

М[Y]=М [j (X)] =

D[Y]=D [j (X)] = .

Функция двух случайных величин

Пусть рассматривается система двух случайных величин . Если каждой паре возможных значений случайных величин  соответствует одно возможное значение Z= , которое находится по определённому закону, то случайная величина Z называется функцией двух случайных аргументов .

Для функции двух и более случайных аргументов удобнее сначала находить функцию распределения G(z), а затем плотность вероятности g(z):

.

Если  - система дискретных случайных величин, то

, где  .

Если  - система непрерывных случайных величин, то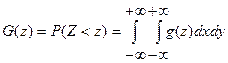

,

где  - плотность распределения случайной величины Z.

Важное значение имеет задача определения закона распределения суммы двух случайных величин: Z=Х+Y. Плотность распределения этой суммы равна:



или 

Если случайные величины Хи Yнезависимы, то  , и можно записать:

или где  ,  - плотности распределения случайных величин Хи Y.
25. Случайные функции. Математическое ожидание и дисперсия случайной функции и их свойства.
Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении t является случайной величиной. Если аргументом случайной функции является время, то случайная функция называется случайным процессом.

Математическим ожиданием случайной функции X(t) называют неслучайную функцию m_x(t), значение которой при каждом фиксированном значении аргумента равно математическому ожиданию сечения, соответствующего этому же значению аргумента:

m_x(t)=М[X(t)].
Свойство 1. Математическое ожидание неслучайной функции φ(t)(О равно самой неслучайной функции: М[φ(t)]=φ(t).

Свойство 2. Неслучайный множитель φ(t) можно выносить за знак математического ожидания: М[φ(t)Х(t)]=φ(t)М[X(t)]=φ(t)тx(t).

Свойство 3. Математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых: M[X(t)+Y(t)]=mx(t)+my(t).
Дисперсией случайной функции Х(t) называют неслучайную неотрицательную функцию Dx(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии сечения, соответствующего этому же фиксированному значению аргумента:

Dx(t)=D[X(t)].
Свойство 1. Дисперсия неслучайной функции φ(t) равна нулю: D[φ(t)]=0.
Свойство 2. Дисперсия суммы случайной функции Х(t) и неслучайной функции φ(t) равна дисперсии случайной функции: D[X(t)+φ(t)]=Dx(t).
Свойство 3. Дисперсия произведения случайной функции Х(t) на неслучайную функцию φ(t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции: D[X(t)φ(t)]=φ2(t)Dx(t).
26. Корреляционная функция случайной функции и ее свойства. Нормированная корреляционная функция.

Корреляционной функцией случайной функции Х(t)называют неслучайную функцию К_х(t₁,t₂) двух независимых аргументов t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:

К_х(t₁,t₂)=M[ (t₁)(t₂)].

Замечание. При равных между собой значенияхаргументов t₁=t₂=t корреляционная функция случайной функцииравна дисперсии этой функции: К_х(t,t)=D_x(t)

Действительно, учитывая, что D_x(t)=M[X(t)-m_x(t)]²=M[ (t)]², получим

К_х(t,t)= M[ (t)(t)]=М [ (t)]²=D_x(t).

Таким образом, достаточно знать корреляционную функцию, чтобы найти дисперсию случайной функции.

Свойство 1.При перестановке аргументов корреляционная функция не изменяется (свойство симметрии): К_х(t₁,t₂)= К_х(t₂,t₁).

Свойство 2.Прибавление к случайной функции Х(t) неслучайного слагаемого φ(t) не изменяет ее корреляционной функции: если Y(t)=X(t)+φ(t), то К_y(t₁,t₂)= К_х(t₁,t₂).

Свойство3.Приумножении случайной функции Х(t) нанеслучайный множитель φ(t)еекорреляционная функция умножается на произведение φ(t₁) φ(t₂):

если (t)= (t)φ(t). то К_y(t₁,t₂)= К_х(t₁,t₂) φ(t₁) φ(t₂).

Свойство 4.Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений: .
Нормированной корреляционной функцией случайной функции Х(t) называют неслучайную функцию двух независимых переменных t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:

 (*)

Учитывая, что  и  ,получим

 (*)

Таким образом, зная корреляционную функцию, можно найти нормированную корреляционную функцию.