ТВиМС. Ответы по ТВиМС. Случайные события и предмет теории вероятностей
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
27. Взаимные корреляционные функции двух случайных функций и их свойства. Нормированные взаимные корреляционные функции. Взаимной корреляционной функцией двух случайных функций Х(t) и Y(t) называют неслучайную функцию Rxy(t1,t2) двух независимых аргументов t1и t2 значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений обеих функций, соответствующих этим же фиксированным значениям аргументов: Rxy (t1, t2) = M[ (t1)(t2)]. Коррелированными называют две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю. Свойство 1.При одновременной перестановке индексов и аргументов взаимная корреляционная функция не изменяется:Rxy(t1,t2)= Ryx(t2,t1). Свойство 2.Прибавление к случайным функциям Х(t) и Y(t) неслучайных слагаемых, соответственно φ(t)и ψ(t), не изменяет их взаимной корреляционной функции: если X1(t)=X(t)+φ(t)и Y1(t)=Y(t)+ψ(t), то Rx1y2(t1,t2)= Rxy(t1,t2). Свойство 3.При умножении случайных функций Х(t)и У(t) на неслучайные множители, соответственно φ(t)и ψ(t), взаимная корреляционная функция умножается на произведениеφ(t1)ψ(t2): если X1(t)=X(t)φ(t)и Y1(t)=Y(t)+ψ(t), то Rx1y2(t1,t2)= Rxy(t1,t2) φ(t1)ψ(t). Свойство 4.Абсолютная величина взаимной корреляционной функции двух случайных функций не превышает среднего геометрического их дисперсий: Нормированной взаимной корреляционной функцией двух случайных функций Х(t) и Y(t)называют неслучайную функцию двух независимых аргументов t1и t2. 28. Стационарные случайные функции. Стационарнойназывают случайную функцию Х(t), математическое ожидание которой постоянно при всех значениях аргумента t и корреляционная функция которой зависит только от разности аргументов t2-t1. Из этого определения следует, что: 1) корреляционная функция стационарной случайной функции есть функция одного аргумента τ= t2-t1 т. е. Kx(t1,t2)=kx(t2-t1)=kx(τ);(*) 2) дисперсия стационарной случайной функции постоянна при всех значениях аргумента t и равна значению ее корреляционной функции в начале координат (τ=0), т.е. Dx(t)=Kx(t,t)=kx(t-t)= kx(0).(**) 29. Выборочный метод математической статистики. Выборочный метод – статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов. Совокупность исследуемых объектов, интересующих исследователя, называет генеральной совокупностью. А часть объектов, подлежащих изучению, называют выборочной совокупностью или выборкой. Необходимость выборочного метода может быть вызвана объективными причинами: - объект исследования очень обширный, например, исследование потребительских предпочтений на рынке продукта, прогноз результатов голосования на выборах и т.д. - необходимость в сборе первичной информации в «пилотных» исследованиях. Ключевые вопросы выборочного обследования: - количественная характеристика выборки или определение минимального количества наблюдений (объема выборки) для проведения исследования; - качественная характеристика выборки или способы и методы формирования выборочной совокупности. Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Существует 4 способа случайного отбора в выборку: 1. Случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы, и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел. 2. Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. 3. Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор. 4. Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение. Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная. При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку. Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку. Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор. 30. Свойства несмещенности, эффективности и состоятельности точечных оценок С.В. СВОЙСТВО НЕСМЕЩЕННОСТИ ОЦЕНКИ. Желательным требованием к оценке является отсутствие систематической ошибки, т.е. при многократном использовании вместо параметра θ его оценки Определение. Оценка Выборочное среднее арифметическое СВОЙСТВО СОСТОЯТЕЛЬНОСТИ ОЦЕНКИ. Второе требование к оценке — ее состоятельность — означает улучшение оценки с увеличением объема выборки. Определение. Оценка Сходимость по вероятности означает, что при большом объеме выборки вероятность больших отклонений оценки от истинного значения мала. СВОЙСТВО ЭФФЕКТИВНОЙ ОЦЕНКИ. Несмещенная оценка является эффективной, если она имеет наименьшую среди всех несмещенных оценок дисперсию. Это означает, что эффективная оценка обладает минимальным рассеиванием относительно истинного значения параметра. Заметим, что эффективная оценка существует не всегда, но из двух оценок обычно можно выбрать более эффективную, т.е. с меньшей дисперсией. Например, для неизвестного параметра a нормальной генеральной совокупности N(a,σ) в качестве несмещенной оценки можно взять и выборочное среднее арифметическое, и выборочную медиану. Но дисперсия выборочной медианы примерно в 1.6 раза больше, чем дисперсия среднего арифметического. Поэтому более эффективной оценкой является выборочное среднее арифметическое. 31. Точечные оценки параметров распределения, метод моментов и метод наибольшего правдоподобия. В статистике наиболее часто применяемые методы нахождения точечных оценок параметров распределения являются: - метод моментов (коротко (ММ); - метод максимального правдоподобия (коротко - ММП); - метод наименьших квадратов (коротко МНК). Суть метода моментов для нахождения точечных оценок неизвестных параметров заданного распределения состоит в том, что приравнивается теоретические моменты распределения соответствующим эмпирическим моментам, найденные по выборке. Например, если распределение зависит от одного параметра (задан вид плотности распределения где Если распределение зависит от двух параметров 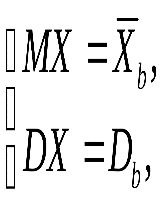 относительно параметров И, наконец, если надо оценить параметров (26) 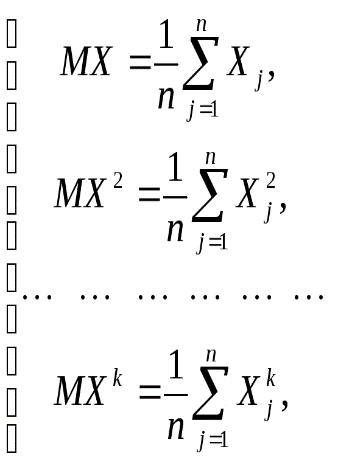 или или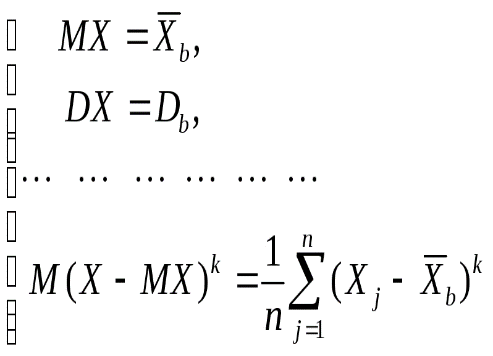 В этих системах мы видим, что присутствуют моменты до го порядков случайного события и его центрированного, Метод моментов является наиболее простым методом оценки параметров, и он был предложен в 1894г. Пирсоном. Оценки, получаемые методом моментов, обычно являются состоятельными, однако их эффективность часто меньше единицы. Метод максимального правдоподобия (ММП), предложен Р.Фишером в основе которого, лежит понятие так называемой функции «правдоподобия». Функцией правдоподобия, построенная по выборке (27) Функция правдоподобия обладает свойством «вполне мультипликативности» по аргументам (28) где За точечную оценку параметра , согласно ММП, берут такое его значение Такая оценка, называемая оценкой максимальной правдоподобия, является решением уравнения (29) Из курса математического анализа известно, что функции Таким образом, для нахождения оценки максимального правдоподобия необходимо: 1. решить уравнение правдоподобия (30) 2. следует отобрать то решение, которое обращает функцию (31) то точкой максимума будет В случаях, когда подлежат оценке несколько параметров  |
