ТВиМС. Ответы по ТВиМС. Случайные события и предмет теории вероятностей

• Название: Случайные события и предмет теории вероятностей
• Анкор: ТВиМС
• Дата: 30.04.2023
• Размер: 1.02 Mb.
• Имя файла: Ответы по ТВиМС.docx
• Тип: Документы; #1098795
• страница: 5 из 6

32. Метод наименьших квадратов.

Имеются результаты  независимых измерений - опытные точки Из теоретических или иных соображений, с точностью до количества (или других признаков) неизвестных параметров (здесь мы ограничимся двумя) и известна функциональная зависимость от в виде

(35)  .

Экспериментальные точки уклоняются от этой зависимости вследствие неизбежных ошибок измерений. Как правило, эти ошибки распределены по нормальному закону. Рассмотрим некоторое значение независимой переменной  . Результат измерения может рассматриваться как нормально распределённая случайная величина с математическим ожиданием и с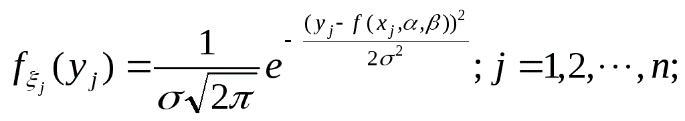оответствующим среднеквадратичным отклонением , характеризующим ошибку измерений. Дополнительно предположим, что «точность измерения во всех точках одинакова, то есть Тогда плотность вероятности с.в. имеет вид

(36) 

В результате получаем  мерную случайную величину , ко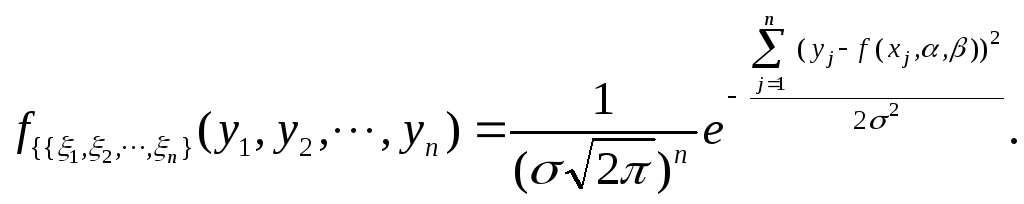ординаты которой независимы и плотности вероятности которых определении равенствами (36). Как было показано ранее, плотность распределения системы независимых случайных величин равна произведению плотностей вероятности компонент:

(37) 

Теперь для определения параметров  и воспользуемся идеей метода максимального правдоподобия (ММП), согласно которой в эксперименте реализуются те значения компонент, при которых плотность вероятности системы (37), близка к максимальному значению. Учитывая специальный вид равенств (37), можно заметить, что она достигает максимума, когда показатель степени принимает максимальное значения. Отбрасывая отрицательный множитель приходим к задаче отыскания минимума выражения:

(38)  .

Поскольку минимизируется сумма квадратов разностей экспериментальных и теоретических значений функции (их обычно называют «невязками»), предложенную процедуру называют методом наименьших квадратов.

Согласно теории дифференциального исчисления в принципе задача сводится к решению

системы двух однородных дифференциальных уравнений в частных производных:

(39)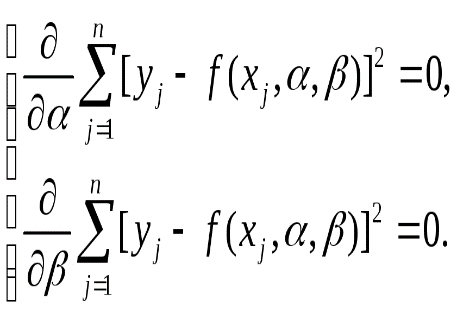 

Если функциональная зависимость (35) линейна относительно параметров  и , то система уравнений (39) также будет линейной и её решение можно найти известными методами линейной алгебры.

Таким образом, в общем случае мы приходим к следующему выводу.

Метод нахождения оценки  неизвестного параметра , основанный на минимизации суммы квадратов отклонений выборочных данных от определяемой (искомой) оценки называется методом наименьших квадратов.

Другими словами, в МНК требуется найти такое значение , которое минимизировало бы сумму


33. Распределение выборочных характеристик. Распределение выборочного среднего при неизвестной и известной дисперсии. Распределение выборочной дисперсии.




4.3.1. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНОГО СРЕДНЕГО ПРИ ИЗВЕСТНОЙ ДИСПЕРСИИ

Рассмотрим выборочное среднее выборки из N независимых наблюдений случайной величины х: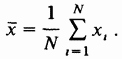



Cреднее значение выборочного распределения величины х равно

Дисперсия выборочного распределения величины х есть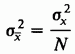



Следовательно, в силу распределения обеих частей следующего соотношения, содержащего х, совпадают: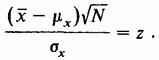



Поэтому относительно возможных значений выборочного среднего можно утверждать, что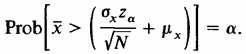


34. Интервальные оценки. Доверительный интервал, доверительная вероятность.
Интервальной называют оценку, которая определяется двумя числами – началом и концом интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть    — это оценка неизвестного оцениваемого параметра   . Пусть    — это некоторое положительное число. Если выполняется неравенство  ,то говорят, что интервал    покрывает неизвестный параметр   .
Доверительным интервалом называют найденный по данным выборки интервал   , который покрывает неизвестный параметр    с заданной надежностью   . Надежность    задается по условию задачи и обычно принимается равной 0,95, или 0,99, или 0,999.
Вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надежными (достоверными), называют доверительной вероятностью или надежностью. Величина доверительной вероятности определяется характером производимых измерений. При выполнении учебных лабораторных работ в курсе общей физики доверительная вероятность обычно считается равной 95 %.
35. Вариационный ряд. Таблица частот. Гистограмма.
Вариационный ряд — это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака. Например, больных по возрасту, по срокам лечения, новорожденных по весу и т.п.
Наиболее естественной формой эмпирического закона распределения является так называемая таблица частот (относительных частот), в первой строке которой записываются числа вариационного ряда, а во второй –– соответствующие им частоты n і (относительные частоты w і). Сумма всех частот равна объему выборки п, а сумма всех относительных частот равна единице.
Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которой служат частичные интервалы длины h, а высоты равны nj.

Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высотами – относительные частоты ωj.
36. Проверка статистических гипотез.

Под статистической гипотезой или просто гипотезой понимают всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Статистические гипотезы служат инструментом проверки выдвигаемых теоретических предположений. Гипотезы могут быть высказаны относительно параметров статистического распределения вероятностей. Например, в случае нормального закона распределения с.в., относительно м.о. и дисперсии. Тогда гипотезу называют параметрической.

Предположения могут быть сделаны так же относительно самого распределения с.в. (подчинение закону Бернулли, Пуассона, геометрическому, равномерному, нормальному и т.д.). В этом случае проверяемую гипотезу называют непараметрической.

На практике одну из гипотез выделяют в качестве основной или нулевой и обозначают , (которая формируется в предположении отсутствия существенной различии между выборочной и генеральной совокупностями), а другую конкурирующей гипотезы, являющуюся противоположной к , т.е. логическим отрицанием первого, в качестве альтернативной гипотезы и обозначается.

Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой, если в ней идёт речь об одном значении параметра, в противном случае –сложной.

Например, гипотеза  , состоящая в том, что математическое ожидание с.в. равно , то есть , является простой. В качестве альтернативной гипотезы, т.е. сложной можно рассматривать одну из следующих гипотез: или , .

Имея две гипотезы  и надо на основе выборки , принять либо основную гипотезу , либо конкурирующую . Исследуя выборку, принимается решение: согласуется она с этой гипотезой или нет. Альтернативная гипотеза принимается после того, как опровергается основная (нулевая).

Правило, по которому принимается решение принять или отклонить гипотезу  , или отклонить или принять , называется статистическим критерием или просто критерием проверки данной гипотезы.

Проверку гипотез осуществляют на основании результатов выборки  , из некоторых формируют функцию выборки , называемой статистикой критерия.

Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия разбивается на два непересекающихся подмножества: критическую область т.е. область отклонения гипотезы и область принятия гипотезы  . Если фактически наблюдаемое значение статистики критерия, т.е. значение критерия, вычисленное по выборке: попадает в критическую область то основная гипотеза отклоняется и принимается альтернативная гипотеза ; если же попадает в область , то принимается , а отклоняется.

37. Проверка гипотезы о равенстве средних двух нормальных распределений с известными и неизвестными дисперсиями

Пусть X и Y – нормальные генеральные совокупности с известными генеральными дисперсиями σ_x² и σ_y² и неизвестными математическими ожиданиями μ_x и μ_y . Из генеральных совокупностей взяты две независимые выборки объёмами n_x и n_y и вычислены выборочные средние арифметические   и   . Для проверки гипотезы о равенстве генеральных средних H₀: μ_x = μ_y используют статистический критерий: 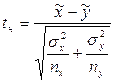  , который при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения N(0;1).

Выбор критической области зависит от содержания конкурирующей гипотезы H₁. Согласно требованию к критической области при H₁: μ_x > μ_y выбирают правостороннюю, при H₁: μ_x < μ_y – левостороннюю, а при             H₁: μ_x ≠ μ_y – двустороннюю критические области.

Границы критических областей при заданном уровне значимости α находят по интегральной функции Лапласа из условия Ф(t_кр) = 1 – 2α (для правосторонней и левосторонней критических областей) и условия      Ф(t_кр) = 1 – α (для двусторонней критической области).

Проверка гипотезы сводится к следующему: если |t_н| > t_кр, нулевая гипотеза H₀ отвергается с вероятностью ошибки α, если |t_н| ≤ t_кр, то делается вывод, что нулевая гипотеза не противоречит опытным данным.

При неизвестных генеральных дисперсиях либо требуется достаточно большой объём выборки для надёжной и точной оценки, либо требуется, чтобы эти дисперсии были одинаковы (σ_x² = σ_y²), в противном случае известные критерии малоэффективны.

Если из двух генеральных совокупностей взяты две случайные независимые выборки со средними значениями   ,   и выборочными дисперсиями S_x², S_y², то для проверки гипотезы H₀: μ_x = μ_y используют статистику   , имеющую распределение Стьюдента с k = n_x + n_y – 2 степенями свободы. Вид критической области зависит, как обычно, от конкурирующей гипотезы: при H₁: μ_x > μ_y выбирают правостороннюю, при H₁: μ_x < μ_y – левостороннюю, а при H₁: μ_x ≠ μ_y – двустороннюю критические области.

Границы критической области (t_кр) находят по таблице распределения Стьюдента при двусторонней симметричной критической области для заданного уровня значимости α, а при правосторонней и левосторонней критических областях при 2α и числе степеней свободы k = n_x + n_y – 2.

Правила проверки гипотезы H₀: μ_x = μ_y такие же, как у гипотезы            H₀: μ = μ₀. Гипотеза H₀ отвергается при |t_н| > t_кр.
38. Двухвыборочный t-тест с одинаковыми и различными дисперсиями.

На основе t-теста строится процедура проверки гипотез о равенстве средних (математических ожиданий) двух независимых нормальных распределений с неизвестными дисперсиями и.

Относительно дисперсий и можно выдвинуть следующие два предположения:

1. 
   Обе дисперсии неизвестны, но предполагается, что они равны между собой, т.е. = .
   
2. 
   Обе дисперсии неизвестны и предполагается, что они не равны между собой, т.е. ≠ .
   

В случае когда обе дисперсии неизвестны, но предполагается что они равны между собой, мы имеем дело с двумя оценками   и   одной и той же дисперсии = . в этом случае строится объединённая оценка :

 ,

S²- это объединённая оценка дисперсии   = = .

В математической статистике доказывается, что если нулевая гипотеза о равенстве математических ожиданий H₀: m_x=m_y выполняется, то величина t вычисляется по формуле:



где и   - средние арифметические величины,

n₁ – число наблюдений в первой выборке,

n₂- число наблюдений во второй выборке,

S – выборочное стандартное отклонение,

 .

Статистика t имеет распределение Стьюдента. Число степеней свободы определяется по формуле:



Эту t-статистику и используют в качестве критерия при проверке нулевой гипотезы о равенстве математических ожиданий. Схема проверки аналогична проверке при использовании Z-теста.

• 
  В случае, когда дисперсии неизвестны и предполагается, что они не равны, используется аналог Z-теста с заменой дисперсий их оценками.
  

 — это распределение близко распределению Стьюдента. Число степеней свободы вычисляется по следующей формуле:



В данном случае t-статистику, используемую для проверки нулевой гипотезы о равенстве средних величин при различных неизвестных дисперсиях, называют критерием Фишера-Беренса.