ТВиМС. Ответы по ТВиМС. Случайные события и предмет теории вероятностей

• Название: Случайные события и предмет теории вероятностей
• Анкор: ТВиМС
• Дата: 30.04.2023
• Размер: 1.02 Mb.
• Имя файла: Ответы по ТВиМС.docx
• Тип: Документы; #1098795
• страница: 6 из 6

39. Двухвыборочный F-тест для дисперсий.

В математической статистике доказывается, что если гипотеза о равенстве дисперсий двух случайных величин выполняется: H₀: =, то величина   распределена в соответствии с законом распределения Фишера.

Это отношение F называют дисперсионным отношением Фишера и используют в качестве критерия проверки нулевой гипотезы.

Распределение Фишера характеризуется наличием степеней свободы, которые вычисляются по формулам:



Поскольку величина F - неотрицательная, то критическая область данной величины будет принадлежать интервалу (0;+).

Альтернативными гипотезами являются гипотезы:

Н₁: > при >

Н₁: < при <

Последовательность проверки гипотезы:

1. 
   Производится расчёт F-статистики Фишера.
   
2. 
   Задаёмся уровнем значимости, который находится в пределах от 0,01 до 0,05.
   
3. 
   Вычисляется число степеней свободы: df₁ , df₂ .
   
4. 
   Находим критическое значение F_крравное F _,df1,df2, используя таблицы, либо с помощью функции FРАСПОБР.
   
5. 
   Сравниваем рассчитанное значение значения F-статистики и критическое: если F_расч >F_кр , то гипотеза отвергается.
   

40. Парный двухвыборочный t-тест для средних значений.

Парный двухвыборочный t-тест для средних значений позволяет оценить разность между математическими ожиданиями двух генеральных совокупностей, связанных между собой, когда показатели первой группы зависят от показателей другой. Использование этого теста часто применяются для того, чтобы обнаружить результат какого-либо воздействия или, наоборот, доказать отсутствие этого воздействия. Чем более однородными окажутся выбранные для эксперимента объекты, чем меньше их различия, тем точнее будет ответ на вопрос о том, имеет ли место какое либо воздействие на результат или нет.

Различия между объектами, выбранными для обнаружения воздействия некоторого фактора на результат, будет меньше, если для воздействия и контроля выступает один и тот же объект.

Пусть х_i и у_i - результаты измерения для объекта i, где 1£ i£ n, тогда совокупность случайных величин: {(х₁,у₁), …, (х_n,y_n)} образует парные данные. Все наблюдения считаются реализациями случайных величин X, Y. При этом предполагается, что для двух разных объектов они независимы. Однако наблюдения, входящие в одну пару нельзя считать независимыми, т.к. они относятся к одному объекту и, следовательно, они отражают свойства общего объекта и могут зависеть друг от друга. Поэтому, для того, чтобы характеризовать пару наблюдений (х_i , у_i )вводится новая случайная переменная  . Эту переменную можно считать независимой и нормально распределённой случайной величиной.

Таким образом, задача о парных данных сводится к задаче об одной нормальной выборке при неизвестной дисперсии  .

При неизвестной дисперсии  гипотеза выглядит следующим образом:

Н₀: m_d=a₀ , где m_d = m_x – m_y –это математическое ожидание случайной величины d, a₀ –заранее заданное число - гипотетическая разность, равная в данном случае нулю.

Для проверки этой гипотезы используется t-критерий, который вычисляется по формуле:

,

где

.

t-критерий имеет распределение Стьюдента с числом степеней свободы df=n-1.

Для проверки гипотезы о различиях между средними используется инструмент анализа «Парный двухвыборочный t-тест для средних» на основе парных выборочных данных. При этом равенства дисперсий генеральных совокупностей не предполагается. В диалоговом окне задаются интервалы переменной 1 и переменной 2, гипотетическая разность, равная нулю.

Если дисперсия случайной величины D известна, то можно использовать аналог z – критерия



который имеет нормальное распределение.
41. Однофакторный дисперсионный анализ.
Простейшим случаем дисперсионного анализа является одномерный однофакторный анализ для двух или нескольких независимых групп, когда все группы объединены по одному признаку. В ходе анализа проверяется нулевая гипотеза о равенстве средних. При анализе двух групп дисперсионный анализ тождественен двух выборочному t-критерию Стьюдента для независимых выборок, и величина F-статистики равна квадрату соответствующей t-статистики.

Для подтверждения положения о равенстве дисперсий обычно применяется критерий Ливена (Levene’s test). В случае отвержения гипотезы о равенстве дисперсий основной анализ неприменим. Если дисперсии равны, то для оценки соотношения межгрупповой и внутригрупповой изменчивости применяется F-критерий Фишера:

{\displaystyle F_{df_{\textrm {bg}},df_{\textrm {wg}}}={\frac {MS_{\textrm {bg}}}{MS_{\textrm {wg}}}}.}

Если F-статистика превышает критическое значение, то нулевая гипотеза не может быть принята (отвергается) и делается вывод о неравенстве средних. При анализе средних двух групп результаты могут быть интерпретированы непосредственно после применения критерия Фишера.

При наличии трёх и более групп требуется попарное сравнение средних для выявления статистически значимых отличий между ними. Априорный анализ включает метод контрастов, при котором межгрупповая сумма квадратов дробится на суммы квадратов отдельных контрастов:{\displaystyle SS_{\textrm {bg}}=SS_{\psi _{1}}+SS_{\psi _{2}}+…+SS_{\psi _{n}},}



где  {\displaystyle \psi } есть контраст между средними двух групп, и затем при помощи критерия Фишера проверяется соотношение среднего квадрата для каждого контраста к внутригрупповому среднему квадрату:

{\displaystyle F_{1,df_{\textrm {wg}}}={\frac {MS_{\psi _{i}}}{MS_{\textrm {wg}}}}.}

Апостериорный анализ включает post-hoc t-критерии по методам Бонферрони или Шеффе, а также сравнение разностей средних по методу Тьюки. Особенностью post-hoc-тестов является использование внутригруппового среднего квадрата {\displaystyle MS_{\textrm {wg}}}  для оценки любых пар средних. Тесты по методам Бонферрони и Шеффе являются наиболее консервативными, так как они используют наименьшую критическую область при заданном уровне значимости {\displaystyle \alpha }

Помимо оценки средних дисперсионный анализ включает определение коэффициента детерминации {\displaystyle R^{2}} , показывающего, какую долю общей изменчивости объясняет данный фактор:
42. Выявление отличающихся друг от друга групп с помощью процедура Тьюки – Крамера

Этот метод является примером процедур апостериорного сравнения (post hoc comparison), поскольку проверяемая гипотеза формулируется после анализа данных. Процедура Тьюки-Крамера позволяет одновременно сравнить все пары групп. На первом этапе вычисляются разности X_j– X_j’, где j ≠j’, между математическими ожиданиями с(с – 1)/2 групп. Критический размах процедуры Тьюки-Крамера вычисляется по формуле: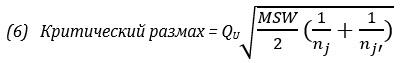



где Q_U — верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и n– с степеней свободы в знаменателе.

Если объемы выборок не одинаковы, критический размах вычисляется для каждой пары математических ожиданий отдельно. На последнем этапе каждая из с(с – 1)/2 пар математических ожиданий сравнивается с соответствующим критическим размахом. Элементы пары считаются значимо различными, если модуль разности |X_j– X_j’| между ними превышает критический размах.

43. Проверка равенства дисперсий с помощью модифицированного критерия Левенэ.

Несмотря на то что F-критерий относительно устойчив к нарушениям условия о равенстве дисперсий в группах, грубое нарушение этого предположения существенно влияет на уровень значимости и мощность критерия. Возможно, одним из наиболее мощных является критерий Левенэ. Для проверки равенства дисперсий с генеральных совокупностей проверим следующие гипотезы:

Н₀: σ₁²= σ₂²= … = σ_j²

Н₁: не все σ_j²одинаковы (j = 1, 2, …, с)

Модифицированный критерий Левенэ основан на утверждении, что если изменчивость в группах одинакова, для проверки нулевой гипотезы о равенстве дисперсий можно применить анализ дисперсии абсолютных величин разностей между наблюдениями и медианами групп. Итак, сначала следует вычислить абсолютные величины разностей между наблюдениями и медианами в каждой группе, а затем выполнить однофакторный дисперсионный анализ полученных абсолютных величин разностей.
44. Двухфакторный дисперсионный анализ без повторений и с повторениями

Двухфакторный дисперсионный анализ без повторений:

Двухфакторный дисперсионный анализ применяется для того, чтобы проверить возможную зависимость результативного признака от двух факторов - A и B. Тогда a - число градаций фактора A и b - число градаций фактора B. В статистическом комплексе сумма квадратов остатков разделяется на три компоненты:

SS = SSa + SSb + SSe,

где

 - общая сумма квадратов отклонений,

 - объяснённая влиянием фактора A сумма квадратов отклонений,

 - объяснённая влиянием фактора B сумма квадратов отклонений,

 - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки,

 - общее среднее наблюдений,

 - среднее наблюдений в каждой градации фактора A,

 - среднее число наблюдений в каждой градации фактора B.

Дисперсии вычисляются следующим образом:

 - дисперсия, объяснённая влиянием фактора A,

 - дисперсия, объяснённая влиянием фактора B,

 - необъяснённая дисперсия или дисперсия ошибки,

где

va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,

vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,

ve = (a − 1)(b − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,

v = ab − 1 - общее число степеней свободы.

Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:

для фактора A:

H0: μ1A = μ2A = ... = μaA,

H1: не все μiA равны;

для фактора B:

H0: μ1B = μ2B = ... = μaB,

H1: не все μiB равны.

Чтобы определить влияние фактора A, нужно фактическое отношение Фишера   сравнить с критическим отношением Фишера  .

Чтобы определить влияние фактора B, нужно фактическое отношение Фишера   сравнить с критическим отношением Фишера  .

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.

Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.
Двухфакторный дисперсионный анализ с повторениями:

Двухфакторный дисперсионный анализ с повторениями применяется для того, чтобы проверить не только возможную зависимость результативного признака от двух факторов - A и B, но и возможное взаимодействие факторов A и B. Тогда a - число градаций фактора A и b - число градаций фактора B, r - число повторений. В статистическом комплексе сумма квадратов остатков разделяется на четыре компоненты:

SS = SSa + SSb + SSab + SSe,

где

 - общая сумма квадратов отклонений,

 - объяснённая влиянием фактора A сумма квадратов отклонений,

 - объяснённая влиянием фактора B сумма квадратов отклонений,

 - объяснённая влиянием взаимодействия факторов A и B сумма квадратов отклонений,

 - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки,

 - общее среднее наблюдений,

 - среднее наблюдений в каждой градации фактора A,

 - среднее число наблюдений в каждой градации фактора B,

 - среднее число наблюдений в каждой комбинации градаций факторов A и B,

n = abr - общее число наблюдений.

Дисперсии вычисляются следующим образом:

 - дисперсия, объяснённая влиянием фактора A,

 - дисперсия, объяснённая влиянием фактора B,

 - дисперсия, объяснённая взаимодействием факторов A и B,

 - необъяснённая дисперсия или дисперсия ошибки,

где

va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,

vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,

vab = (a − 1)(b − 1) - число степеней свободы дисперсии, объяснённой взаимодействием факторов A и B,

ve = ab(r − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,

v = abr − 1 - общее число степеней свободы.

Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются три нулевые гипотезы и соответствующие альтернативные гипотезы:

для фактора A:

H0: μ1A = μ2A = ... = μaA,

H1: не все μiA равны;

для фактора B:

H0: μ1B = μ2B = ... = μaB,

H1: не все μiB равны;

для взаимодействия факторов A и B:

H0: ABij = 0,

H1: ABij ≠ 0 для всех i и j.

Чтобы определить влияние фактора A, нужно фактическое отношение Фишера   сравнить с критическим отношением Фишера  .

Чтобы определить влияние фактора B, нужно фактическое отношение Фишера   сравнить с критическим отношением Фишера  .

Чтобы определить влияние взаимодействия факторов A и B, нужно фактическое отношение Фишера   сравнить с критическим отношением Фишера  .

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.

Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.