ИДЗ. Случайные события
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Индивидуальные задания по Вероятность и статистика (2020-2021уч.г.)
Замечание: Если студент в журнале №12, тогда он выполняет №12 из 1.1; №12 из 1.2; №12 из 2; №12 из 3; №12 из 4; 1.1 СЛУЧАЙНЫЕ СОБЫТИЯ 1. В группе из 30 учеников на контрольной работе 6 учеников получили оценку «отлично», 10 учеников «хорошо», 9 учеников «удовлетворительно». Какова вероятность того, что все три вызванных к доске ученика, имеют неудовлетворительные оценки по контрольной работе. 2. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна восьми, а разность четырем. б) сумма выпавших очков равна восьми, если известно, что их разность равна четырем. 3. В коробке содержится 6 одинаковых занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке. 4.Какова вероятность того, что в январе, наудачу взятого года окажется 4 воскресенья. Из партии, в которой 31 деталь без дефектов и 6 с дефектом, берут наудачу 3 детали. Чему равна вероятности следующих событий: а) все три детали без дефектов; б) две детали без дефектов; в) хотя бы одна деталь без дефекта. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится герб. В мешочке имеются 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из букв: О, П, Р, С, Т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию»-кубиках можно будет прочесть слово «СПОРТ». На каждый из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной и выложенных в ряд карточек можно будет прочесть слово «трос». Куб, все грани которого окрашены, распилен на тысячу кубиков одного размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приложить к первой, если первая кость: а) оказалась дублем; б) не дублем. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть. Из колоды в 36 карт наугад выбирают 3 карты. Какова вероятность того, что среди них окажется два туза. Колода из 36 карт разделена наудачу на две равные части. Найти вероятность того, что каждая из полу колод будет одной масти. Восемь различных книг расставляют наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом. Библиотека состоит из 10 различных книг, причем 5 книг стоят по 400 сум каждая, три книги по 100 сум, две книги по 300 сум. Найти вероятность того, что взятые наудачу две книги стоят 500 сум. В цехе работают 6 мужчин и 4 женщины. По талонным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц, окажутся 3 женщины. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных 5 отличников. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие. Из полного набора домино (28 штук) наудачу выбирают 7 костей. Какова вероятность, что среди них окажется хотя бы одна кость с шестью очками. Из колоды в 52 карты извлекают наудачу 4 карты. Найти вероятности следующих событий: А = {в полученной выборке все карты бубновой масти}; В = {окажется хотя бы один туз}. Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если число мест равно 8. Бросается 10 одинаковых игральных костей. Вычислить вероятность следующих событий А = {ни на одной кости не выпадет 6 очков}; В = {хотя бы на одной кости выпадет 6 очков}; С – {равно на 3 костях выпадет 6 очков}. Собрание из 25 человек, среди которых 5 женщин, выбирает наудачу 3 делегатов на конференцию. Найти вероятность того, что в состав делегации вошли 2 женщины и 1 мужчина. Опыт состоит в четырехкратном выборе с возвращением одной из букв среди имеющихся: {а, б, к, о, м} и выкладывании слова в порядке поступления букв. Какова вероятность, что в результате будет выложено слово "мама"? Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников, 7 третьекурсников. Из этого состава наудачу выбирают пять человек на предстоящую конференцию. Найти вероятности следующих событий: а) будут отобраны одни третьекурсники; б) все первокурсники попадут на конференцию; в) не будет выбрано ни одного второкурсника. Два равных противника играют матч из п партий в теннис. Каждая партия заканчивается выигрышем, либо проигрышем одного из участников. Все исходы данного матча равновероятны. Найти вероятность того, что первый игрок выиграет равно m партий (m ≤ n). Из 60 заданных вопросов студент знает ответ на 50. Найти вероятность того, что студент ответит на все три заданных ему вопроса. На отдельных карточках написаны цифры I, 2, 3, 4, 5, 6, 7, 8, 9, карточки тщательно перемешаны. Наудачу извлечены 4 карточки и выложены в ряд. Найти вероятность тою, что они составили число 1234. 1.2. СЛУЧАЙНЫЕ СОБЫТИЯ 1. Студент знает 20 вопросов из 25. Найти вероятность того, что из наудачу заданных ему 3 вопросов он ответит на все три. 2. В ящике содержится 10 пронумерованных кубиков. Наудачу взято три кубика. Найти вероятность того, что последовательно появились кубики с номерами 1,2,3 , если кубики извлекались: а) с возвращением; б) без возвращения. 3. Для некоторой местности среднее число пасмурных дней в июле равно шести. Найти вероятность того, что первого и второго июля будет ясная погода. 4.В группе 10 студентов, из них 7 отличников. Четверых студентов вызвали в деканат. Найдите вероятность того, что все вызванные студенты являются отличниками. 5.Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из 5 взятых изделий 3 высшего сорта. 6.В первом ящике содержится 4 белых и 8 красных шаров. Во втором ящике 10 белых и 6 красных. Из каждого ящика взято по одному шару. Найти вероятность того, что оба взятых шара белого цвета. 7.В цехе работают 7 мужчин и 8 женщин. По табельным номерам наудачу отобрано три человека. Какова вероятность того, что все отобранные лица окажутся женщинами? 8.В первом ящике 5 белых и 10 черных шаров. Во втором ящике 10 белых и 5 черных шаров. Из каждого ящика взято по одному шару. Какова вероятность того, что хотя бы один из взятых шаров белый? 9.Вероятность того, что в течение смены станок выйдет из строя равна 0,05. Найти вероятность того, что в течение трех смен станок будет работать исправно. 10.Монета бросается до первого выпадения герба. Найти вероятности того, что число бросаний монеты будет четным числом. 11. В ящике содержится 12 деталей, изготовленных на первом заводе, 20 деталей второго завода 18 деталей третьего завода. Вероятность того, что деталь первого завода отличного качества равна 0,9. Для второго и третьего заводов эта вероятность соответственно 0,6 и 0,9. Найдите вероятность того, что наудачу взятая деталь отличного качества. 12. В первой урне 10 шаров, из них 8 белых. Во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу взято по одному шару, затем из этих двух шаров снова наудачу взят один шар. Найти вероятность того, что этот шар оказался белым. 13.В каждой из трех урн содержится 6 черных, 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны извлечен один шар и переложен в третью урну. Найти вероятность того, что наудачу извлеченный из третьей урны шар окажется белым. 14.Вероятности того, что во время работы электронной машины произойдет сбой в арифметическом устройстве , в оперативной памяти , в остальных устройствах относятся как 3:2:5 . Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен. 15.В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. 16. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу проезжающих по этому шоссе легковых автомобилей как 3:2. Вероятность того, что будет заправляться грузовая машина равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина. 17.В специализированную больницу поступают в среднем 50% больных с заболеванием К, 20% с заболеванием М, 30% с заболеванием L. Вероятность полного излечения болезни К равна 0,7, для болезней L и М эти вероятности равны соответственно 0,8 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К. 19. Имеется две урны с шарами. В первой урне 2 белых и 1 черный шар, во второй 1 белый и 4 черных шара. Наудачу выбрана одна урна и из нее извлечен один шар. Найти вероятность того, что взят белый шар. 20. В урне содержалось 20 шаров, из которых 12 черных и 8 белых. Один шар потерялся. Из остальных 19 шаров наудачу извлекли один шар. Найти вероятность того, что взят шар черного цвета. 21. В двух одинаковых урнах содержатся шары. В первой урне 3 белых и 2 черных, во второй 4 белых и 4 черных. Из первой урны во вторую переложено два шара. Затем из второй урны взят один шар. Найти вероятность того, этот шар белого цвета. 22. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0.8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы. 23. Устройство состоит из 8 независимо работающих элементов. Вероятность отказов каждого из элементов за время t одинакова и равна 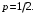 Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента из восьми. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента из восьми.24. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырех или три партии из шести (ничьи во внимание не принимаются). 25. Монета брошена 10 раз. Найти вероятность выпадение герба: а) от 4 до 6 раз; б) хотя бы один раз. 26. Два равносильных противника играют в шахматы. Что вероятнее выиграть: а) одну партию из двух или две из четырех; б) не менее двух партий из четырех или не менее трех партий из пяти. 27. В семье 5 детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0.51. 28. Продукция предприятия содержит в среднем 5% брака. Найти вероятность того, что из 5 проверенных изделий 2 оказались бракованными. 29. На автобазе имеются 8 машин. Вероятность выхода каждой из них равна 0.8. Найти вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не менее шести автомашин. 30. Вероятность того, что телевизор потребует ремонта в течение гарантийного срока равна 0.2. Найти вероятность того, что из шести телевизоров не более одного потребует гарантийного ремонта. 2.СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 1. В ящике содержится 5 белых и 25 черных шаров. Из ящика взят один шар. Случайная величина X - число взятых белых шаров. Составить закон распределения случайной величины X. 2. В ящике содержится 10 деталей, из них 8 - стандартных. Наудачу взято 2 детали. Составьте закон распределения числа стандартных деталей среди взятых. 3. Дискретная случайная величина X задана законом распределения:
Постройте многоугольник распределения. 4. Составьте закон распределения случайной величины X - числа выпадений герба при двукратном подбрасывании монеты. 5. Две игральные кости одновременно бросают 2 раза: а) написать биноминальный закон распределения дискретной случайной величины X - числа выпадений четного числа очков на двух игральных костях; б) построить многоугольник распределения. 6. Два стрелка одновременно стреляют по мишени и делают по одному выстрелу. Вероятность попадания в цель для первого стрелка равна 0,5; для второго 0,4. Дискретная величина X - число попаданий в цель: а) составьте закон распределения дискретной случайной величины X; б) постройте многоугольник распределения. | ||||||||||||||||||||||||||||||||||||||||

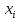 a)
a)