Девятко И. Ф. Методы социологического исследования. Екатеринбург, Изд-во Урал, ун-та, 1998. 208 с. Девятко И. Ф. Методы социологического исследования. Екатеринбург. Социологического исследования екатеринбург Издательство Уральского университета

• Название: Социологического исследования екатеринбург Издательство Уральского университета
• Анкор: Девятко И. Ф. Методы социологического исследования. Екатеринбург, Изд-во Урал, ун-та, 1998. 208 с.doc
• Дата: 27.05.2017
• Размер: 1.7 Mb.
• Имя файла: Девятко И. Ф. Методы социологического исследования. Екатеринбург.doc
• Тип: Книга; #8072
• Категория: Социология. Политология
• страница: 6 из 28

ГЛАВА 4. ЭКСПЕРИМЕНТ В СОЦИАЛЬНЫХ

НАУКАХ

Эксперимент — это опытное исследование воздействия отдельного фактора (или нескольких факторов) на интересующую исследователя переменную. Экспери­ментальное исследование строится в соответствии с правилами индуктивного вывода о наличии причинно-следственной связи между событиями, во-первых, демонстрируя регулярный характер появления события-«отклика» после пред­шествующего по времени события-воздействия и, во-вторых, исключая посред­ством особых приемов экспериментальной изоляции и контроля альтернативные объяснения появления «отклика» с помощью посторонних влияний и кон­курирующих каузальных гипотез¹. Соответственно данные экспериментального исследования представляют собой наилучшее приближение к модели статистического вывода о наличии причинной взаимосвязи между воздействием и «откликом» или, в более привычных терминах, между независимой и зависи­мой переменными.

В главах, посвященных массовым опросам и статистическому анализу резуль­татов социологического исследования, обсуждаются возможности и ограничения неэкспериментальных, сугубо статистических методов анализа связи меж­ду переменными. В частности, речь идет о случаях ложной корреляции между переменными, а также о том, что в неэкспериментальных исследованиях часто невозможно однозначно упорядочить изучаемые переменные во времени и, сле­довательно, задать направление причинной связи². Основанная на эксперимен­те модель статистического вывода в значительной степени лишена этих недо­статков, хотя ее использование в социальных науках во многих случаях также сталкивается с существенными техническими, этическими и прочими ограни­чениями.
Определение и виды эксперимента.

Основные принципы экспериментирования

в социальных науках

Экспериментальный метод пришел в социальные науки из естественных наук, где он примерно с XVII века стал основным способом опытной проверки научных теорий¹. Самым популярным видом эксперимента в точных науках был и остается лабораторный эксперимент, получивший распространение также в науках о человеческом поведении.

Лабораторный, или истинный, эксперимент нацелен на проверку теоретичес­кой гипотезы и осуществляется в условиях максимального контроля над уров­нем воздействия независимой переменной и очищения (изоляции) этого воз­действия от посторонних влияний, оказываемых внешними, т. е. иррелевантными с точки зрения проверяемой гипотезы, переменными. Экспериментальный контроль и изоляция позволяют отвергнуть иные возможные объяснения на­блюдаемого эффекта — конкурентные гипотезы. Немаловажным условием обо­снованности, валидности результатов, получаемых в лабораторном эксперимен­те, является возможность достаточно надежного измерения зависимой переменной. В этом случае при бесконечном количестве испытаний результаты неизбежных случайных возмущений в зависимой переменной «погасят» друг друга и исследователь получит точную оценку интересующего его воздействия.

На практике описанные требования к истинному эксперименту могут быть пол­ностью воплощены лишь в бесконечном идеальном эксперименте, при прове­дении которого внешние, так называемые экзогенные переменные остаются неизменными, и изменяется лишь независимая переменная, что обеспечивает полную валидность выводов о изучаемом соотношении между независимой и зависимой переменными². Идеальный эксперимент — это эталон, относитель­но которого могут оцениваться и сопоставляться эксперименты реальные, од­нако буквальное выполнение всех его требований обычно невозможно или даже бессмысленно с точки зрения конкретной научной задачи, стоящей перед ис­следователем.

Дональд Кэмпбелл приводит в качестве примера эксперимент Николсона и Карлслайла, которые продемонстрировали явление гидролиза, всего лишь «взяв в мае 1880 г. образец воды в районе Сохо (образец очень частный, характерный для местных условий и данного периода) и опустив в него весьма специфичный кусок медной проволоки, по которой пропускался электрический ток...» Влиянием посторонних факторов (прежде всего примесей) на протекание гидролиза в данном эксперименте можно было пренебречь, так как целью было подтверждение теоретически предсказанной закономерности, а не измерение скорости гидролиза или изучение особенностей его протекания в различных средах³.

В социальных науках от лабораторного эксперимента принято отличать поле­вой эксперимент, проводимый в естественных условиях и в большинстве слу­чаев имеющий своей целью не столько проверку научной гипотезы о причинной связи между переменными, сколько оценку эффективности различных про­грамм или методов воздействия.

Для многих прикладных социологических исследований, ориентированных на разработку и оценку социальных программ, социальное экспериментирование столь же типично, сколь типичны лабораторные эксперименты для социальной психологии или социологии малых групп. Социальное экспериментирование позволяет ответить на самые разнообразные вопросы, относящиеся преимуще­ственно к сфере практической политики и администрирования — например, как влияет отмена смертной казни на показатели преступности, растет ли посе­щаемость музеев при снижении цен на входные билеты, во всех ли случаях повышение размера вознаграждения ведет к росту производительности тру­да и т. п.

Например, в исследовании воздействия детского сериала «Улица Сезам» на культурное и интеллектуальное развитие американских дошкольников¹ полевой эксперимент охватил детей и родителей, проживавших в городах (Бостон, Дарэм, Феникс), а также в сельских районах Калифорнии и Филадельфии. В ходе эксперимента детей и их родителей побуждали к просмотру сериала (независимая переменная), фиксируя изменения в когнитивном развитии дошкольников с помощью тестов достижений и тестов общего развития (зависимые переменные). Двухлетний полевой экспери­мент позволил продемонстрировать заметный обучающий эффект, связан­ный с просмотром сериала, особенно очевидный в группе детей из небла­гополучных семей.

Полевой эксперимент — ведущий метод ориентированных на практику оценоч­ных исследований (evaluative research)². Однако далеко не всегда оценка эффек­тивности новой, компьютеризованной системы обучения или, скажем, нового танкового прицела происходит в реальных полевых условиях. Иногда исследо­ватели проводят эксперимент в условиях, имитирующих реальность или даже представляющих некоторые особенности реальной ситуации — обучения, вож­дения танка и т. п. — в преувеличенном, «очищенном» виде. Р. Готтсданкер пред­ложил различать два типа полевых экспериментов — эксперименты, дублирую­щие реальный мир (т. е. уже описанные «натурные» эксперименты), и экспери­менты, улучшающие реальный мир³. Эксперименты, улучшающие реальный мир, прежде всего позволяют повысить валидность и надежность данных. Так, данные «натурного» эксперимента по эффективности нового метода обучения вождению автомобиля будут подвержены влиянию множества трудноконтро­лируемых различий в условиях видимости, ландшафте, состоянии дорог и ис­пользуемых автомобилей, тогда как данные тренажерных испытаний будут мень­ше подвержены такого рода смещениям. Кроме того, надежность эксперимента в «улучшенных» условиях также повысится за счет возможности контролиро­вать частоту «встречного движения» на экране тренажера, соблюдать четкий временной режим, исключающий утомление оператора, и т. д.

Для того чтобы понять, чем руководствуются социологи, осуществляя выбор одного из перечисленных видов эксперимента и конкретного плана построения экспериментального исследования, нам следует сначала рассмотреть ключевые понятия и принципы, лежащие в основе современного подхода к социальному экспериментированию.

Суммируя вышеизложенное, можно сказать, что в лабораторном эксперименте обоснованность выводов экспериментального исследования, т.е. их валидность и надежность, обеспечиваются благодаря трем принципам планирования экс­перимента: 1) контролю над уровнем независимой переменной, 2) изоляции основного эффекта (т. е. собственно воздействия независимой переменной на зависимую переменную) от влияния посторонних, смешивающих факторов, а также 3) многократному воспроизведению полученных результатов, которое позволяет нивелировать случайные изменения результата⁴ отдельных испыта­ний, связанные с несистематическими колебаниями фона, случайными ошиб­ками, усталостью и т. п. При этом первые два принципа планирования лабора­торного эксперимента позволяют обеспечить валидность как соответствие эксперимента его цели, измерение именно того эффекта, который предполага­лось измерить. Идеальный, т. е. совершенно валидный эксперимент, фиксирует лишь то отношение между переменными, которое и планирует изучить экспе­риментатор, и «отсекает» любые другие источники систематической вариации результатов. Валидность эксперимента, следовательно, определяет достовер­ность выводов о наличии либо отсутствии предполагаемой причинной связи и о подтверждении либо неподтверждении проверяемой в эксперименте теорети­ческой гипотезы (рис. 1). Третий принцип обеспечивает надежность результа­тов — защиту от случайной ошибки, являющуюся, как говорилось выше, необ­ходимым условием валидности.

Однако большая часть экспериментов в социальных науках (как, впрочем, и в ряде инженерных дисциплин или агробиологии) происходит в условиях, когда перечисленные принципы не могут быть реализованы полностью. Возникаю­щие здесь ограничения имеют технический, а иногда — скорее принципиаль­ный характер. Если, например, в социологическом эксперименте независимы­ми переменными служат раса или социальное происхождение, то мы даже тех­нически — не говоря уже о соображениях морали — не можем осуществлять полный контроль над этими переменными, т. е. совершенно произвольно опре­делять их значение для каждого отдельного случая (субъекта). И даже если бы эту трудность можно было бы каким-то образом преодолеть на время проведе­ния испытаний, нам было бы трудно изолировать интересующий нас основной эффект от влияния сопутствующих, «закоррелированных» с независимой пере­менной факторов, — связанного с расой или происхождением специфического социального опыта, соответствующих социальных навыков и т. п. (Со схожими трудностями сталкивается и агробиолог, оценивающий урожайность нового сорта пшеницы и пытающийся отделить главный фактор от прочих, также вли­яющих на урожайность: различий в освещенности опытных участков, в соста­ве почвы и т. п.).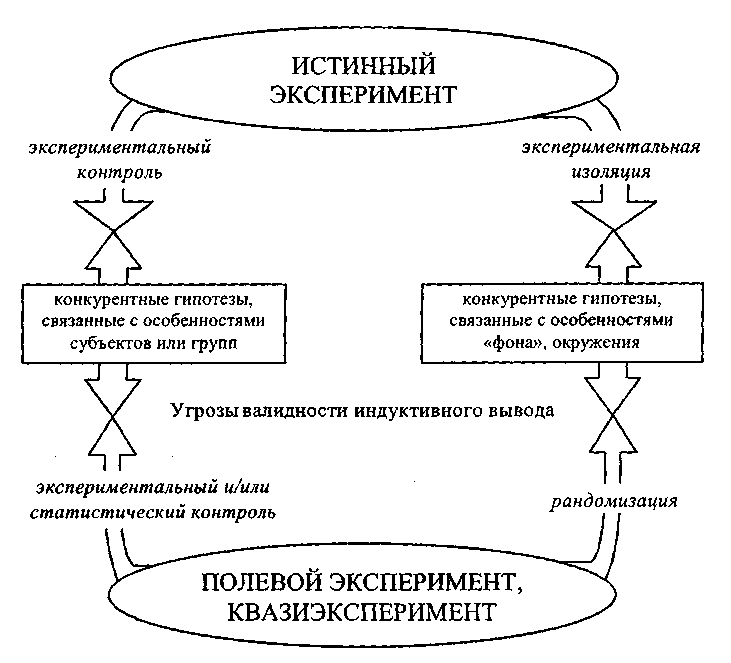

Рис. 1. Типы экспериментов
Знаменитый английский статистик Р. Фишер первым обосновал возможность применения несколько иного подхода к планированию полевых экспериментов, лабораторных экспериментов с неполным контролем, а также квазиэкспе­риментов (о последних речь пойдет позднее). Этот подход основан на целе­направленном использовании законов случая и теории вероятности. Он требует введения в планирование эксперимента принципа рандомизации.

Рандомизация — это стратегия случайного распределения субъектов по раз­личным условиям (режимам) эксперимента и экспериментальным группам.

Воспользуемся в качестве иллюстрации тем же простым примером психофизи­ческого опыта, которым пользуется сам Фишер при обсуждении роли принципа рандомизации в планировании эксперимента¹.

Представим себе, что некая леди взялась угадать, в какие четыре из восьми чашек чая с молоком сначала налили молоко, а в какие — чай. Эксперименталь­ная гипотеза состоит, таким образом, в том, что испытуемая обладает описан­ной способностью различения. Если воспользоваться простейшей формулой из комбинаторики, то общее число способов выбрать четыре чашки из восьми равно числу размещений А:


Иными словами, если бы испытуемая не обладала способностью отличать «молочно-чайные» чашки от «чайно-молочных» и прибегла к случайному угадыва­нию, то вероятность правильно определить 4 чашки составила бы ¹/₇₀ (из 70 существующих различных способов выбрать 4 чашки из 8 лишь один является правильным). Говоря точнее, при достаточно длинной серии испытаний частота правильных ответов приближалась бы к ¹/₇₀. Если же частота правильных ответов существенно, с точки зрения избранного статистического критерия, превышает частоту случайного угадывания, то мы вправе сделать вывод о том, что интересующая нас специальная способность действительно существует.

Однако описанная схема испытания явно не соответствует тем требованиям, которые предъявляются к уровню контроля над переменными и изоляции основного эффекта в лабораторном эксперименте. Возможные угрозы валидности наших статистических выводов носят довольно очевидный характер. Во-первых, мы не обладаем никакими средствами прямого измерения зависимой переменной — способности вкусового различения. Правильные угадывания — это лишь косвенные индикаторы такой способности и могут отражать влияние «посторонних» переменных, даже превосходящее основной эффект. Если, на­пример, во все чашки, в которые сначала было налито молоко, был добавлен сахар, ясно, что все они будут безошибочно опознаны. Статистические выводы о значимости окажутся, таким образом, невалидными, т. е. не имеющими отно­шения к нашей экспериментальной гипотезе (хотя и подтверждающими конкурентную гипотезу о способности распознавать сладкий вкус). Систематическое постороннее влияние, составляющее угрозу валидности статистического выво­да, может носить и другой характер: «молочные» и «чайные» чашки могут от­личаться друг от друга толщиной, температурой, цветом. Чтобы устранить пе­речисленные угрозы валидности и нивелировать возникающие систематичес­кие смещения, экспериментатор должен использовать принцип рандомизации, т. е. обеспечить случайный порядок предъявления стимулов-чашек и их оценки, определяемый, например, с помощью таблицы случайных чисел или жре­бия. В идеале и отбор испытуемых для каждой серии опытов, и распределение уровней независимой переменной между чашками («молоко-чай» или «чай-молоко») должны основываться на законах случая.

При планировании конкретного экспериментального исследования описанные принципы находят воплощение при разработке плана, или схемы, эксперимен­та, определяющего порядок предъявления испытуемым (или их группам) раз­личных уровней (условий) независимой переменной для адекватной проверки экспериментальной гипотезы².

Основные экспериментальные планы с контрольной

группой и рандомизацией

В социологии, психологии и других поведенческих науках особую роль играет использование принципа рандомизации при распределении испытуемых по груп­пам. В эксперименте с неполным контролем или в полевом эксперименте, про­исходящем в естественных условиях (т. е. в условиях школьного класса, про­мышленной организации, городского района и т. д.) часто нужно доказать не только наличие ожидаемого эффекта в результате некоторого воздействия Х, но и отсутствие того же эффекта в тех случаях, когда воздействия не было. Например, исследователь, изучающий воздействие просмотра антивоенных фильмов на изменения установок студентов, случайным образом отбирает из некоторой совокупности студентов экспериментальную группу, которой будет показан антивоенный фильм, а также контрольную группу, которой он продемонстрирует нейтральный фильм, никак не связанный с изучаемыми установ­ками. План этого простейшего рандомизированного эксперимента с предва­рительным и итоговым тестированием и контрольной группой (RT₁-₂C) будет выглядеть таким образом:

R О₁ Х О₂

R О₃ О₄
где R — процедура рандомизации (случайного распределения по группам), О_1,2 — уровни установок в экспериментальной группе до и после просмотра фильма X, O₃,₄ — уровни установок в контрольной группе, не смотревшей фильма. Ис­пользование контрольной группы позволяет устранить некоторые важнейшие угрозы валидности эксперимента. Во-первых, если бы исследователь отказался от использования контрольной группы и ограничился тестированием, т. е. из­мерением установок «до-после» просмотра, то обнаруженные изменения в уров­не установок можно было бы приписать влиянию на испытуемых самого по себе факта участия в эксперименте. Испытуемые, возможно, осознавали, что они отобраны для важного исследования и стремились некоторым образом со­ответствовать своей роли и оправдать некие гипотетические «ожидания» экспериментатора. Описанная угроза валидности широко известна и для нее суще­ствует несколько обозначений. В психологическом тестировании и эксперимен­тальной психологии это называют «эффектом морской свинки» или «мотивом экспертизы». Иногда применяют термин, возникший в медицине, где при кли­нических испытаниях новых фармакологических средств и методов лечения часто наблюдают «эффект плацебо», т. е. заметное улучшение статуса у многих участников контрольной группы, в которой вместо реального воздействия ис­пользовались индифферентные средства и нейтральные врачебные манипуля­ции. В социологии самое популярное обозначение систематического смещения, возникающего из-за реакции испытуемых на ситуацию эксперимента — это «хоуторнский эффект».

В так называемых хоуторнских экспериментах (по названию промышлен­ного предприятия в Чикаго) исследовались организационные и социаль­но-психологические факторы, влияющие на производительность труда. Исследователи обнаружили, что эффект роста производительности труда в бригадах сохранялся даже при отсутствии собственно экспериментального воздействия. Предположительной причиной этого явления был рост группового самосознания у участников эксперимента¹.

«Хоуторнский эффект»² — это угроза валидности, связанная с особенностями экспериментальной группы.

Еще одна угроза валидности выводов, которую позволяет преодолеть описыва­емый план эксперимента, также связана с особенностями групп, а именно — с процессом отбора для участия в эксперименте. Если бы мы отказались от предварительного тестирования и случайного распределения испытуемых по экспериментальной и контрольной группам, мы совершили бы методическую ошибку, весьма характерную для любых экспериментов с добровольцами. Очень часто исследователи отбирают испытуемых для участия в специальной программе обучения или в новаторском организационном проекте, основываясь на изъявленном ими желании, а затем сравнивают результаты, показанные участниками оцениваемой программы, с результатами какой-либо другой доступной группы (или даже случайной выборки из соответствующей генеральной сово­купности), не участвовавшей в такого рода программе. Однако такое сравнение некорректно: само по себе желание участвовать в эксперименте часто свидетельствует о изначально более высокой мотивации, осведомленности или ин­теллекте. Эти факторы сами по себе, или взаимодействуя с главной независи­мой переменной Х, могут объяснить значимые различия в результатах, показан­ных экспериментальной группой. В только что описанном примере сравнение группы добровольцев, пожелавших посмотреть антивоенный фильм, с прочи­ми студентами, может вести к завышенной оценке воздействия просмотра, если добровольцы изначально проявляют больший интерес к политическим пробле­мам. Лишь случайное распределение добровольцев по контрольной и экспери­ментальной группам при соблюдении «непрозрачности» такого распределения для всех испытуемых (участники обеих групп должны считать, что они подвергаются некоторому экспериментальному воздействию) позволяет судить о роли независимой переменной Xв возникновении межгрупповых различий¹.

Вышеописанные угрозы валидности связаны преимущественно с особенностя­ми групп, проявляющимися на стадии отбора или в ходе эксперимента. Однако рандомизация позволяет справиться и с некоторыми угрозами валидности, ис­ходящими от переменных внешнего окружения, фона. К фоновым относятся, в частности, «возможные влияния времени года или событий, возникающих на институциональном уровне», а также факторы естественного развития — «все те биологические или психологические процессы, которые независимо от кон­кретных внешних событий систематически изменяются с течением времени»². Испытуемые взрослеют, обучаются, устают, улучшают свои результаты при повторных тестированиях и т. п., что может сказываться на их результатах. Од­нако если такие посторонние влияния не оказывают избирательного воздей­ствия только на членов экспериментальной группы, они будут вносить вклад лишь в случайную ошибку, а не в систематическое смещение. Иными словами, они будут с равной вероятностью распределены между случайным образом ото­бранными участниками контрольной и экспериментальной групп. План типа RT₁-₂C позволяет обеспечить случайный и равновероятный характер внешних, фоновых воздействий на контрольную и экспериментальную группу. Более того, он позволяет «вычесть» величину фонового влияния и оценить чистый основ­ной эффект: если внешнее влияние все же имело место, оно в равной степени подействовало на показатели и экспериментальной, и контрольной групп; следовательно, разность между средними значениями первого и второго замеров уровня зависимой переменной в контрольной группе (О₄  О₃) нужно вычесть из аналогичной разности значений зависимой переменной, зафиксированной в экспериментальной группе (О₂O₁), т. е.:
Х    О₂O₁   О₄  О₃
при этом предварительное и послеэкспериментальное тестирование в экспери­ментальной и контрольной группах должны проводиться практически одновре­менно.

Систематическая угроза валидности, связанная с фоновыми факторами, может все же возникнуть и при использовании рандомизации и контрольной группы. Это происходит тогда, когда фоновые факторы взаимодействуют с независи­мой переменной (или некоторыми ее уровнями). Природу такого взаимодей­ствия легко понять на примере исследования, в котором изучается влияние тре­вожности, возникающей в ситуации неопределенности, на успешность реше­ния сложных задач. В такого рода экспериментах для создания ситуации неопределенности и повышения реактивной тревожности (независимые пере­менные) часто используют неясные инструкции, косвенные негативные оцен­ки действий испытуемого, высказываемые лицами, проводящими эксперимент (типа «Ну-ну, посмотрим, как Вы сможете это использовать»), а также предварительные серии, где испытуемому приходится решать заведомо неразреши­мые задачи. Разумеется, всем этим воздействиям (X) подвергаются лишь члены экспериментальной группы. Если испытуемые — это студенты, которым в силу случайного стечения обстоятельств через неделю предстоит сдавать экзамены, или сотрудники подразделения фирмы, ожидающие скорой переаттестации, то эти факторы «фона» будут взаимодействовать с независимыми переменными, не только суммируясь с ними, но и усиливая их эффект. Негативные подкрепле­ния, получаемые в ходе эксперимента, будут восприниматься значительно ост­рее накануне экзаменационной сессии или переаттестации, а связанная с этими событиями фоновая тревожность и неопределенность будет взаимодействовать с тревожностью и неопределенностью, создаваемыми преднамеренно.

Оценить чистый эффект взаимодействия с помощью сравнения с результатами контрольной группы вышеописанным способом в данном случае невозможно, так как взаимодействие фоновых смещений с основным эффектом происходит лишь там, где имеет место экспериментальное воздействие X. В контрольной группе приближающееся неприятное событие также может повлиять на резуль­таты итогового замера или даже обоих замеров, но оно не будет взаимодейство­вать, «перемножаться» с воздействием независимой переменной (такое взаимо­действие можно описать в более точных терминах, однако это требует введения некоторых статистических понятий). Для оценки величины взаимодействия фоновых смешивающих переменных с основным эф­фектом нужны более сложные экспериментальные планы. Некоторые из них будут обсуждаться ниже.

Иногда имеет смысл воспользоваться упрощенным вариантом описанного пла­на с рандомизацией и контрольной группой, а именно планом с рандомизаци­ей без предварительного тестирования (RTC), который схематически выгля­дит следующим образом:

R Х О₁

R О₂
Привлекательность этого плана заключается прежде всего в его экономичнос­ти. Если при распределении испытуемых между группами и уровнями воздействия использовалась истинная вероятностная процедура¹, то проведение пред­варительного тестирования — как в плане КТ_1-2С — лишь увеличивает стоимость эксперимента, не оказывая существенного влияния на качество получаемых данных. По сути, правильно осуществленная рандомизация (R) — это наилуч­шая гарантия отсутствия изначального смещения между группами (т. е. равен­ства исходных среднегрупповых значений зависимой переменной О в конт­рольной и экспериментальной группах). Кроме того, в широкомасштабных социологических исследованиях, а также в прикладных исследованиях в области педагогики и социальной работы, проведение и предварительных, и повтор­ных измерений зависимой переменной (политических установок, криминаль­ного поведения и т. п.) часто неосуществимо либо ведет к возникновению реак­ции на саму процедуру тестирования. Если, к примеру, мы изучаем влияние участия в предвыборной групповой дискуссии на последующую поддержку политических партий, то предварительное измерение политических установок может повлиять на активность опрошенных в ходе самой дискуссии и их пос­ледующие установки.

Можно заключить, что план RTC предпочтителен всегда, когда нежелательно повторное предъявление весьма специфичных по содержанию и схожих по форме тестов, вопросов, измерительных процедур. Иными словами, этот план заслуживает широкого применения в социологических и оценочных исследо­ваниях. Кроме того, он является самым приемлемым средством проведения так называемых методических экспериментов, в которых оценивается эффектив­ность различных видов опроса, способов заполнения и форматов анкет и т. п. (примером такого методического эксперимента является описанное в главе «Массовые опросы» исследование Бредберна и Судмана, в котором эффектив­ность метода «случайного ответа» сравнивалась с эффективностью использо­вания данных административной статистики). План RTC использовался, в час­тности, в одном из практически ориентированных социальных экспериментов по совершенствованию системы правоохранительных и пенитенциарных уч­реждений, проводившихся в США в 196070-е гг.

В 1961 г. Федеральное бюро пенитенциарных учреждений США начало трехлетний эксперимент, целью которого было изучить воздействие под­держивающего консультирования и специальных реабилитационных про­грамм на поведение мальчиков-подростков, находящихся в исправительных учреждениях. Местом проведения эксперимента стала специальная школа-колония для несовершеннолетних правонарушителей.

При проведении рандомизации мальчиков случайным образом распреде­ляли между отрядами, где проводился эксперимент, и отрядами, служившими контрольными (каждый отряд жил в отдельно расположенном корпусе). В экспериментальных отрядах было увеличено количество воспитателей, проводились специальные индивидуальные и групповые консуль­тации, использовалась система вознаграждений за хорошее поведение. В контрольных группах применялись обычные методы воспитания и обу­чения, а также традиционные наказания за нарушение внутреннего распорядка. Результаты эксперимента показали, что мальчики из экспериментальных групп раньше покидали спецшколу, лучше успевали в учебе, вели себя адаптивнее. Не было обнаружено значимых различий в показателях рецидивной преступности для подростков из экспериментальных и конт­рольных групп, освобожденных из школы-колонии, однако ребята из экс­периментальных групп значительно отличались от ребят из контрольных групп по показателю тяжести вновь совершенных преступлений (первые, в случае рецидива, совершали менее тяжкие преступления). По результатам эксперимента было принято решение о внедрении эксперименталь­ной коррекционной программы во всех подразделениях школы¹.

Еще один популярный план с рандомизацией и контрольной группой — это план Соломона². План Соломона — это расширенный вариант плана RT₁-₂C, позво­ляющий проконтролировать и оценить эффекты естественного развития и фона, а также определить взаимодействие эффекта тестирования с основ­ным воздействием X. Здесь наряду с экспериментальной и контрольной груп­пами с предварительным тестированием используются экспериментальная и контрольная группы без предварительного тестирования (как в плане RTC). Схематически это выглядит следующим образом:

R O₁X О₂

R О₃ О₄

RX О₅

R О₆
Очевидно, что если главный эффект X реален, то даже при наличии существен­ного эффекта тестирования («хоуторнского эффекта») будут выполняться четы­ре неравенства: O₂>O₁; О₂>О₄; О₅>О₆; О₅>О₃. Оценкой сравнительной вели­чины эффекта предварительного тестирования (без взаимодействия с X) может служить величина разности О₆О₃. Сравнение О₆с О₁и О₃ позволяет оценить влияние фоновых факторов и факторов естественного развития³.

До сих пор мы обсуждали содержательные аспекты проверки эксперименталь­ной гипотезы о наличии главного эффекта Xс помощью различных планов эк­сперимента, а также преимущества разных планов для обеспечения разных ас­пектов валидности. Очевидно, однако, что в каждом конкретном эксперименте величина главного эффекта, т. е. наблюдаемого различия результатов экспери­ментальной и контрольной группы, будет варьировать не только под воздей­ствием независимой переменной, но и просто в результате действия различных случайных возмущений. Конечно, если бы наш эксперимент был идеален и аб­солютно надежен (см. выше), то при каком угодно числе повторений мы бы всегда получали одну и ту же истинную оценку величины воздействия (при отсутствии или контроле смешивающего влияния дополнительных переменных). Однако реальные эксперименты — особенно, как уже говорилось, эксперимен­ты в социальных науках — не бывают и не могут быть идеальными и безупреч­но надежными. Следовательно, перед исследователем всегда стоит задача статистической оценки значимости полученных результатов.

Вероятностным «воплощением» содержательной экспериментальной гипоте­зы является статистическая гипотеза. Принятие или непринятие статисти­ческой гипотезы — необходимое, но недостаточное условие принятия или от­вержения содержательной гипотезы, проверяемой в эксперименте. Проверяе­мая в конкретном эксперименте статистическая гипотеза всегда формулируется как гипотеза о том, что при бесконечном количестве повторений этого экспери­мента среднее различие между экспериментальной и контрольной группами (или между воздействием разных уровней независимой переменной) равнялось бы нулю. Такую статистическую гипотезу, фактически сводящуюся к утверж­дению о случайном характере наблюдаемых в реальном эксперименте разли­чий, называют нулевой гипотезой, или нуль-гипотезой (Н₀). Отвержение или неотвержение нуль-гипотезы позволяет говорить о том, что в данном экспери­менте содержательная гипотеза подтвердилась, либо подтвердилась противо­положная ей альтернативная гипотеза, либо не было получено подтверждения ни одной из них.

Вспомним воображаемый эксперимент Фишера с чаем и молоком, описанный в начале главы. Мы отмечали, что при использовании тактики случайного угады­вания испытуемая смогла бы правильно определить последовательность напол­нения чашки примерно в 1 случае из 70. Следовательно, 2 «попадания» из 100 даже при очень большом количестве испытаний едва ли могут считаться значи­мым результатом. Куда достовернее выглядят 90 или даже 95 «попаданий» из 100 (оставшиеся «ошибки» можно отнести на счет действия случайных факто­ров). Чтобы определить уровень значимости и построить доверительный ин­тервал в этом случае достаточно метода, описанного в главе 8.

Вообще, критерии значимости и статистические методы, используемые при проверке статистической гипотезы для конкретного плана эксперимента, назы­вают статистическими моделями. Для планов с контрольной группой основ­ная статистическая модель — это использование t-критерия, о чем подробнее говорится чуть ниже. Для более сложных планов многомерных или факторных экспериментов, общий обзор которых дается в следующем разделе главы, веду­щие статистические модели — это дисперсионный анализ и использование F-критерия Фишера.

Итак, для того чтобы оценить статистическую значимость в элементарных ран­домизированных планах, описанных выше, нам необходимо проверить стати­стическую гипотезу о разности средних значений зависимой переменной в кон­трольной и экспериментальной группах. Конкретное значение разности сред­них значений зависимой переменной в экспериментальной и контрольной группе, обнаруженное в отдельном эксперименте (скажем, 4 балла по некото­рой «шкале пацифизма»), нужно соотнести с определенным интервалом, в ко­торый это значение «укладывается» с заданной (доверительной) вероятностью. Иными словами, нужно решить задачу интервального оценивания, подобную задаче оценки отдельного параметра совокупности в выборочном обследова­нии (эта задача описана в гл. 8). Разница в том, что проводя эксперимент, мы интересуемся не вероятными пределами, в которых лежит некая характеристи­ка выборки из реально существующей совокупности, а пределами, в которых лежит полученный нами в эксперименте результат относительно результата во­ображаемой бесконечной совокупности идентичных экспериментов. Нулевая гипотеза утверждает, что истинное значение различия средних равно нулю, ва­рьируя в каких-то пределах от эксперимента к эксперименту (т. е. . Если удается показать, что полученное в эксперименте зна­чение разности групповых средних не позволяет принять нулевую гипотезу, то делается вывод о подтверждении гипотезы, противоположной нулевой (т.е. — о статистической значимости различий между груп­пами — и, значит, о подтверждении экспериментальной гипотезы (или о под­тверждении гипотезы, противоположной экспериментальной, — если различие между экспериментальной и контрольной группой оказалось с обратным зна­ком). Заметьте, что нулевая гипотеза всегда формулируется как гипотеза о том, что истинное значение разности средних (или, скажем, величины взаимосвязи между двумя переменными) равно нулю, а полученные в эксперименте величи­ны отличаются от нуля исключительно из-за случайной ошибки выборки. Чем дальше от нуля — в ту или другую сторону — расположено наблюдаемое значе­ние, тем больше его статистическая значимость и меньше вероятность того, что оно явилось результатом ошибки выборки.

Для того чтобы сравнить полученное в эксперименте с контрольной и экспери­ментальной группами значение разности между средними с гипотетическим выборочным распределением этой величины для бесконечного числа испыта­ний (такие распределения имеются не только для разности средних, но и для средних величин, стандартных отклонений и т. д.), нужно выс­читать стандартную ошибку разности между средними¹. Формула для стандарт­ной ошибки разности между средними — S_Мэ-_Мk—немного отличается от фор­мулы стандартной ошибки средней S_M²⁰, приведенной в главе 8. Тем не менее она весьма проста: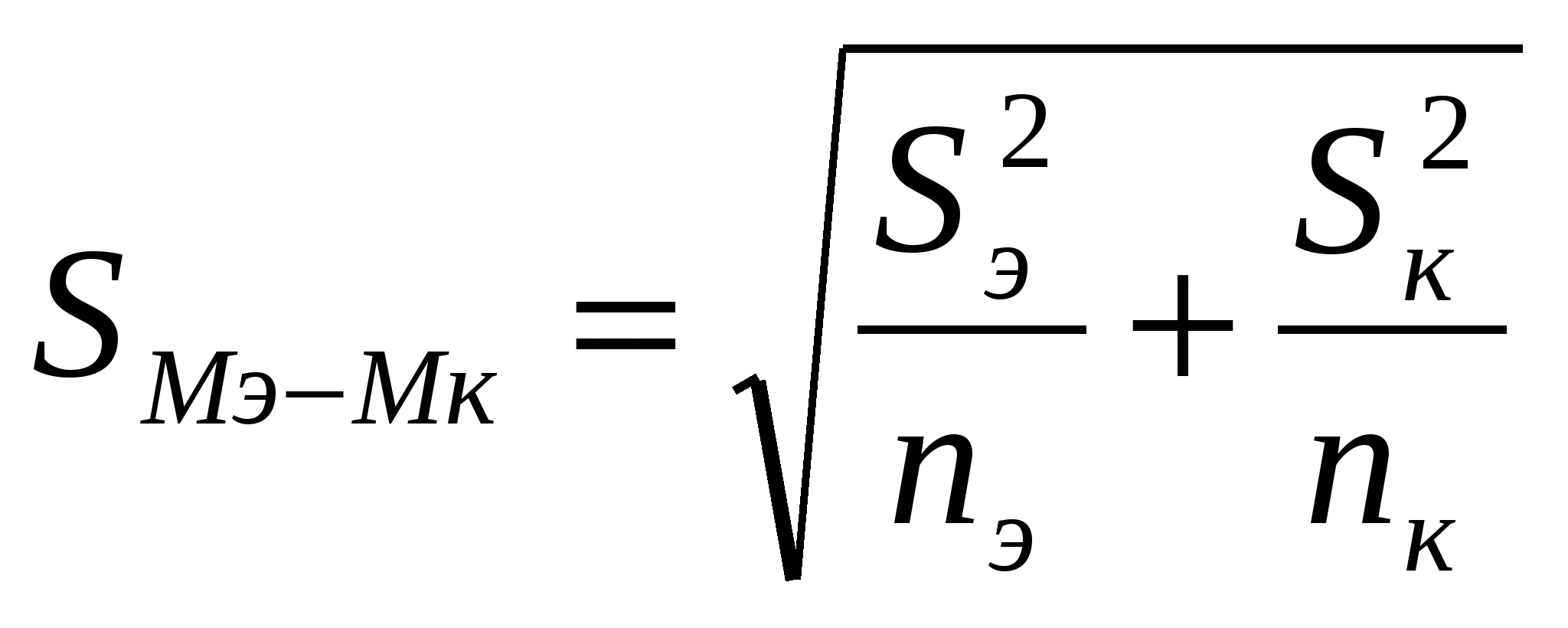

где S_э и S_K— величины стандартного отклонения, рассчитанные для экспери­ментальной и контрольной групп, n_э и п_k— число наблюдений (испытуемых) в экспериментальной и контрольной группах.

После этого нужно определить, на сколько единиц стандартной ошибки отсто­ит полученная разность средних от нуля, представляю-


щего собой — в согласии с нуль-гипотезой — среднее гипотетического распре­деления разностей средних, t-распределения. Для этого полученную в экспери­менте разность групповых средних нужно перевести в t-единицы (т. е. единицы стандартного отклонения для t-распределения). Для данной разности средних величину t можно высчитать по формуле:



Полученное значение t нужно сравнить с соответствующим значением из таблицы t-распределения для избранного уровня значимости (р = 0,05 или 0,01) и числа сте­пеней свободы, соответствующего количеству наблюдений в каждой группе (или подвыборке). Число степеней свободы — довольно сложное статистическое поня­тие, анализ которого выходит за пределы этого учебника (в самом общем виде оно обсуждается в гл. 7). На практике число степеней свободы можно рассматривать как величину, равную числу наблюдений (испытуемых, опрошенных, баллов и т. п.) минус число оцениваемых параметров. Для разности средних двух групп это со­ставит число наблюдений в экспериментальной группе минус один (n_э  1) плюс число наблюдений в контрольной группе минус один (п_k 1):

N_{ст.своб.} = (n_э  1) + (п_k 1)

Таблицы t-распределения можно найти в любом учебнике или справочнике по статистике (см. «Дополнительную литературу» к данной главе, а также к гл. 8). Здесь мы приводим лишь фрагмент такой таблицы.