ТММ РАСЧЁТЫ. Содержание курсовой работы
 Скачать 87.27 Kb. Скачать 87.27 Kb.
|
Определение ускорений точек звеньев механизма.Ускорение точки А, совершающей вращательное движение вокруг точки О, складывается из двух составляющих: 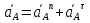 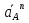 - вектор нормальной составляющей ускорения точки А, направленный к центру вращения и равный по модулю: - вектор нормальной составляющей ускорения точки А, направленный к центру вращения и равный по модулю: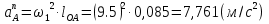 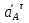 - вектор тангенциальной составляющей ускорения точки А, направленный перпендикулярно вектору нормальной составляющей. Поскольку в данном случае угловая скорость кривошипа задана постоянной, то угловое ускорение кривошипа - вектор тангенциальной составляющей ускорения точки А, направленный перпендикулярно вектору нормальной составляющей. Поскольку в данном случае угловая скорость кривошипа задана постоянной, то угловое ускорение кривошипа 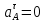 . .Определим масштабный коэффициент: 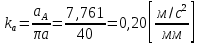 На основании теоремы сложения ускорений (вектор абсолютного ускорения точки равен сумме векторов ускорений в переносном движении, относительном и ускорения Кориолиса) можем записать: 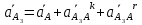 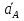 - вектор ускорения точки А кривошипа и кулисного камня (величина и направление его известны); - вектор ускорения точки А кривошипа и кулисного камня (величина и направление его известны);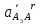 - вектор относительного ускорения точки - вектор относительного ускорения точки 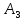 кулисы относительно точки А (у него известно только направление – вдоль кулисы АС); кулисы относительно точки А (у него известно только направление – вдоль кулисы АС);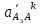 - вектор ускорения Кориолиса, по модулю равный: - вектор ускорения Кориолиса, по модулю равный: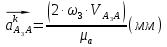 Кориолисово ускорение возникает в том случае, когда вектор относительной скорости поворачивается (т.е. переносное движение – вращательное). Направление его определяется поворотом вектора относительной скорости 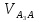 на на 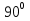 в направлении переносной угловой скорости в направлении переносной угловой скорости 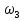 . .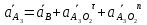 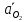 – вектор ускорения точки – вектор ускорения точки 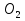 (переносное ускорение, равное нулю, так как точка (переносное ускорение, равное нулю, так как точка 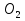 принадлежит ещё и стойке); принадлежит ещё и стойке);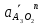 - нормальная составляющая вектора относительного ускорения точки - нормальная составляющая вектора относительного ускорения точки 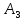 относительно точки относительно точки 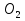 равная по модулю: равная по модулю: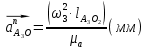 и направленная к центру вращения, т.е. от точки 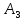 к точке О; к точке О;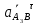 - тангенциальная составляющая вектора относительного ускорения точки - тангенциальная составляющая вектора относительного ускорения точки 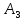 относительно точки B, для которого известно только направление, перпендикулярное нормальной составляющей (или кулисе О2A). относительно точки B, для которого известно только направление, перпендикулярное нормальной составляющей (или кулисе О2A).Найдём действительные значения ускорения 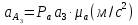 Угловые ускорения 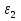 и и 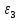 можно определить с помощью найденной в результате решения уравнений тангенциальной составляющей ускорения вращательного движения: можно определить с помощью найденной в результате решения уравнений тангенциальной составляющей ускорения вращательного движения: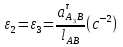 Ускорение точки B найдём по принципу подобия в плане ускорений: 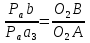 ; ; 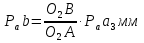 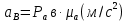 Определим ускорение точки С, для чего составим уравнение: 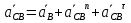 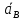 – вектор ускорения, величина и направление которого известны; – вектор ускорения, величина и направление которого известны;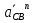 - вектор нормальной составляющей относительного (вращательного) ускорения точки C относительно точки B, по модулю равный: - вектор нормальной составляющей относительного (вращательного) ускорения точки C относительно точки B, по модулю равный: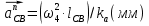 и направленный вдоль звена ВС к точке В. 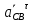 - вектор тангенциальной составляющей, у которого известно только направление – перпендикулярно звену CB. Также нам известно направление ускорения точки C – горизонтальное . - вектор тангенциальной составляющей, у которого известно только направление – перпендикулярно звену CB. Также нам известно направление ускорения точки C – горизонтальное .Найдём действительные значения ускорений: 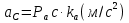 Вектор ускорения точки S4 найдем соединив полюс ускорения с центром отрезка BC. 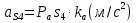 Угловое ускорение звена СВ определяется: 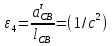 Таблица №2 Результаты построения и расчетов планов ускорений.
|
