ТММ РАСЧЁТЫ. Содержание курсовой работы
 Скачать 87.27 Kb. Скачать 87.27 Kb.
|
Построение кинематических диаграммДиаграмма перемещения. Для построения диаграммы перемещения точки С ползуна 5 по оси абсцисс откладывается отрезок b=150 мм, изображающий период Т одного оборота кривошипа, и делим его на 12 равных частей. От точек 1, 2, …, 11 диаграммы s(t) откладываются ординаты С0-С1, С0-С2, С0-С11, проходимые точкой С от начала отсчета. Строится диаграмма изменения скорости точки С V() путем графического дифференцирования кривой S(). Выбирается отрезок H1=22 мм. Проводим касательную к S() на соответствующих участках от 0 до 11. Точки их пересечения с осью ординат и дадут совокупность точек графика VС (). Строится кривая. Аналогичным методом графического дифференцирования, но уже графика VС (), строится график aС (). Выбирается отрезок H2 = 14 мм. Выбираем масштаб: 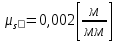 Масштаб угловой координаты 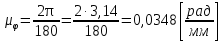 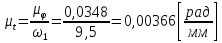 Построение диаграммы скоростей ведём методом графического дифференцирования, методом хорд. 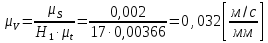 Построение диаграммы ускорений ведём методом графического дифференцирования, методом хорд. 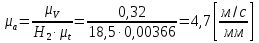 При построении планов скоростей руководствуются следующими правилами: — вершины векторов скоростей точек обозначают строчными буквами, теми же что и сами точки; — если вектор скорости точки равен нулю, то буквенные обозначения его вершины и начала совпадают, т.е. на плане тождественно равны; — кинематические уравнения состоят из левой и правой частей, разграниченных знаком равенства, построение каждой части начинают от полюса плана — р независимо друг от друга; — сложение векторов выполняют по правилу треугольника. Для определения направления угловой скорости звена нужно вектор относительной скорости какой-либо точки звена мысленно перенести из плана скоростей в саму эту точку, полюс на звене остановить, тогда направление относительной скорости точки укажет направление вращения звена вокруг его полюса. Построим диаграмму скорости точки С 5-го звена в зависимости от времени цикла: 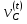 . Для этого графически продифференцируем график перемещения этой точки . Для этого графически продифференцируем график перемещения этой точки 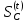 . Используем метод хорд. . Используем метод хорд.Под диаграммой 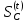 (приложение Г) подготовим координатное поле для будущего графика скорости. Проведем ось ординат (приложение Г) подготовим координатное поле для будущего графика скорости. Проведем ось ординат 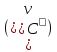 высотой порядка 200...300 мм. Ось абсцисс (t) изобразим так, чтобы она делила ось высотой порядка 200...300 мм. Ось абсцисс (t) изобразим так, чтобы она делила ось 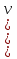 ) пополам. ) пополам.На оси времени отложим отрезок lt , такой же длины, как и на диаграмме 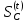 . Аналогично делим его на 12 равных частей, характеризующих равные временные отрезки, концы которых также обозначим 1, 2, 3,...14. . Аналогично делим его на 12 равных частей, характеризующих равные временные отрезки, концы которых также обозначим 1, 2, 3,...14.Зададимся конструктивно полюсным расстоянием Н (выберем его длину из рекомендуемого интервала 30...70 мм, например, Н =40 мм). Отложим расстояние Н на продолжении оси абсцисс (времени) влево от начала отсчета. Конец отрезка обозначим Р (полюс). От величины Н зависит общая высота графика 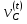 . При увеличении Н растет и высота диаграммы. Поэтому, если в результате построений диаграмма не помещается в отведенном пространстве листа (либо наоборот, окажется чрезмерно мала), необходимо изменить соответствующим образом величину Н и повторить построение. . При увеличении Н растет и высота диаграммы. Поэтому, если в результате построений диаграмма не помещается в отведенном пространстве листа (либо наоборот, окажется чрезмерно мала), необходимо изменить соответствующим образом величину Н и повторить построение.Кроме того, можно поступить наоборот: рассчитать полюсное расстояние Н (мм), предварительно задавшись (ориентировочно) общей высотой будущей диаграммы скорости — hv: 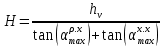 Здесь 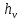 – общая высота диаграммы скорости, задаётся конструктивно в пределах 200…300 мм; – общая высота диаграммы скорости, задаётся конструктивно в пределах 200…300 мм;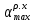 , , 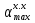 – наибольшие острые углы наклона хорд диаграммы – наибольшие острые углы наклона хорд диаграммы 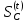 к оси абсцисс, измеряемые на восходящем её участке (рабочий ход) и нисходящем (холостой ход). к оси абсцисс, измеряемые на восходящем её участке (рабочий ход) и нисходящем (холостой ход).На диаграмме перемещения 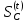 соединим точки 0, 1”, 2", 3"... 11", 12 прямыми отрезками (хордами). Получим ломаную линию, вписанную в диаграмму перемещения. соединим точки 0, 1”, 2", 3"... 11", 12 прямыми отрезками (хордами). Получим ломаную линию, вписанную в диаграмму перемещения.Если рассматривать диаграмму перемещения 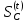 именно как ломаную линию, то в этом случае на каждом временном интервале: 0-1, 1-2, … 14 можно считать, что скорость точки С остается постоянной, и меняется ступенчато при переходе к следующему интервалу в моменты времени: 1,2,3...14. именно как ломаную линию, то в этом случае на каждом временном интервале: 0-1, 1-2, … 14 можно считать, что скорость точки С остается постоянной, и меняется ступенчато при переходе к следующему интервалу в моменты времени: 1,2,3...14.Из полюса Р проведем наклонные линии параллельно полученным хордам до пересечения с осью ординат ( 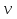 ). Точки пересечения их с осью ординат обозначим по порядку построения: 1", 2"', 3"... 11", 14". ). Точки пересечения их с осью ординат обозначим по порядку построения: 1", 2"', 3"... 11", 14".Отмеченные отрезки на оси ординат 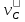 : (от начала отсчета до точек пересечения ее линиями параллельными хордам диаграммы : (от начала отсчета до точек пересечения ее линиями параллельными хордам диаграммы 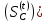 пропорциональны средним скоростям точки С на соответствующих интервалах ее движения. пропорциональны средним скоростям точки С на соответствующих интервалах ее движения.Проведем из точек 1", 2". 3"... 11", 14" горизонтальные прямые до середины соответствующих им интервалов времени движения: 0-1, 1-2...11-12. Отметим, таким образом, узловые точки будущей диаграммы скорости. Соединим полученные точки плавной кривой линией. Получим диаграмму скорости точки С выходного 5 звена в течение цикла работы механизма - 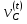 (приложение Г). (приложение Г).Определим масштабный коэффициент оси скорости построенной диаграммы. Он зависит от масштабных коэффициентов интегральной кривой: диаграммы перемещения точки С — 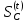 и выбранного предварительно полюсного расстояния Н: и выбранного предварительно полюсного расстояния Н: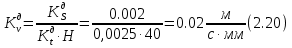 Нанесем на поле диаграммы координатную сетку с размером ячейки в 1 см. Подпишем деления осей времени t и скорости 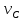 в соответствии с масштабными коэффициентами в соответствии с масштабными коэффициентами 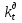 и и 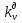 Пользуясь диаграммой, определим величину скорости точки С в рассматриваемых временных позициях:1, 2, 3...13. Для этого используем формулу 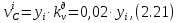 где 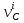 — величина скорости точки С в i-ой позиции, м/с; — величина скорости точки С в i-ой позиции, м/с;yi — измеряемая ордината диаграммы скорости, соответствующая ее i-ой позиции, мм. Результаты расчетов сведем в таблицу 3. Таблица 3 — Скорость точки С выходного звена, м/с.
2.5 Определим ускорений звеньев и их отдельных точек в одном из положений механизма Произведём расчёт ускорений в 4-м положении механизма.
Определим ускорение точки А. 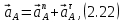 Где 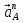 - нормальное ускорение точки А, направлено по радиусу траектории движения к центру её кривизны, т.е. от А к О1, численно определяется как - нормальное ускорение точки А, направлено по радиусу траектории движения к центру её кривизны, т.е. от А к О1, численно определяется как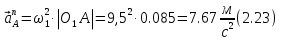 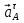 – касательное (тангенциальное) ускорение точки А, численно определяется как – касательное (тангенциальное) ускорение точки А, численно определяется как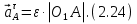 Здесь 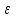 – угловое ускорение 1-го звена, равна нулю, поскольку, согласно условию, вращение этого звено – равномерное – угловое ускорение 1-го звена, равна нулю, поскольку, согласно условию, вращение этого звено – равномерное 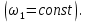 Тогда Тогда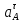 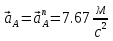 . .2.Рассмотрим группу Ассура из 2-3 звеньев (рисунок 2.9) Рисунок 2.9 – Анализ ускорений структурной группы Ассура из 2-3 звеньев По аналогии с определением скоростей составим и решим графически совместно два кинематических уравнения для ускорения точки А3 3-го звено. В одном случае, применим теорему сложения ускорений при сложном движении точки А3 (рисунок 2.9 а). Получим 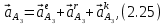 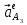 – переносное ускорение точки А3, равно ускорению совпадающей с ней точки шарнира А ( – переносное ускорение точки А3, равно ускорению совпадающей с ней точки шарнира А (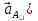 на несущем 2-м звене, найденному по формуле (2.22); на несущем 2-м звене, найденному по формуле (2.22);Где 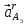 – ускорение точки А3 относительно шарнира А ( – ускорение точки А3 относительно шарнира А (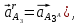 лотентировано вдоль линии АО2 неизвестно по величине; лотентировано вдоль линии АО2 неизвестно по величине;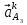 - Кориолисово ускорение точки А3. - Кориолисово ускорение точки А3.По определению Кориолисово ускорение находится как  Где 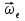 - вектор переносной угловой скорости, т.е. угловой скорости несущего для точки А3 2-го звена, - вектор переносной угловой скорости, т.е. угловой скорости несущего для точки А3 2-го звена, 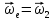 ; ;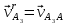 – вектор относительной скорости точки А3 в её движении, относительно второго звена, известен из формулы (2.12). – вектор относительной скорости точки А3 в её движении, относительно второго звена, известен из формулы (2.12).Величину Кориолисова ускорения найдём, раскрыв выражение (2.26) согласно правилу векторного произведения: 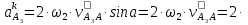 Последовательность действий аналогична построению плана скоростей. Будем изображать векторы в порядке их суммирования в уравнении (2.30) (рисунок 2.11) При построении планов ускорений руководствуются следующими правилами: — вершины векторов абсолютных ускорений точек обозначают строчными буквами, теми же что и сами точки; — вершины векторов нормальных относительных ускорений точек обозначают — ni, где индекс i соответствует номеру звена, которому принадлежит рассматриваемая точка; — вершины векторов Кориолисовых ускорений обозначают — ki , где индекс также соответствует номеру звена с рассматриваемой точкой; — если вектор ускорения точки равен нулю, то буквенные обозначения его вершины и начала совпадают, т.е. на плане тождественно равны; — кинематические уравнения состоят из левой и правой частей, разграниченных знаком равенства, построение каждой части начинают от полюса плана — π независимо друг от друга. |
