ТММ РАСЧЁТЫ. Содержание курсовой работы
 Скачать 87.27 Kb. Скачать 87.27 Kb.
|
2.3 Определение скоростей механизма.Известно, что задача определения скоростей (и ускорений) в плоских рычажных механизмах может считаться решенной, если для каждого из их звеньев будут найдены — скорость (и ускорение) одной какой-либо точки звена; — угловая скорость (и угловое ускорение) звена. Для рычажных механизмов 2-го класса эти цели обычно достигаются с помощью графоаналитического метода, состоящего в построении планов скоростей (и ускорений). План скоростей (ускорений) механизма — многоугольник из векторов, изображающих абсолютные и относительные скорости (ускорения) точек звеньев механизма в конкретном его положении. При построении плана скоростей механизма последовательно рассматриваются его структурные группы Ассура в порядке образования механизма. Предварительно рассматривается входное звено. Определяется аналитически скорость точки — элемента кинематической пары, соединяющей входное звено с ближайшей структурной группой Ассура. При анализе каждой структурной группы руководствуются следующими общими положениями.
1 — теорема сложения скоростей (и ускорений) при плоскопараллельном движении тела (звена); 2 — теорема сложения скоростей (и ускорений) при сложном движении точки.
Угловые скорости звеньев определяют аналитически, делением относительной скорости какой-либо точки звена при ее движении вокруг другой его точки (полюса) на расстояние между ними. Планы скоростей всех групп Ассура строятся из одного полюса — р и, в конечном итоге, составляют общий план скоростей механизма. Планы скоростей обладают тремя свойствами: 1 — абсолютные скорости точек изображаются векторами, исходящими из полюсов планов — р; 2 - относительные скорости точек изображаются векторами, соединяющими вершины векторов абсолютных скоростей;
Рассмотрим алгоритм построения планов скоростей и ускорений в общем виде. 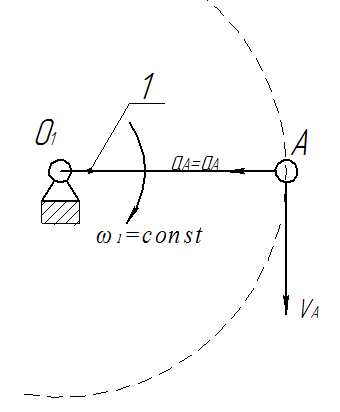 Скорость точки А: 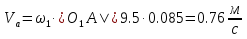 , где , где 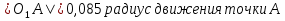 Принимаем длину отрезка (pva) изображающего ускорение точки А, равной 60 м/с2 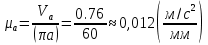 2. Рассмотрим группу Ассура из 2-3 звеньев (рисунок. 2.2) Выберем точку в средней кинематической паре (поступательной) — А3, расположенную на 3-м звене под шарниром А. Выразим ее абсолютную скорость, считая движение этой точки сложным (рисунок 2.2(а)). Оно состоит из переносного движения (вместе с несущим звеном 2) и относительного — вдоль направляющей звена 2. Применим теорему сложения скоростей при сложном движении точки А3 Получим уравнение: 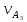 = = 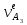 + +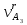 Скорости остальных точек механизма находим путем построения плана скоростей. Принимаем длину отрезка (pva) изображающего скорость va точки А, равной 40 мм. 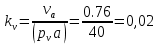 Составим векторные уравнения для получения абсолютной скорости точки А. 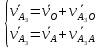 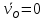 , , 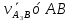 , , 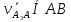 Величина скорости точки A3: 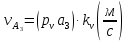 Скорость точки В определяем с помощью теоремы подобия: 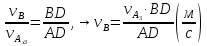 Векторные уравнения для нахождения скорости точки C имеют следующий вид: 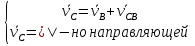 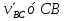 , ,Скорость точки C: 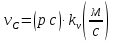 Скорость точки S4 найдем соединив середину отрезка bc с полюсом . 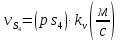 Определение угловых скоростей звеньев: 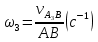 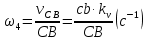 Таблица №1. Результаты построения и расчетов планов скоростей.
|
