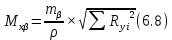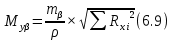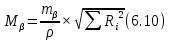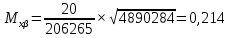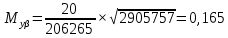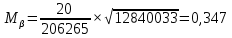Диплом по маркшейдерии. Спец часть (2)Бовтрук новое. Создание опорной подземной маркшейдерской сети на месторождение Юбилейное
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
6.2.3 Методика производства горизонтальных маркшейдерских съемок при создании опорных сетейУгловые измерения В полигонометрических ходах, прокладываемых по выработкам с углом наклона менее 30  , углы измеряются одним повторением или приемом. При измерении углов способом повторений разность между одинарным и окончательным (средним) значением угла допускается не более 45. При измерении углов способом приемов расхождение углов между полуприемами допускается не более 1[1]. , углы измеряются одним повторением или приемом. При измерении углов способом повторений разность между одинарным и окончательным (средним) значением угла допускается не более 45. При измерении углов способом приемов расхождение углов между полуприемами допускается не более 1[1].Линейные измерения Длины сторон в полигонометрических ходах измеряются стальными компарированными рулетками, светодальномерами и другими приборами, обеспечивающими необходимую точность. Стальные рулетки (ленты) компарируются с относительной погрешностью не более 1:15000. Линейные измерения выполняются при постоянном натяжении мерного прибора, равным натяжению при компарировании. Сила натяжения фиксируется динамометром. Температура воздуха учитывается в том случае, если изменение ее относительно температуры компарирования превышает 5о. Длины сторон полигонометрических ходов измеряются дважды - в прямом и обратном направлениях [1]. Перед использованием постоянных пунктов подземной маркшейдерской опорной сети измеряются контрольный угол и контрольная длина линии; разность между предыдущим значением угла и контрольным допускается не более 1; разность между предыдущим значением длины линии и контрольным допускается не более 1:3000 её длины. Основными факторами, влияющими на точность определения координат и дирекционных углов в опорной маркшейдерской сети, являются: ошибка ориентирования первой стороны, ошибки измерения длин линий и ошибки измерения горизонтальных углов теодолитных ходов. Обработка ведомости вычисления координат вершин полигонометрического хода Значение измеренных углов записывают в ведомость вычисления координат. Определение угловой невязки. Вычисляют сумму Σ βПР измеренных углов хода. Определяют теоретическую сумму углов 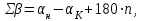 где n - число вершин хода. Находят угловую невязку fβ = Σ βПР - Σ βТ. Если невязка fβ не превышает допустимой величины, т.е. fβдоп = ± 1'n, то ее распределяют с обратным знаком поровну на все углы с округлением значений поправок до десятых долей минут. Сумма исправленных углов должна равняться теоретической. Вычисление дирекционных углов и румбов сторон хода. По исходному дирекционному углу αН и исправленным значениям углов β хода вычисляют дирекционные углы всех остальных сторон 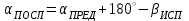 . .Вычисление приращений координат. Приращения координат вычисляют по формулам: 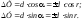 Затем складывают все вычисленные значения Х и У и находят практические (фактические) суммы приращений координат ∑ХПР и ∑УПР. Нахождение абсолютной и относительной линейных невязок хода; увязка приращений координат. Сначала вычисляют невязки fХ и fУ в приращениях координат по осям Х и У: fХ = ∑ХПР - ∑ХТ; fУ = ∑УПР - ∑УТ, где ∑ХТ, ∑УТ - теоретические суммы приращений координат. Абсолютную линейную невязку Р хода вычисляют по формуле 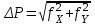 . .Относительная линейная невязка 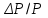 хода (Р - периметр хода) выражается простой дробью с единицей в числителе. хода (Р - периметр хода) выражается простой дробью с единицей в числителе. Если относительная невязка окажется меньше допустимой (1/2000), то невязки fХ и fУ распределяют с обратным знаком на соответствующие приращения и пропорционально длинам сторон, для чего вычисляют поправки 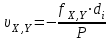 , , где di - длины линий (горизонтальных проложений). Суммы поправок по Х и У должны равняться невязкам fХ и fУ с противоположным знаком. Исправленные приращения записывают в графы 9 и 10; суммы исправленных приращений координат должны быть равны ∑ХТ , ∑УТ. Вычисление координат вершин хода. Координаты вершин хода получают путем последовательного алгебраического сложения координат предыдущих вершин хода с соответствующими исправленными приращениями: Х1 = Хтон + Хтон - 1; У1 = Утон + Утон - 1 Каталог координат всего полигонометрического хода представлен в приложении 6.2.4 Предрасчет погрешности положения наиболее удаленного пункта ОМС В практике маркшейдерских работ форму полигона определяют горные выработки. В нашем случае это висячий (свободные), опирающиеся на одну сторону полигон. Под твердой стороной понимают сторону, дирекционный угол которой определен. На ошибку координат такого полигона оказывают совместное влияние ошибки ориентирования (ошибка дирекционного угла исходной стороны), ошибки измерения углов сторон полигона. Для удобства дальнейших вычислений указанные на плане полигона значения, горизонтальных углов приведены с точностью до градуса, длин линий - до метра,представлены в таблице 6.2. Таблица 6.2 - Исходные данные полигона
Средняя погрешность положения конечного пункта (Мк) складывается из ошибок координат (Мx, My): 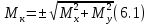 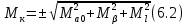 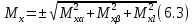 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| вершины углов | 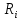 | 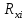 | 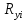 | 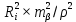 | 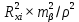 | 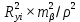 | |||
| м | |||||||||
| Т.порт | 1208,9 | 401 | 787,2 | 0,013738 | 0,001511606 | 0,005825 | |||
| 1 | 1170 | 435,7 | 770,9 | 0,012868 | 0,001784535 | 0,005587 | |||
| 2 | 1125 | 472,8 | 745 | 0,011897 | 0,002101381 | 0,005217 | |||
| 3 | 1098 | 488,9 | 723,7 | 0,011333 | 0,002246932 | 0,004923 | |||
| 4 | 1060 | 507,2 | 689,7 | 0,010562 | 0,00241829 | 0,004472 | |||
| 5 | 981,3 | 539,4 | 618,4 | 0,009052 | 0,002735091 | 0,003595 | |||
| 6 | 947 | 524,3 | 587,7 | 0,00843 | 0,002584101 | 0,003247 | |||
| 7 | 884,2 | 488,4 | 536 | 0,007349 | 0,002242338 | 0,002701 | |||
| 8 | 840,2 | 463,9 | 499,5 | 0,006636 | 0,002023013 | 0,002345 | |||
| 9 | 793,2 | 435,3 | 462,2 | 0,005914 | 0,001781259 | 0,002008 | |||
| 10 | 751 | 409,3 | 428,5 | 0,005302 | 0,001574829 | 0,001726 | |||
| 11 | 681,3 | 366 | 374,4 | 0,004363 | 0,00125925 | 0,001318 | |||
| 12 | 597,8 | 314,4 | 308,7 | 0,003359 | 0,000929212 | 0,000896 | |||
| 13 | 520,5 | 266,8 | 247,8 | 0,002547 | 0,000669147 | 0,000577 | |||
| 14 | 478,4 | 241 | 214,5 | 0,002151 | 0,000545989 | 0,000433 | |||
| 15 | 406,9 | 196,9 | 157,1 | 0,001556 | 0,000364453 | 0,000232 | |||
| 16 | 335,9 | 153,2 | 102,3 | 0,001061 | 0,000220631 | 9,84E-05 | |||
| 17 | 277,8 | 114,1 | 59,3 | 0,000725 | 0,000122383 | 3,31E-05 | |||
| 18 | 266 | 103,7 | 53,7 | 0,000665 | 0,00010109 | 2,71E-05 | |||
| 19 | 198,3 | 47 | 90,5 | 0,00037 | 2,07657E-05 | 7,7E-05 | |||
| 20 | 141,7 | 0,7 | 120,9 | 0,000189 | 4,60623E-09 | 0,000137 | |||
| 21 | 105,7 | 27,5 | 96,8 | 0,000105 | 7,10911E-06 | 8,81E-05 | |||
| 22 | 142,3 | 51,4 | 124,7 | 0,00019 | 2,48357E-05 | 0,000146 | |||
| 23 | 173,5 | 70,8 | 149,2 | 0,000283 | 4,71212E-05 | 0,000209 | |||
| 24 | 68,4 | 3,7 | 68,2 | 4,4E-05 | 1,28693E-07 | 4,37E-05 | |||
| 25 | 30,7 | 0,2 | 30,7 | 8,86E-06 | 3,76019E-10 | 8,86E-06 | |||
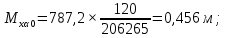
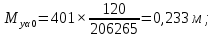
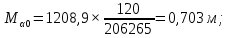
2. Средние погрешности координат точки хода, обусловленные погрешностью измерения горизонтальных углов
 ,
,  и ошибку положения конечного пункта
и ошибку положения конечного пункта 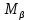 рассчитываем по следующим формулам:
рассчитываем по следующим формулам:где
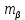 - средняя квадратическая ошибка горизонтального угла.
- средняя квадратическая ошибка горизонтального угла. Величина
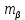 принимается в соответствии с требованиями маркшейдерской инструкции для соответствующего разряда сети. В нашем случае
принимается в соответствии с требованиями маркшейдерской инструкции для соответствующего разряда сети. В нашем случае 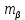 = 20.
= 20.3. Средние погрешности координат точки хода, обусловленные погрешностью измерения длин линий
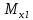 ,
, 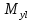 и положения конечного пункта
и положения конечного пункта 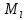 .
. Измерение длин сторон полигонометрического хода сопровождается случайными и систематическими погрешностями, каждые из которых соответственно будут оказывать влияние на погрешности.
Ошибки координат и линейную ошибку положения конечной точки в зависимости от ошибок измерения длин линий определяют по формулам:
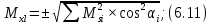
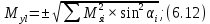
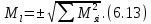
где
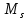 – средняя ошибка измерения длины.
– средняя ошибка измерения длины.Результаты вычисления погрешностей представлены в таблице 6.4.
Таблица 6.4 - Вычисление ошибки координат конечного пункта полигона в зависимости от ошибок измерения длин сторон
| стороны полигона | S | 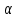 | 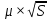 | 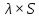 | 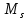 | 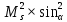 | 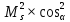 | 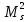 | ||
| 1 | - | 1 | 36 | 118 | 0,189737 | 1,8 | 1,9897 | 3,0865 | 0,8726 | 3,9591 |
| 2 | - | 1 | 45 | 193 | 0,212132 | 2,25 | 2,4621 | 0,3068 | 5,7553 | 6,0621 |
| 3 | - | 2 | 27 | 198 | 0,164317 | 1,35 | 1,5143 | 0,2190 | 2,0742 | 2,2932 |
| 4 | - | 3 | 39 | 189 | 0,197484 | 1,95 | 2,1475 | 0,1129 | 4,4988 | 4,6117 |
| 5 | - | 4 | 78 | 184 | 0,279285 | 3,9 | 4,1793 | 0,0850 | 17,3814 | 17,4664 |
| 6 | - | 5 | 34 | 231 | 0,184391 | 1,7 | 1,8844 | 2,1446 | 1,4063 | 3,5509 |
| 7 | - | 6 | 63 | 189 | 0,250998 | 3,15 | 3,4010 | 0,2831 | 11,2837 | 11,5668 |
| 8 | - | 7 | 44 | 179 | 0,209762 | 2,2 | 2,4098 | 0,0018 | 5,8052 | 5,8070 |
| 9 | - | 8 | 47 | 184 | 0,216795 | 2,35 | 2,5668 | 0,0321 | 6,5564 | 6,5884 |
| 10 | - | 9 | 42 | 181 | 0,204939 | 2,1 | 2,3049 | 0,0016 | 5,3111 | 5,3127 |
| 11 | - | 10 | 70 | 180 | 0,264575 | 3,5 | 3,7646 | 2,12721E-31 | 14,1720 | 14,1720 |
| 12 | - | 11 | 84 | 180 | 0,289828 | 4,2 | 4,4898 | 3,02578E-31 | 20,1586 | 20,1586 |
| 13 | - | 12 | 77 | 180 | 0,277489 | 3,85 | 4,1275 | 2,55711E-31 | 17,0362 | 17,0362 |
| 14 | - | 13 | 42 | 180 | 0,204939 | 2,1 | 2,3049 | 7,97437E-32 | 5,3127 | 5,3127 |
| 15 | - | 14 | 71 | 180 | 0,266458 | 3,55 | 3,8165 | 2,18624E-31 | 14,5654 | 14,5654 |
| 16 | - | 15 | 71 | 180 | 0,266458 | 3,55 | 3,8165 | 2,18624E-31 | 14,5654 | 14,5654 |
| 17 | - | 16 | 58 | 184 | 0,240832 | 2,9 | 3,1408 | 0,0480 | 9,8168 | 9,8648 |
| 18 | - | 17 | 12 | 199 | 0,109545 | 0,6 | 0,7095 | 0,0534 | 0,4501 | 0,5035 |
| 19 | - | 18 | 68 | 241 | 0,260768 | 3,4 | 3,6608 | 10,2514 | 3,1498 | 13,4012 |
| 20 | - | 19 | 57 | 180 | 0,238747 | 2,85 | 3,0887 | 0,0000 | 9,5404 | 9,5404 |
| 21 | - | 20 | 36 | 106 | 0,189737 | 1,8 | 1,9897 | 3,6583 | 0,3008 | 3,9591 |
| 22 | - | 21 | 37 | 271 | 0,192354 | 1,85 | 2,0424 | 4,1699 | 0,0013 | 4,1712 |
| 23 | - | 22 | 31 | 182 | 0,176068 | 1,55 | 1,7261 | 0,0036 | 2,9757 | 2,9793 |
| 24 | - | 23 | 105 | 359 | 0,324037 | 5,25 | 5,5740 | 0,0095 | 31,0604 | 31,0699 |
| 25 | - | 24 | 38 | 214 | 0,194936 | 1,9 | 2,0949 | 1,3723 | 3,0164 | 4,3888 |
| 26 | - | 25 | 31 | 185 | 0,176068 | 1,55 | 1,7261 | 0,0226 | 2,9567 | 2,9793 |
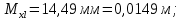
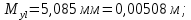
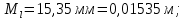
Подставляя найденные значения в формулы (6.1–6.4) получим:
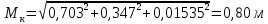
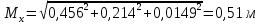
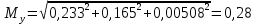 м
м
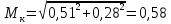 м
мСреднеквадратическая погрешность (СКП) положения наиболее удаленных пунктов опорной сети относительно исходных пунктов не должна превышать 0.4 мм на плане, т.е. 0.8 м для плана горных выработок масштаба 1:2000, т.е. Мк <Мдоп.
В нашем случае 0,8м = 0,8 м (для масштаба основного плана 1:2000), следовательно, необходимо скорректировать используемую методику.
6.3 Анализ точности угловых и линейных измерений при подземных маркшейдерских съемках
Прежде чем корректировать методику измерений проведем анализ точности угловых и линейных измерений для уточнения длины стороны теодолитной съемки и определения средней ошибки измерения горизонтального угла.

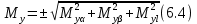
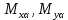 – средние погрешности координат, обусловленные погрешностью
– средние погрешности координат, обусловленные погрешностью  – ошибки координат в зависимости от ошибок измерения горизонтальных углов;
– ошибки координат в зависимости от ошибок измерения горизонтальных углов;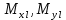 – ошибки координат, обусловленные ошибками измерения длин линий;
– ошибки координат, обусловленные ошибками измерения длин линий;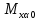 и
и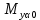 ) определяют по формулам:
) определяют по формулам: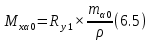
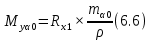
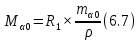
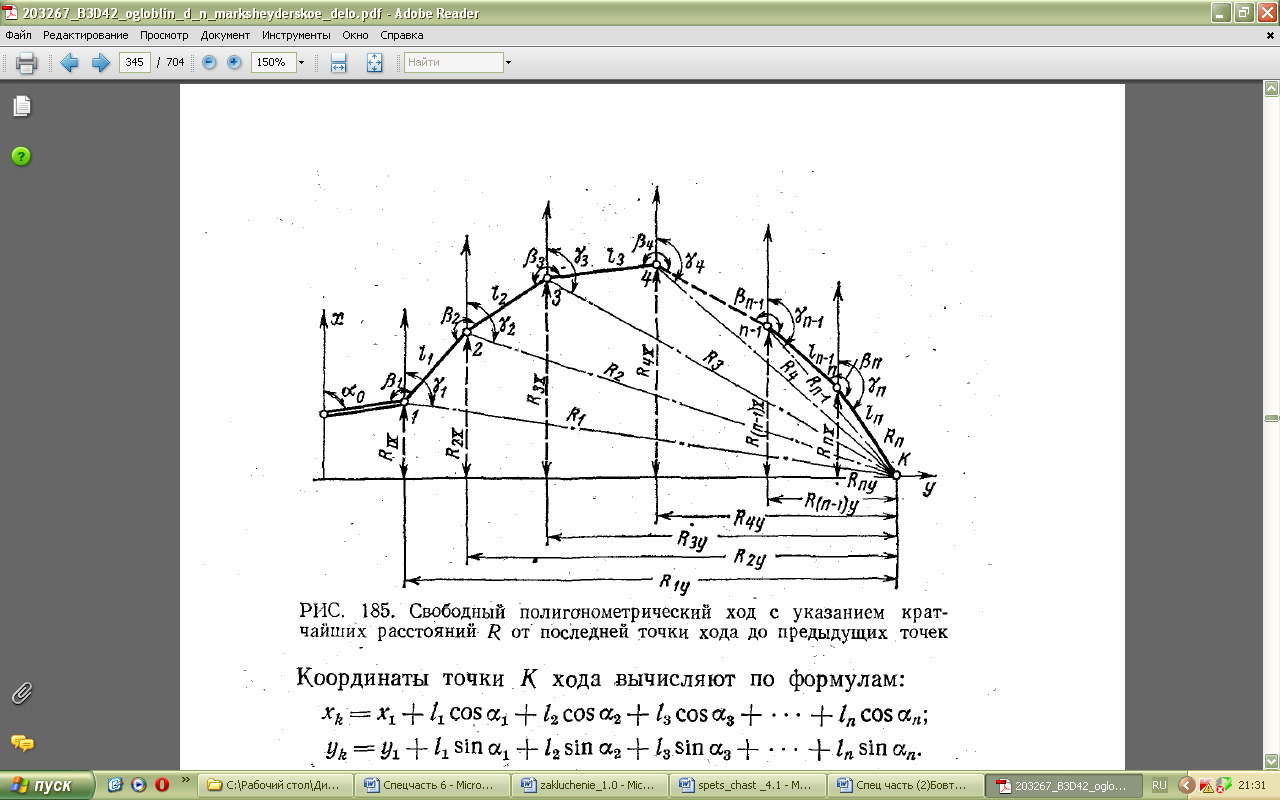
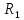 - кратчайшее расстояние от конечного пункта до первого (рис.);
- кратчайшее расстояние от конечного пункта до первого (рис.);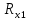 ,
,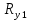 - проекции кратчайшего расстояния
- проекции кратчайшего расстояния 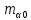 - погрешность дирекционного угла исходной стороны.
- погрешность дирекционного угла исходной стороны.