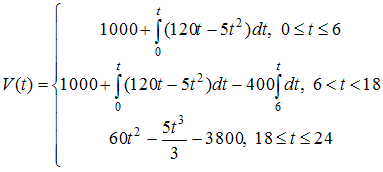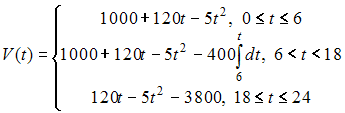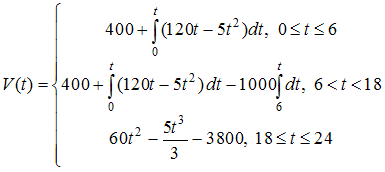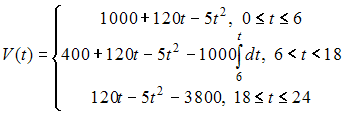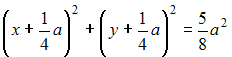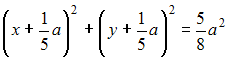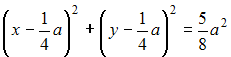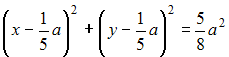Документ Microsoft Office Word (2). Специальность 080200. 62 Менеджмент Группа Мбзк11 Дисциплина Математика Логин 04ps2357934 Начало тестирования
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Начало формы Конец формы Общее решение системы дифференциальных уравнений 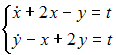 имеет вид … имеет вид …
Решение: Решим систему дифференциальных уравнений методом исключения. Из первого уравнения находим тогда производная и после подстановки выражений для и во второе уравнение системы получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами Поскольку правая часть исходного уравнения Так как не является корнем характеристического уравнения, то частное решение неоднородного уравнения будем искать в виде Найдя производные первого и второго порядков и подставив в уравнение Тогда общее решение этого уравнения имеет вид Значит, общее решение системы уравнений имеет вид ЗАДАНИЕ N 36 отправить сообщение разработчикам Кейс-задания: Кейс 1 подзадача 1 Начало формы Конец формы Для уборки снега на улицах города используются снегоуборочные машины. Они работают в течение светлого времени суток с 6 до 18 часов с постоянной скоростью уборки снега 400 Изменение объема снега, выпадающего на улицы города в городе в течение суток, можно описать уравнением В момент времени на улицах города лежит 1000 снега. Пусть – объем снега, лежащего на улицах города в момент времени t, тогда математическая модель для нахождения может иметь вид …
Решение: Скорость изменения объема снега , лежащего на улицах города, для равна 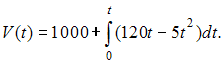 С 6 до 18 часов работают снегоуборочные машины с постоянной скоростью уборки снега 400 . Следовательно, С 6 до 18 часов работают снегоуборочные машины с постоянной скоростью уборки снега 400 . Следовательно, 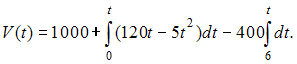 После 18 часов снегоуборочные машины не работают. Следовательно, 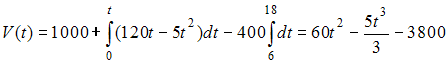 при при Поэтому 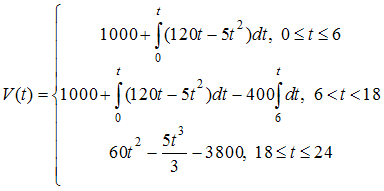 ЗАДАНИЕ N 37 отправить сообщение разработчикам Кейс-задания: Кейс 1 подзадача 2 Начало формы Конец формы Для уборки снега на улицах города используются снегоуборочные машины. Они работают в течение светлого времени суток с 6 до 18 часов с постоянной скоростью уборки снега 400 Изменение объема снега, выпадающего на улицы города в городе в течение суток, можно описать уравнением В момент времени на улицах города лежит 1000 снега. Установите соответствие между временем t и объемом снега, лежащего на улицах города 1. Объем снега, лежащего на улицах города в момент времени часов. 2. Объем снега, лежащего на улицах города в момент времени часов.
Решение: Так как 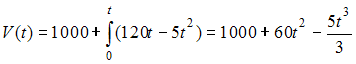 для то для то 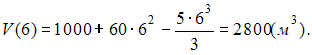 При При 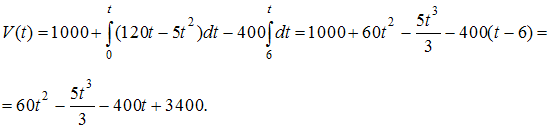 Тогда 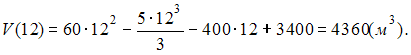 ЗАДАНИЕ N 38 отправить сообщение разработчикам Кейс-задания: Кейс 1 подзадача 3 Начало формы Конец формы Для уборки снега на улицах города используются снегоуборочные машины. Они работают в течение светлого времени суток с 6 до 18 часов с постоянной скоростью уборки снега 400 Изменение объема снега, выпадающего на улицы города в городе в течение суток, можно описать уравнением В момент времени на улицах города лежит 1000 снега. Пусть снегоуборочные машины не работали в обеденное время
Решение: В этом случае 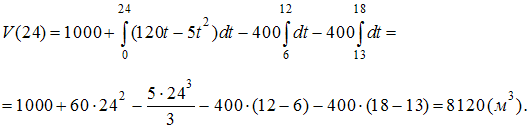 ЗАДАНИЕ N 39 отправить сообщение разработчикам Кейс-задания: Кейс 2 подзадача 1 Начало формы Конец формы В городском парке, имеющем форму квадрата со стороной a, установлены две осветительные установки A и B, расположенные в противолежащих вершинах этого квадрата (см. рисунок). 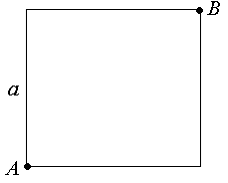 Устройство этих установок таково, что наилучшая освещенность на поверхности парка достигается в таких точках М, для которых выполняется условие Если ввести систему координат так, как показано на рисунке, то уравнение линии, на которой расположены все такие точки, может быть записано в виде … 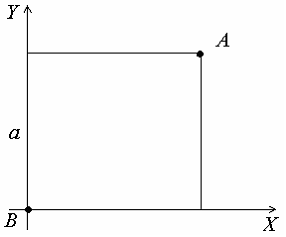
Решение: Введем систему координат, как показано на рисунке: начало координат совпадает с расположением установки B, оси ОХ и OY направлены по сторонам квадрата. Тогда точка А имеет координаты (a; a), точка B – (0;0). 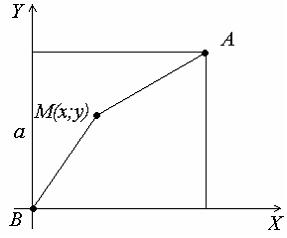 Пусть М(х,у) – точка, удовлетворяющая условию задачи (с наилучшей освещенностью). Тогда Следовательно, 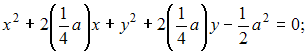 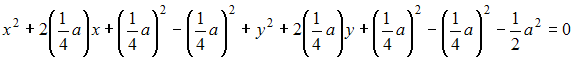 (выделяем полный квадрат); (выделяем полный квадрат);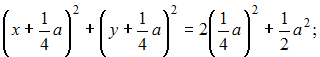 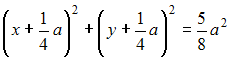 – уравнение окружности. – уравнение окружности.Все точки с наилучшей освещенностью лежат на окружности. ЗАДАНИЕ N 40 отправить сообщение разработчикам Кейс-задания: Кейс 2 подзадача 2 Начало формы Конец формы В городском парке, имеющем форму квадрата со стороной a, установлены две осветительные установки A и B, расположенные в противолежащих вершинах этого квадрата (см. рисунок).  Устройство этих установок таково, что наилучшая освещенность на поверхности парка достигается в таких точках М, для которых выполняется условие В местах пересечения этой дорожки со сторонами квадрата расположены входы в парк. Пусть сторона квадрата равна м. Тогда расстояние от установки B до ближайшего такого входа равно ____ м.
Решение: Окружность 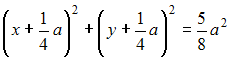 пересекает стороны квадрата в точках C и D, которые равноудалены от точки B (см. рисунок). пересекает стороны квадрата в точках C и D, которые равноудалены от точки B (см. рисунок).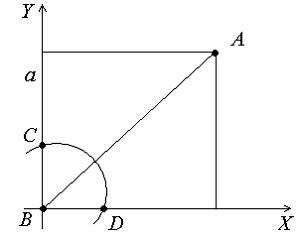 Расстояние BD равно абсциссе точки пересечения окружности с осью ОХ Решаем систему 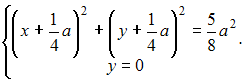 Следовательно, Следовательно,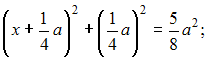 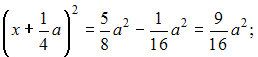 Так как абсцисса точки D положительна, то По условию задачи Тогда |