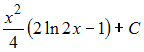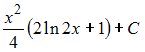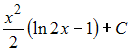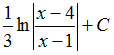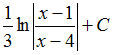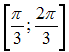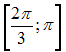Документ Microsoft Office Word (2). Специальность 080200. 62 Менеджмент Группа Мбзк11 Дисциплина Математика Логин 04ps2357934 Начало тестирования
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Тема: Непосредственное интегрирование Начало формы Конец формы Множество первообразных функции 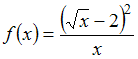 имеет вид … имеет вид …
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 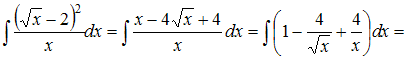 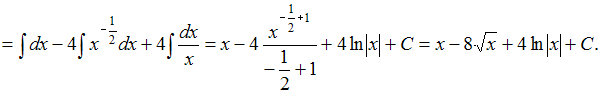 ЗАДАНИЕ N 13 отправить сообщение разработчикам Тема: Замена переменной в неопределенном интеграле Начало формы Конец формы Множество первообразных функции
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 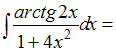 Произведем замену 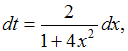 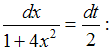 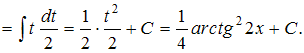 ЗАДАНИЕ N 14 отправить сообщение разработчикам Тема: Интегрирование по частям в неопределенном интеграле Начало формы Конец формы Множество первообразных функции
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 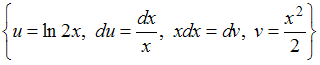 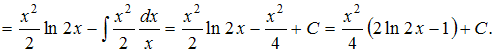 ЗАДАНИЕ N 15 отправить сообщение разработчикам Тема: Интегрирование рациональных функций Начало формы Конец формы Множество первообразных функции 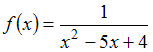 имеет вид … имеет вид …
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Разложив знаменатель дробно-рациональной функции на линейные множители, получаем 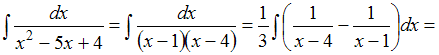 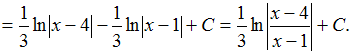 ЗАДАНИЕ N 16 отправить сообщение разработчикам Тема: Интегрирование иррациональных выражений Начало формы Конец формы Множество первообразных функции 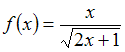 имеет вид … имеет вид …
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 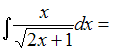 Произведем замену 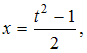 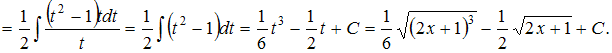 ЗАДАНИЕ N 17 отправить сообщение разработчикам Тема: Интегрирование тригонометрических функций Начало формы Конец формы Множество первообразных функции 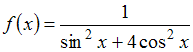 имеет вид … имеет вид …
Решение: Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда 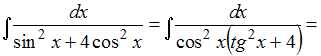 Произведем замену 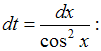 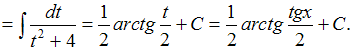 ЗАДАНИЕ N 18 отправить сообщение разработчикам Тема: Свойства определенного интеграла Начало формы Конец формы Значение определенного интеграла 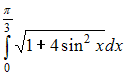 принадлежит промежутку … принадлежит промежутку …
Решение: Если функция интегрируема на и 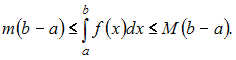 Согласно свойств функции наименьшее значение функции 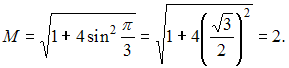 Следовательно, 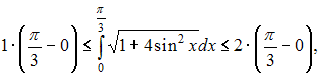 или или 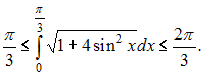 ЗАДАНИЕ N 19 отправить сообщение разработчикам |