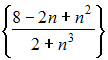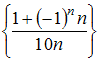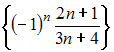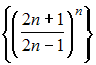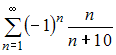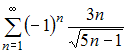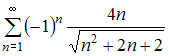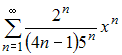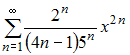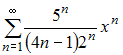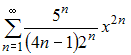Документ Microsoft Office Word (2). Специальность 080200. 62 Менеджмент Группа Мбзк11 Дисциплина Математика Логин 04ps2357934 Начало тестирования
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Тема: Методы вычисления определенного интеграла Начало формы Конец формы Определенный интеграл 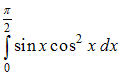 равен … равен …
Решение: Для вычисления данного определенного интеграла произведем замену переменных: Тогда 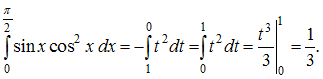 ЗАДАНИЕ N 20 отправить сообщение разработчикам Тема: Приложения определенного интеграла Начало формы Конец формы Площадь фигуры, изображенной на рисунке 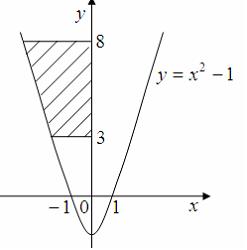 равна …
Решение: Площадь данной фигуры можно вычислить по формуле 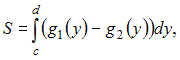 где где 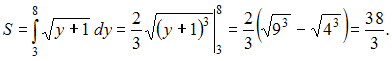 ЗАДАНИЕ N 21 отправить сообщение разработчикам Тема: Двойные интегралы Начало формы Конец формы Повторный интеграл 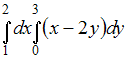 равен … равен …
Решение: Вычисление повторного интеграла вида 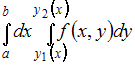 сводится к последовательному вычислению определенных интегралов с учетом того, что при вычислении интеграла вида сводится к последовательному вычислению определенных интегралов с учетом того, что при вычислении интеграла вида 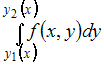 переменная x считается постоянной. Тогда переменная x считается постоянной. Тогда 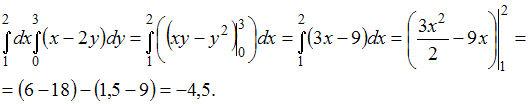 ЗАДАНИЕ N 22 отправить сообщение разработчикам Тема: Числовые последовательности Начало формы Конец формы Бесконечно малой является числовая последовательность …
Решение: Бесконечно малой последовательностью называется последовательность предел которой равен нулю, то есть Из предложенных последовательностей бесконечно малой является последовательность 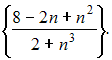 Действительно 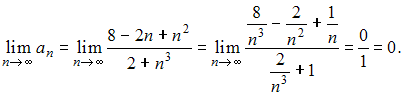 Остальные последовательности не являются бесконечно малыми, в чем легко убедиться, вычислив пределы общего члена. ЗАДАНИЕ N 23 отправить сообщение разработчикам Тема: Сходимость числовых рядов Начало формы Конец формы Сходящимся является числовой ряд …
Решение: Из представленных числовых рядов сходящимся является ряд 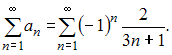 Действительно, при применении признака сходимости Лейбница, получаем: Действительно, при применении признака сходимости Лейбница, получаем:1) 2) для любого натурального справедливо 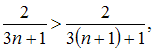 то есть последовательность Следовательно, ряд 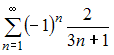 сходится. сходится.Для остальных рядов ЗАДАНИЕ N 24 отправить сообщение разработчикам Тема: Область сходимости степенного ряда Начало формы Конец формы Радиус сходимости равен 2,5 для степенного ряда …
Решение: Радиус сходимости равен 2,5 для степенного ряда 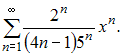 Действительно, Действительно,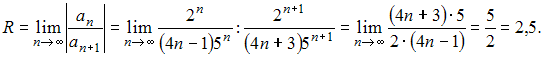 ЗАДАНИЕ N 25 отправить сообщение разработчикам Тема: Ряд Тейлора (Маклорена) Начало формы Конец формы Если
Решение: Так как коэффициенты данного ряда Тейлора вычисляются по формуле 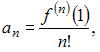 то вычислим последовательно производные: то вычислим последовательно производные:Тогда ЗАДАНИЕ N 26 отправить сообщение разработчикам Тема: Типы дифференциальных уравнений Начало формы Конец формы Уравнение
Решение: Уравнение ЗАДАНИЕ N 27 отправить сообщение разработчикам Тема: Поле направлений и изоклины Начало формы Конец формы Поле направлений дифференциального уравнения
Решение: Так как поле направлений дифференциального уравнения Тогда ЗАДАНИЕ N 28 отправить сообщение разработчикам |