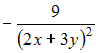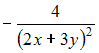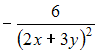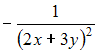Документ Microsoft Office Word (2). Специальность 080200. 62 Менеджмент Группа Мбзк11 Дисциплина Математика Логин 04ps2357934 Начало тестирования
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Тема: Производные первого порядка Начало формы Конец формы Производная функции 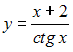 равна … равна …
Решение: 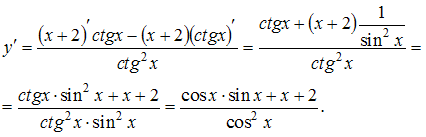 ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Производные высших порядков Начало формы Конец формы Функция задана в параметрическом виде 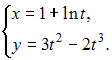 Тогда производная второго порядка функции по переменной x имеет вид … Тогда производная второго порядка функции по переменной x имеет вид …
Решение: Производная второго порядка функции заданной в параметрическом виде, по переменной x вычисляется по формуле: 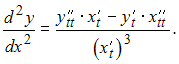 Вычислим последовательно 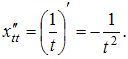 Тогда 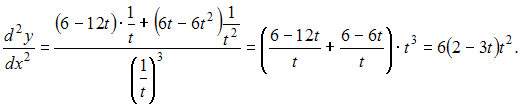 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Дифференциалы и теоремы о дифференцируемых функциях Начало формы Конец формы Предел 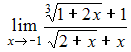 равен … равен …
Решение: Для вычисления данного предела применим правило Лопиталя, для чего воспользуемся формулой вида 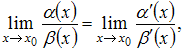 то есть то есть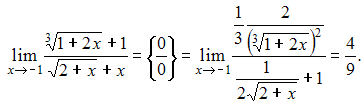 ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Приложения дифференциального исчисления ФОП Начало формы Конец формы К графику функции в его точке с абсциссой проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …
Решение: Уравнение касательной к графику функции в его точке с абсциссой имеет вид Тогда уравнение касательной примет вид Эта прямая пересекает оси координат в точках и то есть отсекает на осях координат отрезки, длины которых равны 2 и 4. Следовательно, площадь соответствующего прямоугольного треугольника равна: ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Асимптоты графика функции Начало формы Конец формы Вертикальная асимптота графика функции 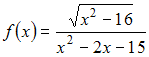 задается уравнением вида … задается уравнением вида …
Решение: Прямая является вертикальной асимптотой графика функции если эта функция определена в некоторой окрестности точки и Вычислим односторонние пределы функции в точке 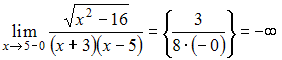 и и 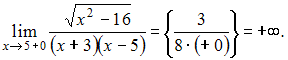 Следовательно, прямая будет вертикальной асимптотой. ЗАДАНИЕ N 9 отправить сообщение разработчикам Тема: Частные производные первого порядка Начало формы Конец формы Частная производная функции
Решение: При вычислении частной производной по переменной переменные и рассматриваем как постоянные величины. Тогда ЗАДАНИЕ N 10 отправить сообщение разработчикам Тема: Частные производные высших порядков Начало формы Конец формы Частная производная второго порядка функции
Решение: При вычислении частной производной функции 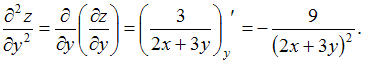 ЗАДАНИЕ N 11 отправить сообщение разработчикам Тема: Полный дифференциал ФНП Начало формы Конец формы Приближенное значение функции
Решение: Воспользуемся формулой 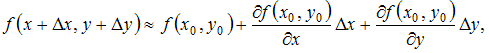 где Вычислим последовательно 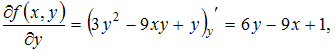 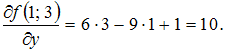 Тогда ЗАДАНИЕ N 12 отправить сообщение разработчикам |