соч геометрия 11. Спецификация суммативного оценивания за четверть по предмету Геометрия

• Название: Спецификация суммативного оценивания за четверть по предмету Геометрия
• Анкор: соч геометрия 11
• Дата: 07.04.2023
• Размер: 372.17 Kb.
• Имя файла: SOCh_Geometria_11_klass_EMN_rus.docx
• Тип: Документы; #1043881
• страница: 9 из 11

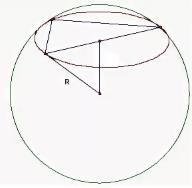
Образец заданий и схема выставления баллов

Задания суммативного оценивания за 3 четверть по предмету «Математика»

1. 
   Вершины прямоугольного треугольника лежат на сфере радиусом 6 см.
   
   1. 
      Выполните рисунок по условию задачи.
      

2. 
   Найдите расстояние от центра сферы до плоскости треугольника, если его гипотенуза равна 4 см.
   

[1]

[2]

2.

1. 
   Круговой сектор радиуса 12 ограничен дугой с градусной мерой 135 . Вычислите площадь данногосектора.
   

[2]

2. 
   Сектор свернули в конус. Используя результат предыдущего пункта, найдите радиус конуса.
   

[2]

3. 
   Мячик для настольного тенниса имеет радиус 20 мм. Мячи плотно укладывают в пластиковый контейнер по 6 штук, как показано на рисунке. (Мячи касаются дна, стенок и крышки контей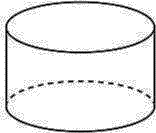нера)
   

Крышка контейнера также имеет форму цилиндра радиусом 21 мм, высотой 15 мм. Рассчитайте площадь пластика, необходимого для изготовления одного контейнера.

[4]

3. 
   Диагональ осевого сечения усеченного конуса является биссектрисой острого угла при основании этого сечения. Образующая равна 8 и образует угол 60 с плоскостью основания. Выполнив рисунок, найдите площадь полной поверхности усеченного конуса.
   

[4]


21

3. 
   Параллельно оси цилиндра проведено сечение, площадь которого равна S, а диагональ ^{сечения образует с плоскостью основания угол}  ^{. Сечение пересекает нижнее основание} цилиндра по хорде, которую видно из центра этого основания под углом  .
   

Выполните рисунок по условию задачи. Найдите:

1. 
   высоту цилиндра;
   

2. 
   радиус основания цилиндра.
   

[3]
[2]

Схема выставления баллов

№	Ответ	Балл	Дополнительная информация
1 a		1	Выполнен рисунок по условию задачи
1 b	Показано, что центр сечения совпадает с серединой гипотенузы треугольника. Показан метод нахождения искомого расстояния.	1
	4 2	1
2	135  122 360	1	За использование формулы площади кругового сектора
	54	1
	r12  54	1	Балл выставляется со своимзначением площади кругового сектора
	r 4, 5	1
3	Высота цилиндра 24 см, радиус основания 2 см	1
	4  24 4	1	За использование формулы площадей круга и прямоугольника
	2,12 1, 5 4, 2	1
	110, 71	1
4	Выполнен рисунок по условию задачи	1
	Радиус верхнего основания равен 4	1
	Радиус нижнего основания равен 8	1
	Sполн.  176	1
5 a	Выполнен рисунок по условию задачи, указаны углы из условия задачи	1
	Показан метод нахождения высоты цилиндра	1
	S tg	1
5 b	Показан метод нахождения радиуса цилиндра	1
	S ctg 2 sin  2	1
Итого:		20