Ипанова Н.В. Сравнительный анализ моделей оценки вероятности банкротства (7). Ипанова Н.В. Сравнительный анализ моделей оценки вероятности бан. Сравнительный анализ моделей оценки вероятности банкротства для российских компаний

• Название: Сравнительный анализ моделей оценки вероятности банкротства для российских компаний
• Анкор: Ипанова Н.В. Сравнительный анализ моделей оценки вероятности банкротства (7
• Дата: 09.01.2021
• Размер: 0.89 Mb.
• Имя файла: Ипанова Н.В. Сравнительный анализ моделей оценки вероятности бан.docx
• Тип: Документы; #166655
• страница: 2 из 10

Оценка вероятности банкротства современных исследователей.

Автор и год исследования	Метод	Данные	Вид функции/ Ошибки I и II рода	Результаты
Э. Альтман, 2005 [11, C. 2679-2714]	ДА	Мексиканские компании, данные с 1994 года	EM Score = 6,56∙X1 + 3,26∙X2 + 6,72∙X3 + 1,05∙X4 + 3,25	Точность прогнозирования модели составляет 72%.
Э. Альтман, 2010 [22, C. 220-236]	ДА	Китайские компании, 30 банкротов и 30 небанкротов, 1998-1999 гг. (исследования кризиса)	ZCHINA = 0,517 – 0,46∙X1 + 9,32∙X2 + 0,388∙Х3 + 1,158∙Х4	Точность прогнозирования модели составляет около 70%.
Д. Чессер [14, C.28-38]	ЛГ	37 компаний-банкротов и 37 небанкротов	Z = 1 / (1+e-y) Y = -2,0434 – 5,24∙X1 + 0,0053∙X2 – 6,6507∙X3 + 4,4009∙X4 – 0,0791∙X5 – 0,1220∙X6	Модель работает в 75% случаев
В. А. Журов, 2007 [4, C. 53 – 65]	Однофакторный анализ, ДА, Анализ условной вероятности, дерево решений, НС	Японские компании, 210 банкротов и 210 небанкротов, данные с 1995 по 2002 гг.	Наибольшая ошибка первого рода встречается у однофакторного анализа, затем – при использовании дерева решений. Ошибка второго рода наиболее высока при использовании ДА и однофакторного анализа.	Общая точность классификации исходного набора данных наиболее высока при использовании нейронных сетей и дерева решений (больше 95%), при использовании ДА точность прогнозирования составляет 85,3%.
К. М. Тотьмянина, 2011[7, C. 59 – 68]	ЛГ	36 российских компаний-банкротов и 36 небанкротов, 2005-2009 гг.	Ошибки первого рода: 16,7% Ошибки второго рода: 11%	Модель работает в 86% случаев
Ф. Д. Жардин, 2012 [17, C.20 – 39]	ДА, ЛГ, НС	250 французских компаний-банкротов и 250 небанкротов, 2002 г.	-	Точность модели, построенной с помощью НС – 88,92%, ЛГ – 86,02% и ДА – 83,86%

1.4 Применение существующих методик оценки вероятности дефолта для российских компаний

Рассмотренные выше методики из зарубежной практики достаточно популярны в сфере корпоративного кредитования благодаря своей доступности и высокой точности прогнозирования. Однако применение вышеперечисленных моделей для российской переходной экономики  затруднено. Это вызвано, прежде всего:

1. 
   Различием статистической выборки предприятий при формировании модели: компании разных стран имеют свои отличительные особенности, поэтому основа – база данных – играет ключевую роль в моделировании;
   
2. 
   Различие в учете отдельных показателей: так, например, в США используется система бухгалтерской отчетности по стандартам GAAP (англ. Generally Accepted Accounting Principles – общепринятые принципы бухгалтерского учета), которая существенно отличается от российских стандартов бухгалтерского учета (в РСБУ жесткая регламентация деятельности бухгалтеров, единый план счетов и т.д.);
   

Тем не менее, экономисты из множества стран, проверяющие на практике данные модели, соглашаются с их универсальностью и надежностью. Адаптировав веса при коэффициентах в моделях для своих государств и отраслей множество экономистов сходятся в ее высокой работоспособности и статистической надежности. Поэтому для создания моделей прогнозирования наступления дефолта для российских предприятий, была собрана база данных финансовой отчетности отечественных компаний, на основе которой был произведен более точный анализ кредитоспособности российских корпоративных заемщиков.

2. Разработка моделей оценки вероятности банкротства для российских компаний
2.1 Описание выборки

Для разработки моделей было отобрано 240 наблюдений: 120 обанкротившихся компаний и 120 успешно работающих компаний. Были найдены предприятия, которые объявили дефолт в 2012-2013 гг., и в пару к каждому банкроту была отобрана аналогичная компания, схожая по размерам активов и отрасли, не объявлявшая о банкротстве и функционирующая на сегодняшний день. Из всех отраслей были выбраны промышленные сферы деятельности, а именно:

• 
  производство передача и распределение электроэнергии;
  
• 
  добыча и переработка нефти, газа и смежные производства;
  
• 
  металлургическое производство;
  
• 
  химическое производство;
  
• 
  производство прочих неметаллических минеральных продуктов.
  

По 240 наблюдениям были собраны данные годовой финансовой отчетности – бухгалтерского баланса и отчета о прибылях и убытках – за 2009 год, так как считается, что за 3-4 года до дефолта компания еще «здоровая», а значит, и данные представляют собой бόльшую ценность. База данных была собрана с сайта Первого Независимого Рейтингового Агентства – FIRA.RU, а анализ выборки был произведен в статистическом пакете SPSS Statistics. По данным бухгалтерской отчетности были рассчитаны чаще всего используемые аналитиками финансовые показатели:

1. 
   Коэффициент текущей ликвидности.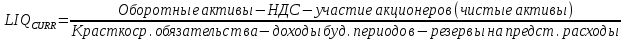
   

(14)

Данный коэффициент показывает, сколько оборотных средств приходится на единицу текущей краткосрочной задолженности и дает общую оценку ликвидности компании.

2. 
   Коэффициент промежуточного покрытия (срочной ликвидности)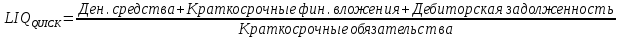
   

(15)

Данный показатель характеризует краткосрочные заемные обязательства, которые компания сможет погасить за счет наиболее ликвидных активов и погашения краткосрочной дебиторской задолженности.

3. 
   Коэффициент абсолютной ликвидности.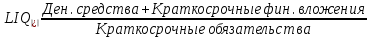
   

(16)

Показывает долю заемных средств, которую компания сможет погасить быстрее благодаря реализации наиболее ликвидных активов.

4. 
   Доля чистого оборотного капитала (ЧОК) в активах.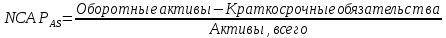
   

(17)

ЧОК показывает, какая часть оборотных средств финансируется благодаря собственным активам предприятия.

5. 
   Доля денежных средств в активах.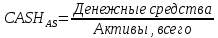
   

(18)

Денежные средства и их эквиваленты являются наиболее ликвидными активами компании.

6. 
   Коэффициент автономии (финансовой независимости).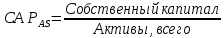
   

(19)

Данный показатель показывает долю собственных источников финансирования в балансе.

7. 
   Коэффициент финансовой устойчивости.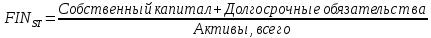
   

(20)

Показывает долю долгосрочных источников финансирования в общей валюте баланса.

8. 
   Коэффициент финансовой активности.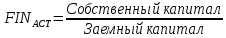
   

(21)

Характеризует соотношения собственного и заемного капитала.

9. 
   Отношение обязательств к активам компании.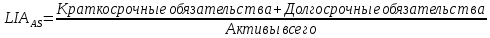
   

(22)

Показывает долю обязательств компании, которые покрываются активами компании.

10. 
    Коэффициент устойчивости экономического роста компании.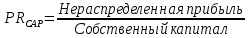
    

(23)

Данный показатель характеризует долю нераспределенной прибыли (убытка) в собственном капитале предприятия.

11. 
    Коэффициент маневренности.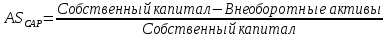
    

(24)

Коэффициент отражает долю собственного капитала, которая приходится на наиболее ликвидные активы компании.

12. 
    Коэффициент обеспеченности запасов и затрат собственным средствам.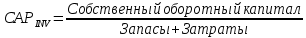
    

(25)

Отражает возможность покрытия запасов и затрат из средств собственного оборотного капитала.

13. 
    Отношение нераспределенной прибыли к активам.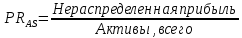
    

(26)

Отражает долю активов, которая покрывается за счет нераспределенной прибыли (убытка) отчетного периода.

14. 
    Рентабельность активов.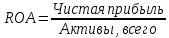
    

(27)

Показывает долю чистой прибыли, приходящуюся на единицу активов компании и характеризует эффективность использования активов компании для генерации выручки.

15. 
    Рентабельность продаж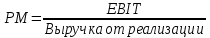
    

(28)

Показывает, сколько операционной прибыли приходится на единицу выручки.

16. 
    Коэффициент маржинальной прибыли (коэффициент вклада на покрытие).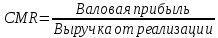
    

(29)

Характеризует валовую прибыль на единицу выручки от реализации, является мерой операционного рычага.

17. 
    Рентабельность вложенного капитала.
    

(30)

Характеризует отдачу на вложенный капитал с точки зрения учетной прибыли.

18. 
    Рентабельность собственного капитала.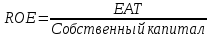
    

(31)

Характеризует эффективность использования капитала и показывает, сколько предприятие имеет чистой прибыли с рубля авансированного в капитал.

19. 
    Коэффициент покрытия процентов.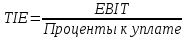
    

(32)

Показывает возможную степень снижения операционной прибыли предприятия, при которой оно может обслуживать выплаты процентов. 

20. 
    Отношение выручки к активам.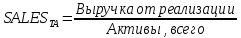
    

(33)

Характеризует эффективность, с которой компания использует все имеющиеся ресурсы.

Следует отметить, что у переменной TIE (коэффициент покрытия процентов) больше 30% пропущенных данных. Это можно объяснить тем, что у многих компаний отсутствует задолженность по процентам к уплате. Поэтому данную переменную было целесообразно исключить из выборки.
2.2 Исследование выборки

После формирования выборки для детального анализа данных были выполнены следующие процедуры:

• 
  проверка нормальности распределения с помощью описательных статистик и графического анализа;
  
• 
  выявление экстремальных значений с помощью графического и разведочного анализов и исключение выбросов;
  
• 
  выявление наиболее дескриптивных переменных с помощью тестов Стьюдента, Манна-Уитни, однофакторного дисперсионного анализа;
  
• 
  корреляционный анализ переменных.
  

Из описательных статистик переменных (Приложение 1) видно, что разброс между минимумом и максимумом очень большой у каждого финансового показателя, что уже говорит о наличии выбросов. Коэффициент асимметрии у каждого показателя не близок к нулю, причем, отклонения существенны, а значит, распределения не симметричны и не являются нормальными [1, c. 108]. Коэффициент эксцесса характеризует остроту пика распределения, и в нашем случае пик распределения около математического ожидания для всех переменных острый, так как коэффициент больше нуля.

Далее был проведен графический анализ каждой переменной, который по каждому финансовому коэффициенту показал наличие выбросов – наблюдений, которые выделяются из общей выборки. Разведочный анализ выбросов (Приложение 2) и ящичковые диаграммы (Приложение 3) более детально показали количество аномальных наблюдений. Такие выделяющиеся наблюдения обычно возникают из-за ошибок измерения, необычной природы первоначальных данных или могут быть частью распределения и зачастую существенно влияют на качество модели, поэтому экстремальные наблюдения (данные по 16 компаниям) были исключены из выборки.

Следующим этапом анализа выборки является проверка на нормальность распределения. Коэффициенты асимметрии и эксцесса уже показали нам, что у каждого финансового показателя распределение ненормальное, также был проведен графический (Приложение 4) и аналитический анализ. Графики Q-Q (квантиль-квантиль, Приложение 5) для каждого показателя оценивают эмпирические значения и соответствующие им математические ожидания. Получившиеся вероятностные графики свидетельствуют об отклонениях от нормального распределения, так как во всех случаях график значений переменной отклоняется от прямой. Данный факт дает меньше шансов признать вид распределения нормальным, что подтверждает полученные ранее результаты: каждый финансовый показатель в выборке имеет существенные отклонения от нормального распределения. Важно отметить, что в дискриминантном анализе существует ограничение, связанное с нормальностью распределения переменных, однако на практике данное условие едва ли выполнимо, поэтому большинство исследователей опускают данную предпосылку.
2.3. Отбор риск-доминирующих показателей для оценки вероятности дефолта

Следующий этап – выбор наиболее дескриптивных переменных. Для сравнения значений каждого финансового показателя в двух группах выборки был применен t-критерий Стьюдента (Приложение 6). Группирующая переменная – bankruptcy, которая разделяет всю выборку на две группы: банкроты (0) и небанкроты (1). Доверительный интервал задается по умолчанию 95%. Данный тест сначала проверяет равенство дисперсий с помощью критерия Левина (Levene test). Выдвигаются две гипотезы:

Н₀: дисперсии в изучаемых группах равны;

Н₁: дисперсии не равны.

Если значимость больше 5%, то принимается нулевая гипотеза о равенстве дисперсий. И следующие результаты применения t-критерия Стьюдента необходимо смотреть в первой строке (где предполагается равенство дисперсий). В свою очередь t-критерий выдвигает следующие гипотезы:

Н₀: отсутствие различий между групповыми средними;

Н₁: групповые средние не равны.

Аналогично критерию Левина если уровень значимости больше 5%, то принимается нулевая гипотеза о равенстве групповых средних. Таким образом, согласно применению t -критерия Стьюдента групповые средние не имеют различий у следующих показателей:

• 
  коэффициент текущей ликвидности;
  
• 
  коэффициент финансовой устойчивости;
  
• 
  коэффициент устойчивости экономического роста;
  
• 
  отношение нераспределенной прибыли к активам;
  
• 
  коэффициент вклада на покрытие;
  
• 
  рентабельность продаж;
  
• 
  рентабельность активов;
  
• 
  рентабельность капитала;
  
• 
  отношение выручки к активам.
  

Однако следует заметить требование данного теста о нормальности распределения показателей, что выполняется лишь в редких случаях. Все финансовые показатели нашего исследования не имеют нормальное распределение, поэтому результаты t-критерия Стьюдента можно подвергнуть сомнению. Более того, для сравнения двух независимых выборок – банкротов и небанкротов – был применен непараметрический тест Манна-Уитни (Приложение 7). Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны. Как показал критерий Манна-Уитни, в нашем случае разница показателей не является статистически значимой (р > 5%) для следующих показателей:

• 
  коэффициент устойчивости экономического роста;
  
• 
  коэффициент вклада на покрытие;
  
• 
  рентабельность продаж;
  
• 
  рентабельность активов;
  
• 
  отношение выручки к активам.
  
• 
  рентабельность капитала;
  
• 
  отношение выручки к активам.
  

Результаты отличаются от t-критерия Стьюдента – тест Манна-Уитни дал меньшее количество дескриптивных показателей, однако нужно учитывать слабую значимость t-критерия в силу ненормального распределения.

Далее был проведен однофакторный дисперсионный анализ – ANOVA, Analysis of Variation (Приложение 8). Целью данного анализа является проверка значимости различия между средними в разных группах с помощью сравнения дисперсий этих групп. Выдвигаются две гипотезы:

Н₀: средние значения показателей между группами равны;

Н₁: есть существенные различия между средними.

Если значимость больше 5%, то принимается нулевая гипотеза о равенстве средних. Дисперсионный анализ показал, что средние значения равны для следующих показателей:

• 
  коэффициент текущей ликвидности;
  
• 
  коэффициент абсолютной ликвидности;
  
• 
  коэффициент финансовой устойчивости;
  
• 
  коэффициент устойчивости экономического роста;
  
• 
  коэффициент обеспеченности запасов и затрат собственным средствам;
  
• 
  коэффициент маневренности;
  
• 
  отношение нераспределенной прибыли к активам;
  
• 
  коэффициент вклада на покрытие;
  
• 
  рентабельность продаж;
  
• 
  рентабельность активов;
  
• 
  рентабельность капитала;
  
• 
  отношение выручки к активам.
  

Для изучения взаимосвязи показателей был проведен корреляционный анализ (Приложение 9). Коэффициент корреляции Пирсона — это параметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений, вычисляется по формуле [1, c. 109]: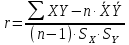

, (34) Где: ΣXY – сумма произведений данных из каждой пары;

n – число пар;

S_x — стандартное отклонение для распределения х;

S_y — стандартное отклонение для распределения у.

Как мы видим из таблицы парных корреляций, присутствует мультиколлинеарность (наличие сильной зависимости) между переменными: коэффициент текущей ликвидности, коэффициент срочной ликвидности, коэффициент абсолютной ликвидности, доля чистого оборотного капитала в активах. Также заметна сильная корреляция со многими показателями у следующих коэффициентов: коэффициент финансовой устойчивости, коэффициент финансовой активности, отношение обязательств к активам, отношение нераспределенной прибыли к активам, рентабельность активов.

Включение взаимозависимых переменных приводит к неопределенности и неидентифицируемости модели, поэтому так важно смотреть на зависимость переменных при выборе объясняющих факторов.
Таким образом, можно сделать вывод о том, что наиболее точно разделяют компании на банкротов и небанкротов следующие показатели:

1. 
   Коэффициент текущей ликвидности;
   
2. 
   Коэффициент устойчивости экономического роста;
   
3. 
   Коэффициент финансовой устойчивости;
   
4. 
   Рентабельность продаж;
   
5. 
   Отношение выручки к активам.