средства и методы в управлении качеством. Средства и методы УП. Средства и методы управления качеством

• Название: Средства и методы управления качеством
• Анкор: средства и методы в управлении качеством
• Дата: 30.04.2022
• Размер: 5.68 Mb.
• Имя файла: Средства и методы УП.doc
• Тип: Документы; #505246
• страница: 45 из 60

15.1. Параметрические методы

Научно-техническое направление надежность прошло в своем развитии ряд этапов. На начальном этапе для обеспечения надежности использовали запасы прочности, однако они часто приводили к увеличению габаритов и массы изделий и соответственно к дополнительному расходу материалов. Стремление уменьшить нежелательные эффекты стимулировало изучение реальных нагрузок на изделие при эксплуатации, несущей способности материалов и конструкций, процессов изменения их состояния вследствие старения, усталости и других факторов. Основой для решения задач по обеспечению надежности явились теория вероятностей и математическая статистика. На их базе позже установлена статистическая природа коэффициентов запаса прочности (работоспособности) и сформулировано понятие отказа как превышения нагрузки над прочностью.

В реальных изделиях часто наблюдается случайность в рас­пределении прочности конструкции и действующей нагрузки. Случайность в распределении прочности обусловлена допусками на физико-механические свойства материала и геометрические параметры конструкции. Случайность в распределении нагрузки вызвана нестабильностью эксплуатационной ситуации (окружающей среды). Расчет сводится к оценке истинных гипотез комбинированных событий и нахождению случайности в распределении событий параметрического прогнозирования. Оба события (распределение нагрузки и прочности конструкции) являются истинными, и совместность их проявления оценивается коэффициентом работоспособности. Если принять, что наблюдается нормальное распределение, то в критическом случае выбора показателя работоспособности происходит наложение площадей, ограниченных кривыми рассеяния нагрузки и прочности. Область наложения площадей кривых Sсоответствует вероятности отказа. Ситуация с использованием вероятностей значительно отличается от случая, когда учитывается лишь запас прочности. Вероятность отказа может быть совершенно различной при одном и том же за­пасе прочности, при разных формах кривых (или разных средних квадратических отклонениях), при различных нагрузках и прочности материала. Существенно новый подход к формированию качества изделий с учетом надежности требует принимать в расчет вероятностное распределение свойств нагрузки и конструкций. Гарантией надежной работы изделия служит тот случай, когда математическое ожидание прочности превышает математическое ожидание нагрузки; при этом допускается некоторое наложение площадей кривых распределения, вычисляемых с помощью нормальной функции распределения Ф(z). Известно, что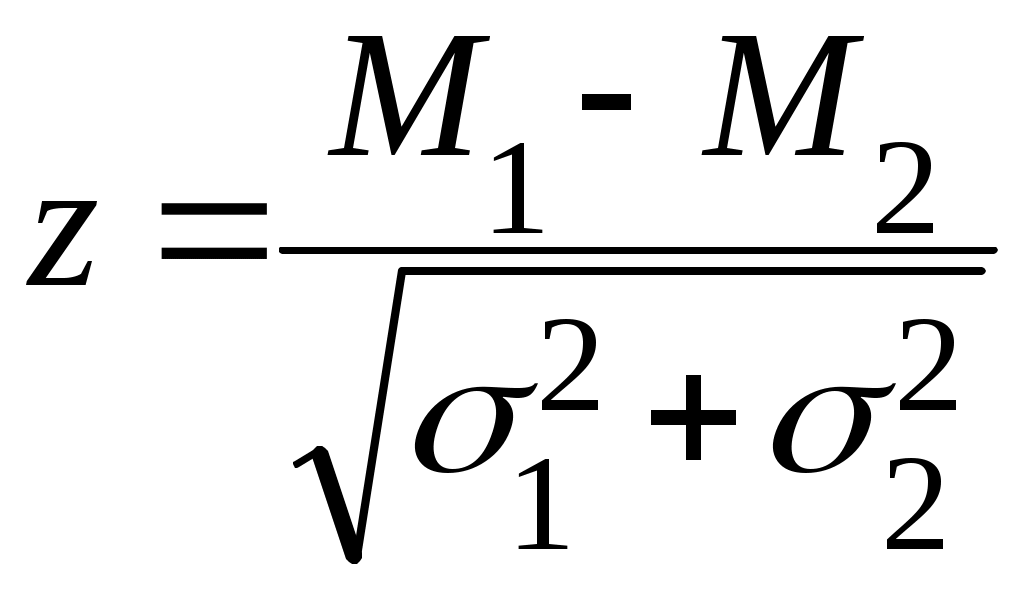

, (32)

где М₁и М₂ – математическое ожидание; σ₁и σ₂ – среднеквадратическое отклонение прочности и нагрузки соответственно.

Воспользовавшись табличными данными Ф(z), найдем в простой математической форме приближенную связь между zи Ф(z):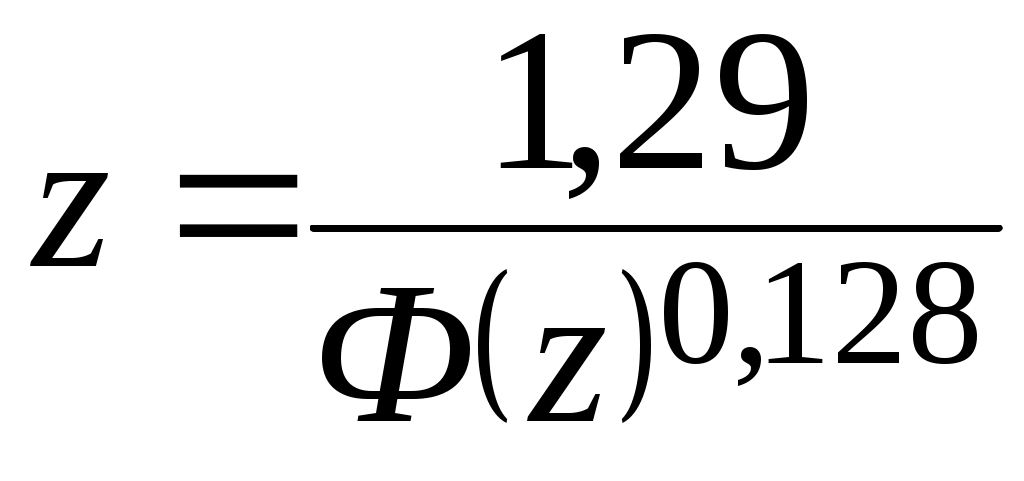

. (33)

Эта связь в сравнении с точной функцией дает хоро­шую сходимость результатов для интервала функции 0,01 ≤ Ф(z) < 0,04 с ошибкой менее 2 %. Объединив выражения (32) и (33) и приняв отношение М₁/М₂ = п за величину коэффициента работоспособности, получим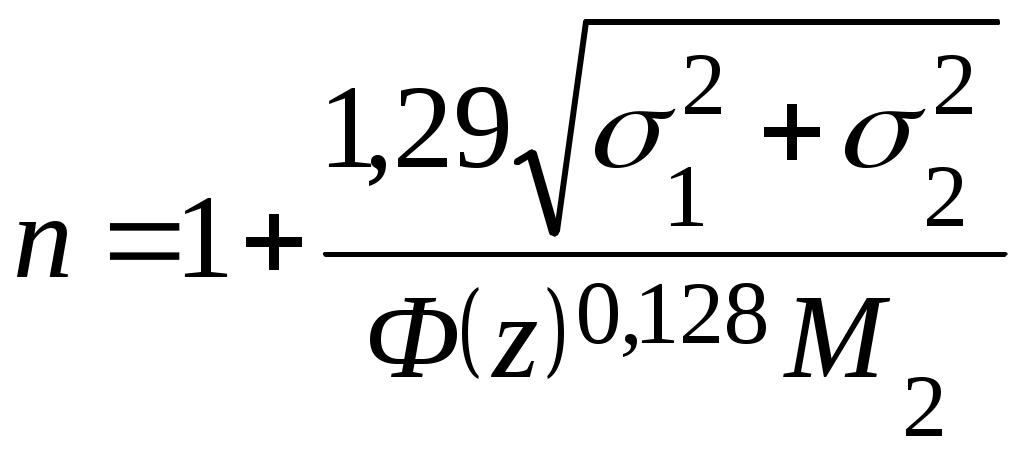

. (34)

Выводы относятся к механическим свойствам материала деталей, которые не изменяются с течением времени.

15.2. Структурные методы

При повышении надежности технической системы изделия, состоящей из множества элементов, часто бывает недостаточным повысить надежность элементов, поэтому необходимо применять резервирование,которое позволяет уменьшить вероятность отказов на несколько порядков. Применяют постоянное резервирование с нагруженным резервом и резервирование замещением с ненагруженным резервом.

Резервирование наиболее широко применяют в радио­электронной аппаратуре, в которой резервные элементы имеют малые габаритные размеры и легко переключаются.

Можно выделить следующие особенности резервирования в машиностроении: в некоторых системах резервные агрегаты используют как рабочие в часы пик; в ряде систем резервирование обеспечивает сохранение работоспособности, но с пониженными показателями.

В транспортных машинах, в частности в автомобилях, применяют двойную или тройную систему тормозов. В пассажирских самолетах применяют 3 или 4 двигателя и несколько электрических машин. Выход из строя одной или даже нескольких машин, кроме последней, не приводит к аварии самолета. Число эскалаторов, паровых котлов выбирают с учетом возможности отказа и необходимости ремонта. На заводах стараются иметь два или более уникальных станков основного производства. Применение запасных деталей также можно рассматривать как вид резервирования.

Идею резервирования легко проиллюстрировать на примере систем электрических цепей с ключами (рис. 32).

Допустим, что система электрической цепи состоит из двух ключей. Замыкание цепи можно осуществить лишь тогда, когда оба ключа работают нормально. Если надежность каждого ключа при выполнении операции замыкания цепи равна R,то надежность системы, состоящей из двух ключей, равна R²(см. риc. 32, a).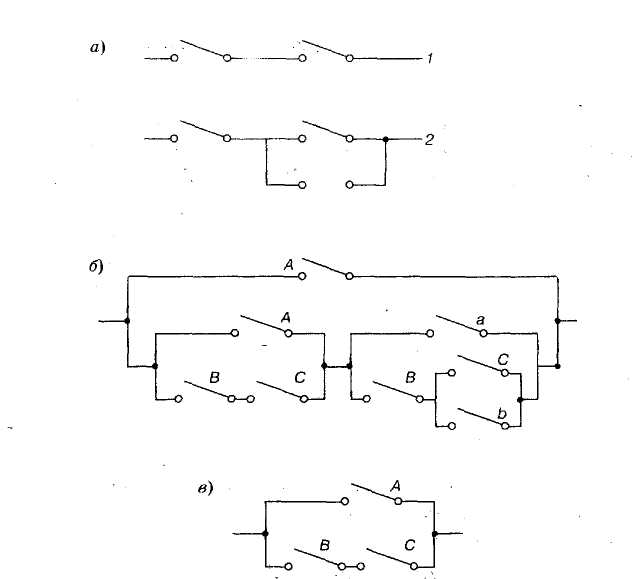

Рис. 32. К расчету резервирования элементов:

а – цепь из двух ключей: 1 – надежность системы равна R²; 2 – надежность системы равна R²(2 - R); б – сложная цепь; в – эквивалентная цепь
Допустим, что параллельно ключу S₂включается ключ S₃ с надежностью R,замыкающий цепь, когда замыкали цепь и ключ S₂. Теперь система будет функционировать нормально, если функционируют нормально ключи S₂или S₃или оба вместе.

Надежность комбинаций ключей S₂и S₃

R(S₂ + S₃) = R(S₂) + R(S₃) ‑ R(S₂)R(S₃) = 2R ‑ R².

Таким образом, надежность всей системы

R[S₁(S₂ + S₃)] = R(2 ‑ R).

Поскольку всегда R< 1, то при добавлении третьего ключа надежность системы повышается. Дополнительный ключ является резервным, так как от него не зависит работа системы.

Как показал приведенный пример, при разработке систем и анализе их надежности весьма удобно применять логические символические обозначения. Рассмотрим сложную цепь, показанную на рис. 32, б.

Эта цепь окажется замкнутой и будет проводить ток в том случае, когда истинно следующее выражение:

А + (A + BC){α + [B(C + b)]}.

Это функция вида А + f(A, В, С). Легко показать, что логи­ческую функцию вида f(x_l, x₂, ..., х_п) можно разложить и записать как

f{x₁, х₂, ..., х_п) = x₁f (I, х₂, x₃, ..., х_п) + х₁f (φ, х₂, х₃, ..., х_п),

где Iи φ – соответственно универсальное и нулевое множества. Цепи I обозначают всегда замкнуто, а φ – всегда разомк­нуто. Вместо х₁в функции f (I, х₂, ..., х_п) стоит I, а в функции f (φ, х₂, ..., х_п) – величина φ. Применив это разложение к записанной выше функции, получим

(A + BC)[α + B(C + b)] =

А(I + ВС)[φ + В(С + b)] + α(φ + ВС)[I + В(С + b)] =

= А(I + ВС)[В(С + b)] + α(ВС)[I + В(С + b)] =

АВ(С + b) + АВСВ(C + b) + αВС + αВСВ(С + b) = ВС.

Прибавив к полученному результату значение А, получим выражение для эквивалентной цепи (А + ВС). Схематически эквивалентная цепь показана на рис. 32, в.

Введение в систему резервирования повышает ее стоимость и часто сказывается на других ее параметрах, например на массе или размерах. В любой конкретной конструкции ценность дополнительной надежности должна сопоставляться с суммой соответствующих дополнительных затрат, дополнительной массой и т. д. Исследования такого рода называют оптимизацией качестваконструкции. Чаще всего это просто вопрос минимизации общих затрат. Резервирование как один из конструктивных способов повышения надежности увеличивает начальные затраты, но снижает стоимость эксплуатации. Разумеется, в ряде случаев, например при создании пилотируемых космических аппаратов, могут играть роль не экономические, а другие соображения.