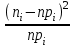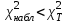АТП-121_Филимонов-лабораторная2. Ст гр. Атп121 Филимонов И. М
 Скачать 256.47 Kb. Скачать 256.47 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный технический университет» Кафедра «Прикладная математика» Семестровая работа по дисциплине «Математика специальные главы» Вариант № 5 Выполнил: ст. гр. АТП-121 Филимонов И.М. Проверил: ст. пр. каф. ПМ Арыканцев В.В. Волгоград, 2022 г. Задание 1. В таблице приведены наблюдаемые значения некоторой величины X. Требуется: 1) определить следующие числовые характеристики выборки: объем выборки, её размах, моду, медиану, среднее, дисперсию, среднее квадратическое отклонение выборки, несмещённую оценку дисперсии и среднего квадратического отклонения генеральной совокупности; 2) представить выборку в виде вариационного и статистического рядов; 3) построить полигон частот статистического ряда; 4) cоставить интервальный статистический ряд распределения частот наблюдаемых значений случайной величины Х (выбрать n = 10 интервалов одинаковой длины); 5) вычислить числовые характеристики интервального статистического ряда: объём выборки n, среднее x , дисперсию D, среднее квадратическое отклонение σ, коэффициенты асимметрии и эксцесса A и E; 6) предполагая, что исследуемая случайная величина X распределена по нормальному закону, найти теоретические частоты нормального закона распределения, проверить гипотезу о согласии эмпирической функции распределения с нормальным законом с помощью критерия согласия 2 при уровне значимости α = 0,05; 7) построить на одной диаграмме гистограмму наблюдаемых и полигон теоретических частот. Задание выполнить в табличном процессоре Microsoft Excel. Решение Вариантами называются наблюдаемые значения случайной величины, приведённые в выборке. Объёмом выборки n называется количество содержащихся в ней вариант. Вычисление объёма выборки осуществляется функцией СЧЁТ (см. рис. 1).  Рис. 1. Вычисление объёма выборки Размахом выборки называется разность между наибольшей (вычисляется функцией МАКС (см. рис. 2)) и наименьшей (вычисляется функцией МИН (см. рис. 3)) её вариантами (см. рис. 4). 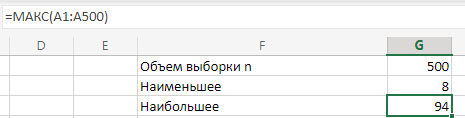 Рис. 2. Вычисление максимума 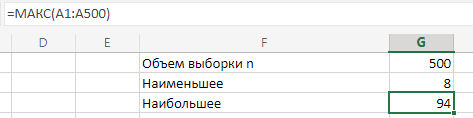 Рис.3. Вычисление минимума 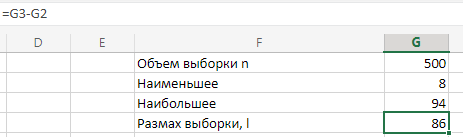 Рис. 4. Размах выборки Модой дискретного распределения называется наиболее часто встречающаяся (имеющая наибольшую частоту) варианта. Вычисление моды осуществляется функцией МОДА.НСК (см. рис. 5). 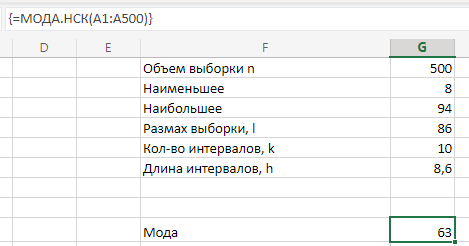 Рис. 5 Вычисление «МОДА» Медианой называется варианта, находящаяся в середине вариационного ряда. В Excel эта величина вычисляется функцией МЕДИАНА (см. рис. 6). 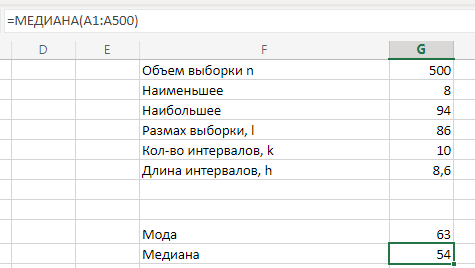 Рис. 6. Вычисляем функцию «МЕДИАНА» Среднее определяется как число, равное сумме всех чисел множества, делённой на их количество (вычисляется функцией СРЗНАЧ (см. рис. 7)). 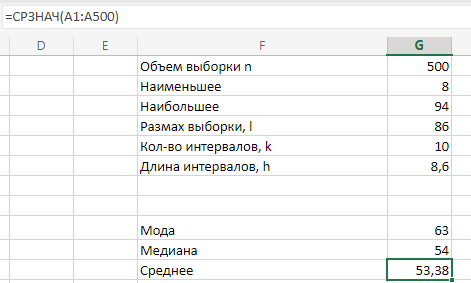 Рис. 7. Среднее значение Дисперсией называют меру разброса значений случайной величины относительно её математического ожидания (вычисляется функцией Дисп.Г (см. рис. 8)). 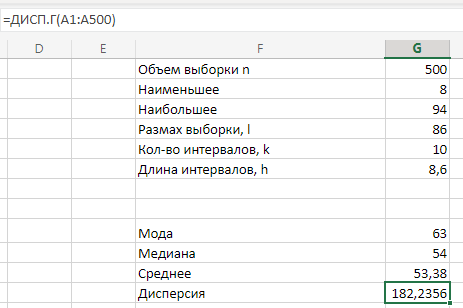 Рис. 8. Вычисляем функцию «Дисп.Г» Среднеквадратическое отклонение — наиболее распространённый показатель рассеивания значений случайной величины (вычисляется функцией СТАНДОТКЛОН.Г (см. рис. 9). 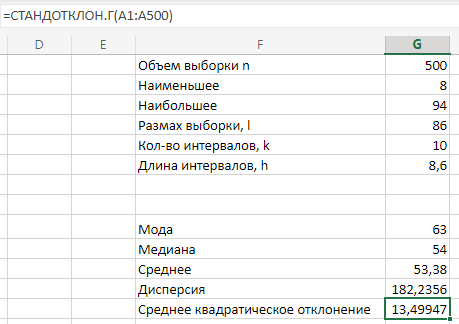 Рис. 9. Среднее квадратичное Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия (вычисляется функцией Дисп.В (см. рис. 10)). 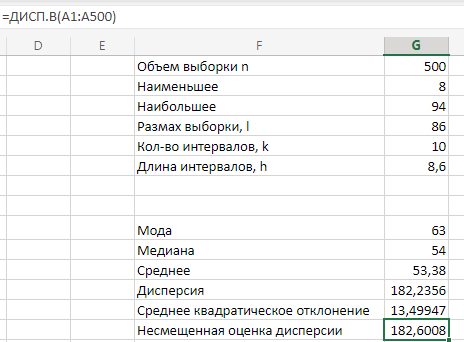 Рис. 10. Несмещенная оценка дисперсии Несмещённая оценка среднего квадратического отклонения это мера того, насколько широко разбросаны точки данных относительно их среднего(вычисляется функцией СТАНДОТКЛОН.В (см. рис. 11)). 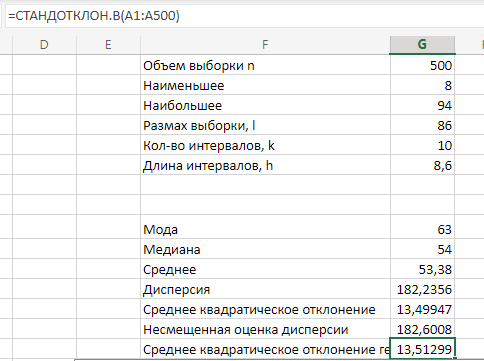 Рис. 11. Среднее квадратическое отклонение 2)Вариационным рядомназывается последовательность вариант, расположенных в возрастающем порядке. Для получения вариационного ряда в Excel нам следует расположить значения, размещённые на рабочем листе в виде массива данных в один столбец и упорядочить этот столбец по возрастанию. Создавать вариационный ряд будем на новом листе рабочей книги (добавив его при необходимости). Назовём его «Вариационный ряд». Введём в ячейку А1 нового рабочего листа в качестве названия столбца слово Данные и ввернемся на лист с исходным массивом. Для получения вариационного ряда в столбце данных, полученном при помощи буфера обмена нам достаточно отсортировать столбец данных при помощи команды Excel Сортировка по возрастанию (Главная — Редактирование — Сортировка и фильтр (см. рис. 12)).  Рис. 12. Фильтрация Для создания в Excel статистического ряда на основе вариационного мы должны выполнить следующие. При помощи команды Excel Данные — Сортировка и фильтр —Дополнительно, и в появившемся диалоговом окне расширенный фильтр установить параметры. Вычислить частоты вариант статистического ряда. Это выполняется при помощи функции массива ЧАСТОТА (см. рис. 13) 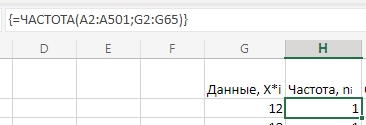 Рис. 13. Вычисление функции «Частота» Приступим к вычислению относительных частот, накопленных частот, накопленных относительных частот. Вычисления выполним в столбцах I:K, причём в столбцах I и K мы используем формулы массива (запись 'Исходные данные'!$G$1 в знаменателе обеих формул означает ссылку на ячейку G1 листа 'Исходные данные'. В которой мы вычислили объём выборки, а в столбце J, начиная с ячейки J2, создаём последовательность формул (см. рис. 14). 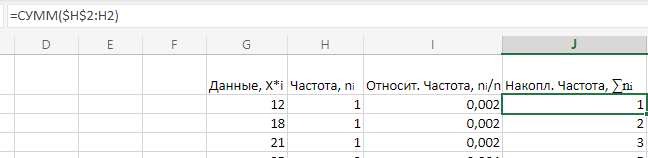 Рис. 14. Вычисление объема выборки Полигоном частот статистического ряда называется ломаная, соединяющая точки. Для построения полигона частот выделим диапазон G1:H65, на вкладке ленты Вставка, группа Диаграмма выберем Точечная с прямыми отрезками и маркерами. На рис. 15 приведено изображение полигона частот статистического ряда 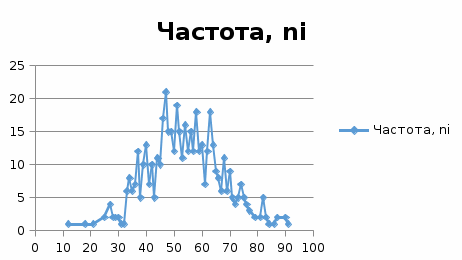 Рис. 15. Полигон частот статистического ряда 4)Представим теперь исходные данные в виде группированного статистического ряда с интервалами равной длины. Для заданного количества интервалов k= 10 и вычисленного ранее размаха выборки вычислим h— длину интервала. 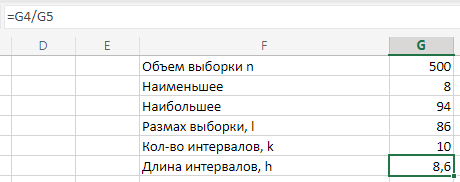 Рис. 16. Длина интервалов В столбцах A и C формулы создаются как последовательность формул (см. рис. 17), начиная с третьей строки рабочего листа, середины интервалов в столбце D и частота в столбце E вычисляются как формула массива. На рис. 18 приведён результат вычислений. 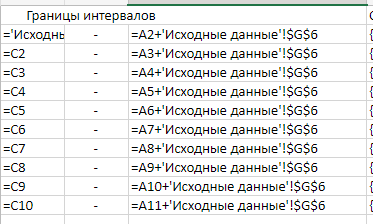 Рис. 17. Формулы вычислений 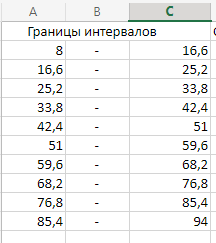 Рис. 18. Результат вычислений Вычисление относительных частот, накопленных частот и накопленных относительных частот группированного статистического ряда аналогично вычислениям «простого» статистического ряда. Вычисление объёма выборки осуществляется функцией СЧЁТ (см. рис. 19). 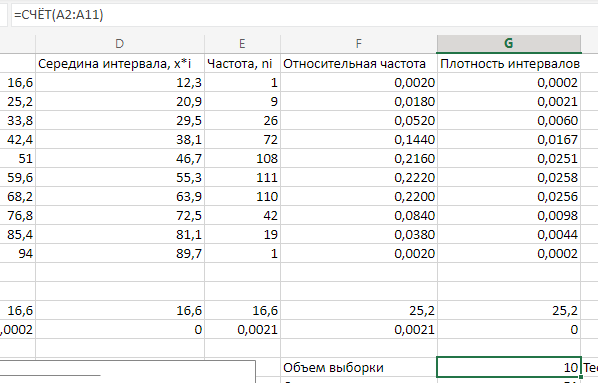 Рис. 19. Осуществление функции «СЧЁТ» Среднее определяется как число, равное сумме всех чисел множества, делённой на их количество (вычисляется функцией СРЗНАЧ (см. рис. 20)).  Рис. 20. Вычисление среднего значения Дисперсией называют меру разброса значений случайной величины относительно её математического ожидания (вычисляется функцией Дисп.Г (см. рис. 21)). Среднеквадратическое отклонение — наиболее распространённый показатель рассеивания значений случайной величины (вычисляется функцией КОРЕНЬ от Дисперсии (см. рис. 21)). Вычисление асимметрии и эксцесса должны быть введены как формулы массива.(см. рис. 21) 6)Исходя из вида гистограммы частот группированного статистического ряда (см. рис. 19), выдвинем гипотезу о нормальном распре- делении рассматриваемой случайной величины Аргументы x, среднее, стандартное_откл определяют: значение x, для которого вычисляется функция и параметры aи s— параметры нормального закона распределения соответственно; аргумент интегральная — логический: ИСТИНА — функция Excel возвращает значение интегральной функции распределения; ЛОЖЬ — функция Excel возвращает значение дифференциальной функции распределения. Критерий согласия (теоретический) в Excel вычисляется при помощи функции ХИ2.ОБР Вычислим значения массива в ячейках I18:I27 по формуле (1) и сумму этих значений критерия согласия (наблюдаемый) (см. рис. 21) 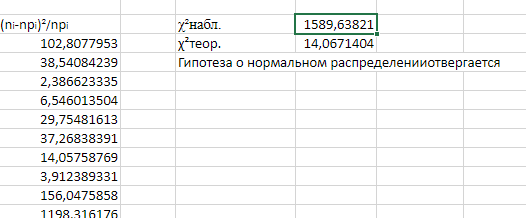 Рис.21. Значения массива в ячейках
Если
гипотеза о характере распределения принимается и отвергается в противном случае. 7) на Рис. 22 — результаты вычислений и гистограмма наблюдаемых и полигон теоретических частот 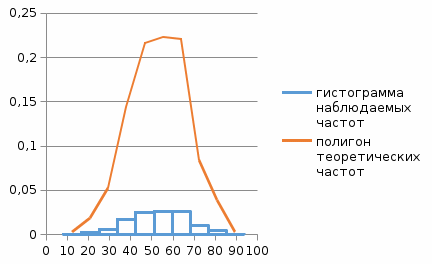 Рис. 22. Гистограмма наблюдаемых и полигон теоретических частот |