Курсовая работа. Статистический анализ показателей комплексной диагностики сердечнососудистых заболеваний

• Название: Статистический анализ показателей комплексной диагностики сердечнососудистых заболеваний
• Дата: 25.02.2018
• Размер: 0.92 Mb.
• Имя файла: Курсовая работа.docx
• Тип: Пояснительная записка; #37188
• страница: 7 из 8

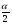, K) и находим t_крит = 2,3.
Таблица 44 – Критерий Стьюдента

Критерий Стьюдента
Хср1	Хср2	tрасч	K	tкр
74,03333	125,3333	-46,4	58	2,301084

Так как t_расч < t_крит, то гипотеза о равенстве средних значении выборок не принимается. Следовательно, отвергается и нулевая гипотеза, что говорит о разных статистических свойствах данных выборок.

Непараметрический U-критерий Уилкоксона (Манна-Уитни) проверяет гипотезу о равенстве средних двух независимых выборок. Рассчитаем параметры U₁ и U₂ по формулам (23) и (24) соответственно. Как видно из этих формул, нужно рассчитать R₁ и R₂, а затем подсчитать их сумму. Для этого два столбца данных, которые мы анализируем, копируем в один, и при помощи фильтра располагаем в возрастающем порядке. Напротив каждого значения из массива данных вписываем его порядковый номер. И теперь подсчитываем сумму этих порядковых номеров, при помощи соответствующей функции программы Excel.

R₁ = 2221, что соответствует сумме порядковых номеров данных, приведенных для значений частоты сердечных сокращений в норме. R₂ = 3760, что соответствует сумме порядковых номеров данных для значений частоты сердечных сокращений при синусовой тахикардии.

Подставляем эти значения в формулы 23 и 24 соответственно, и получаем, что U₁ = -856, а U₂ = -2395.

Критическое значение U_крит определяют по статистическим таблицам. У нас U_крит = -8396,76. В нашем случае U_расч > U_крит.
Таблица 45 – U-критерий Уилкоксона

U - критерий Уилкоксона
U1	U2	Uрасч	Uкр	R1	R2
-856	-2395	-2395	-8396,76	2221	3760

Так как U_расч > U_кр, то нулевая гипотеза отвергается, и статистические характеристики двух выборок неодинаковы. На основании того, что в большинстве случаев нулевая гипотеза подтвердилась, можно судить о том, что статистические характеристики выборок совпадают.

Затем определяется W-критерий Уилкоксона для проверки равенства средних двух независимых выборок. Две выборки снова объединяются в одну, ранжируются, а затем рассчитываются суммы рангов, соответствующие обеим выборкам ∑R₁ и ∑R_2. W_расч определяется как наименьшая сумма рангов. По формулам (25) и (27) вычисляются верхнее W(Q, n_1, n₂) и нижнее значения статистики w(Q, n_1, n₂). Результаты вычислений показаны в таблице 46.

Таблица 46 – W-критерий Уилкоксона

W - критерий Уилкоксона
Wрасч	Q	Ψ	w	W
3760	0,1	1,281552	903,2396	926,7604

Получается, что W_расч > w(Q, n_1, n₂), значит, нулевая гипотеза об одинаковом распределении обеих выборок принимается на уровне значимости Q.


2.6 Корреляционный анализ

Вычисляем корреляцию по формуле (28). Для этого на отдельный лист выносим столбцы и группируем их следующим образом:

• 
  Для патологии: синусовая тахикардия и пароксизмальная тахикардия, фибрилляция желудочков и синусовая тахикардия, пароксизмальная тахикардия и фибрилляция желудочков.
  
• 
  Для нормы: умеренные нагрузки и высокие нагрузки, частота сердечных сокращений и умеренные нагрузки, высокие нагрузки и частота сердечных сокращений в покое.
  

Один из этих столбцов именуем Х, другой Y. Далее следуя формуле 28 находим сумму каждого их этих столбцов. Дополнительно для данного расчета высчитываем сумму всех значений Х, возведенную в квадрат и сумму всех значений Y, также возведенную во вторую степень. Высчитываем шесть коэффициентов корреляции.

Результаты вычислений представлены в таблице 47.
Таблица 47 – Коэффициенты корреляции

Коэффициенты корреляции
r (X2;X3)	0,253547115
r(X1;X2)	0,126312411
r(X1;X3)	0,035464162
r (X2;X3)	-0,141869743
r(X1;X2)	-0,119826693
r(X1;X3)	-0,00688149

Строим лепестковую диаграмму по шести полученным значениям.

Рисунок 31 – Лепестковая диаграмма
По полученным данным и данной диаграмме можно судить о непрямой и слабой зависимости признаков Х_{1 ,} Х₂ ,Х₃ относительно друг друга, поскольку коэффициент корреляции меньше 1.