Курсовая работа. Статистический анализ показателей комплексной диагностики сердечнососудистых заболеваний
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
Статистический анализ данных1.2.1 Проведение статистического анализа исследуемых данныхОбработка начинается с систематизации или упорядочивания данных. Этот процесс называется группировкой. Среди группировок особое место занимают вариационные ряды. К ним относится двойной ряд чисел, показывающий, каким образом связаны с их повторяемостью в данной статистической совокупности. В зависимости от того, как варьируют признаки – дискретно или непрерывно – статистическая совокупность разделяется в безынтервальный или интервальный вариационные ряды. Для того, чтобы подсчеты были более точными данные можно разбить на группы или классы. Эту задачу решают делением размаха варьирования признака на число групп или классов, намечаемых при построении вариационного ряда. Величину классового интервала устанавливают по формуле: 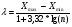 , (1) , (1)где: - λ – величина классового интервала; - Xmax – максимальная варианта совокупности; - Xmin – минимальная варианта совокупности; - n – число наблюдений. В ходе построения вариационного ряда следует поступать так, чтобы минимальная варианта совокупности попадала примерно в середину первого классового интервала. Этому требованию удовлетворяет формула 2: 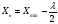 , (2) , (2)где: - Хн – нижняя граница первого классового интервала. Последовательно добавляя к Хн λ, разбиваем ряд на классовые интервалы. Путем уменьшения верхних границ на величину, равную точно сти, принятой при измерении признака, достигается необходимое разграничение классов. Затем следует заменить классовые интервалы на их центральные значения. Для этого используется формула: 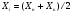 , (3) , (3)где: – Хк – конечная точка интервала. После проведенных расчетов приступаем к вычислениям статистических показателей. Дисперсия рассчитывается по формуле: 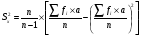 (4) (4)Индекс X у символа дисперсии обозначает, что этот показатель характеризует варьирование числовых значений признака вокруг их средней арифметической, она измеряет и внутреннюю изменчивость значений признака, зависящую от разностей между наблюдениями. Преимущество дисперсии перед другими показателями вариации со стоит также и в том, что она разлагается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на ве личину учитываемого признака. Среднее квадратическое отклонение - показатель, представляющий квадратный корень из дисперсии: 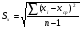 (5) (5)Показатель вариации представляет собой среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической: 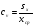 (6) (6)Вариационные ряды и их графики дают наглядное представление о варьировании признаков, но они недостаточны для полного описа ния варьирующих объектов. Для этой цели служат особые, логически и теоретически обоснованные числовые показатели, называемые статистическими характеристиками. К ним относятся, прежде всего, средние величины и показатели вариации. Значение средних чисел заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отли чать один групповой объект от другого. Из общего семейства степенных средних наиболее часто исполь зуют среднюю арифметическую. Этот показатель является центром распределения, вокруг которого группируются все варианты стати стической совокупности. Средняя арифметическая может быть про стой и взвешенной. Простую среднюю арифметическую определяют, как сумму всех членов совокупности, деленную на их общее число: 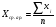 , (7) , (7)где: - Хi – сумма всех членов совокупности; - n – общее число вариант. Мода – это величина, наиболее часто встречающаяся в данной совокупности (для безынтервального ряда): 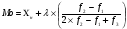 , (8) , (8)где: - Xн – нижняя граница модального класса; - λ – величина классового интервала; - f2 – частота модального класса; - f1 – частота класса, предшествующего модальному; - f3 – частота класса, следующего за модальным. Для придания большей наглядности результатам статистических исследований проводят построение графиков. При построении графика безинтервального вариационного ряда по оси абсцисс откладывают срединные значения классов, по оси ординат - частоты. Высота перпендикуля ров, восставляемых по оси абсцисс, соответствует частотам классов. Соединяя вершины перпендикуляров прямыми линиями, получают геометрическую фигуру в виде многоугольника, называемую полигоном распределения частот. Линия, соединяющая вершины перпен дикуляров, называется вариационной кривой или кривой распределе ния частот вариационного ряда. При построении графика интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов, по оси ор динат - частоты интервалов. В результате получается так называемая гистограмма распределения частот. Если по оси абсцисс откладывать значения классов, а по оси ор динат - накопленные частоты с последующим соединением точек прямыми линиями, получается график, называемый кумулятой. В отличие от вариационной кривой, имеющей ку полообразную форму, кумулята имеет вид S-образной кривой. Нако пленные частоты находят последовательным суммированием частот в направлении от первого класса до конца вариацион ного ряда. Откладывая по оси абсцисс кумулированные частоты, а по оси ординат - значения классов с последующим соединением геометри ческих точек прямыми линиями, получают линейный график, назы ваемый огивой. Медиана - средняя величина, относительно которой ряд распре деления делится на две равные части: в обе стороны от медианы рас полагается равное число вариант. Для данных, сгруппированных в вариационный ряд, медиана оп ределяется следующим образом. Сначала находят класс, содержащий медиану. Для этого частоты ряда кумулируют от меньших к большим значениям класса до ве личины, большей половины всех членов данной совокупности. 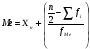 , (9) , (9)где: - Xн – нижняя граница модального класса; - ∑fi – сумма накопленных частот, соответствует классу, предшествующему медиальному; - n – общее число наблюдений; - fMe – частота класса, содержащего медиану. Квантили- структурная характеристика вариационного ряда, от секающая в пределах ряда определенную часть его членов. К квантилям относятся квадратили, децили ипроцентили. 99процентилей делят ряд на 100 равных частей. Сами процентили находят по формуле 10: 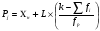 , (10) , (10)где: – Xн – нижняя граница класса, содержащего процентиль; – fp – частота класса, содержащего искомый процентиль; – L – величина интервального класса. 1.2.2 Законы распределения Закон нормального распределения (нормальный закон) выражает функциональную зависимость между вероятностью P(x) и нормированным отклонением t. Нормированное отклонение - это отклонение той или иной варианты от средней арифметической, отнесенное к величине среднего квадратического отклонения. Этот показатель позволяет «измерять» отклонения отдельных вариант от среднего уровня и сравнивать их для разных признаков. Функция f(x), связывающая значения хi переменной случайной величины х с их вероятностями Pi, называется законом распределения этой величины. Закон распределения случайной величины можно задать таблично, выразить графически в виде кривой вероятности и описать соответствующей формулой. Для нормального распределения применяется формула: 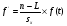 , (11) , (11)где: - f’ – теоретические частоты вариационного ряда; - f(t) – значения функции нормированного отклонения. Равномерный закон распределения описывается формулой: 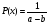 (12) (12)При распределении Максвелла используется следующая формула: 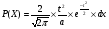 (13) (13)Среди асимметричных распределений встречаются такие, которые неплохо описывает формула Шарлье. Однако эту формулу имеет смысл применять в тех случаях, когда эмпирическое распределение обнаруживает эксцесс: 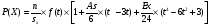 , (14) , (14)где: - As - асимметрия; - Ex – эксцесс. Среди эмпирических распределений асимметрия и эксцессвстречаются довольно часто. Заметить их можно по характеру рас пределения частот в классах вариационного ряда. Графически асим метрия выражается в скошенной вариационной кривой, вершина ко торой может находиться левее или правее центра распределения. В первом случае асимметрия называется правостороннейили поло жительной, а во втором - левостороннейили отрицательной(по знаку числовой характеристики). Островершинность кривой распределения вызывается чрезмер ным накапливанием частот в центральных классах вариационного ряда, из-за чего вершина кривой распределения оказывается сильно поднятой вверх. В таких случаях говорят о положительном эксцессе распределения. Кроме того, встречаются многовершинные и плоско вершинные кривые, что свидетельствует о наличии у такого распре деления отрицательного эксцесса. Асимметрию и эксцесс можно вычислить метод условной средней. Для этого из класса с наибольшей частотой берётся среднее значение и обозначатся через А. Находят поправку, которую необходимо прибавить или вычесть от условной средней, чтобы получить значения средней арифметической. Такой поправкой служит условный момент первого порядка, и находится он по формуле: 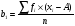 (15) (15)Так же для дальнейших расчетов находятся условные моменты второго, третьего и четвертого порядков (соответственно b2, b3, b4): 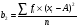 ; ; 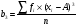 ; ;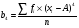 Они необходимы для расчета центральных моментов третьего и четвертого порядка, которые лежат в основе формул по нахождению асимметрии (As) и эксцесса (Ex). Собственно, центральные моменты находятся следующим образом: 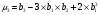 , (16) , (16)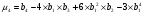 (17) (17)Асимметрия находится по формуле: 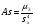 (18) (18)Эксцесс находится с помощью формулы: 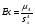 (19) (19)1.2.3 Параметрические и непараметрические критерии Проверку адекватности данных двух выбранных столбцов значений проводят помощью параметрических и непараметрических критериев. Проверка адекватности данных производится по нулевой гипотезе. Сущность ее сводится к предположению, что разница между генеральными параметрами сравниваемых групп равна нулю и что различия, наблюдаемые между выборочными характеристиками, носят не систематический, а исключительно случайный характер. Для проверки нулевой гипотезы используют параметрические и не параметрические критерии. Параметрические: Критерий Фишера (F-критерий) используется для определе ния равенства дисперсий (D) двух независимых (в том числе мало численных) выборок. Примем нулевую гипотезу - дисперсии выборок равны. Рассчитываем дисперсию по формуле: 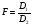 (20) (20)Далее при использовании функции FРАСПОБР находится Fкрит. И если Fкрит> Fрасч, то гипотеза принимается. Для определения критического коэффициента вычислим число степеней свободы (К). Будем использовать следующую формулу: 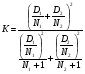 (21) (21)Критерий Стьюдента (t-критерий) используется для провер ки равенства средних значений двух нормально распределенных не зависимых выборок. 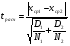 (22) (22)Далее вычисляется критическое значение t-критерия с помощью функции СТЬЮДРАСПОБР. Если tкрит> tрасч, то гипотеза принимается. Если дисперсии выборок не равны, то вычислим средние значения и дисперсии выборок, используя функции СРЗНАЧ, ДИСП. Непараметрические: U-критерий Уилкоксона (Манна-Уитни) проверяет гипотезу о равенстве средних двух независимых выборок.Дисперсии выборок равны. Самый строгий непараметрический критерий. Нулевая гипотеза. Две независимые выборки принадлежат к од ной и той же генеральной совокупности или к совокупностям с оди наковыми параметрами. Их функции распределения равны. Равны средние и медианы. Рассчитываем параметры U1 и U2 по формулам: 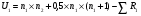 , (23) , (23)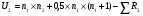 . (24) . (24)Критическое значение статистики можно найти в специаль ных таблицах или вычислить через критическое значение статистики. W-критерий Уилкоксона: Две выборки объединяем в одну, ранжируем ее, а затем рассчитываем суммы рангов, соответствующие обеим выборкам ∑R1 и ∑R2. Вычисленное значение Wрасч, сравниваем с верхним W(Q, n1, n2) и нижним w(Q, n1, n2) критическими значениями статистики. Найдем нижнее критическое значение статистики: 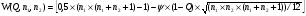 , (25) , (25)где: – Q – уровень значимости для одностороннего критерия; – Ψ – значение функции, обратной стандартному. В формуле появляются новые обозначения: Q и, поэтому находим сначала их: 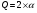 (26) (26)Теперь вычисляем верхнее значение статистики, связанное с нижним соотношением по формуле: 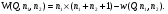 (27) (27)1.2.4 Корреляция признаков Для описания связей между переменными величинами применяют математическое понятие функции f, которая ставит в соответствие каждому определенному значению независимой переменной X, называемой аргументом, определенное значение зависимой переменной Y: y=f(x). Здесь x – аргумент, а y- соответствующее ему значение функции f(x). Такого рода однозначные зависимости между переменными величинами Y и X называют функциональными. Наряду с анализом двумерных совокупностей в биологии широкое применение находит статистический анализ многомерных корреляционных связей. Простейшим случаем множественной корреляции является зависимость между тремя величинами. Корреляционная связь между признаками бывает линейной и нелинейной, положительной и отрицательной. Задача корреляционного анализа сводится к установлению направления и формы связи между варьирующими признаками, измерению ее тесноты и, наконец, к проверке достоверности выборочных показателей корреляции. Сопряженность между переменными величинами Y и X можно установить, сопоставляя числовые значения одной из них с соответствующими значениями другой. Если при увеличении одной переменной увеличивается другая, это указывает на положительную связь между этими величинами, и, наоборот, когда увеличение одной переменной сопровождается уменьшением значений другой, это указывает на отрицательную связь. Иная ситуация наблюдается в случае варьирующих признаков. Здесь приходится исследовать собственно не приращение или уменьшение функции, а сопряженную вариацию (ковариацию), выражая ее в виде взаимно связанных отклонений вариант от их средних y и x. Ее измеряют с помощью коэффициента множественной корреляции: 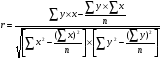 (28) (28)Коэффициент корреляции - отвлеченное число, лежащее в пределах от -1 до +1. При независимом варьировании признаков, когда связь между ними полностью отсутствует, r = 0. Чем сильнее сопряженность между признаками, тем выше значение коэффициента корреляции. Следовательно, при |r| > 0 этот показатель характеризует не только наличие, но и степень сопряженности между признаками. При положительной или прямой связи, когда большим значениям одного признака соответствуют большие же значения другого, коэффициент корреляции имеет положительный знак и находится в пределах от 0 до +1, при отрицательной или обратной связи, когда большим значениям одного признака соответствуют меньшие значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до -1. |
