Ответы к зачету по Деревянным конструкциям. Структура древесины, её влияние на прочность и деформативность материала

• Название: Структура древесины, её влияние на прочность и деформативность материала
• Анкор: Ответы к зачету по Деревянным конструкциям
• Дата: 02.05.2022
• Размер: 5.2 Mb.
• Имя файла: Otvety_k_zachetu_po_DK (1).docx
• Тип: Документы; #507197
• страница: 2 из 5

Центральное сжатие древесины

Расчет центрального сжатия древесины, расчет на прочность центрально сжатых стержней производится с учетом ослаблений сечения. Опыты показывают, что концентрация напряжений у мест ослаблений при сжатии значительно менее снижает прочность, чем при растяжении. Это объясняется более пластичной работой древесины при сжатии.

Расчет производится по формуле (2):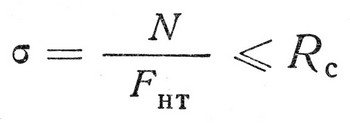



где N — расчетная сжимающая сила;

      R_c — расчетное сопротивление сжатию.

 

Сжатые стержни, имеющие более или менее значительную длину и не закрепленные в поперечном направлении, рассчитываются на прочность и на продольный изгиб.

7. Работа элементов цельного сечения из дерева на изгиб. Расчет элементов цельного сечения из древесины на изгиб.

В изгибаемых элементах от нагрузок, действующих поперек продольной оси, возникают изгибающие моменты М и поперечные силы Q, определяемые методами строительной механики. Например, в однопролетной балке пролетом l от равномерно-распределенной нагрузки q возникают изгибающие моменты   и поперечные силы  .

От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба σ, которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается.

Диаграмма как и для сжатия, примерно до половины, имеет линейное очертание, затем изгибается, показывая ускоренный рост прогибов.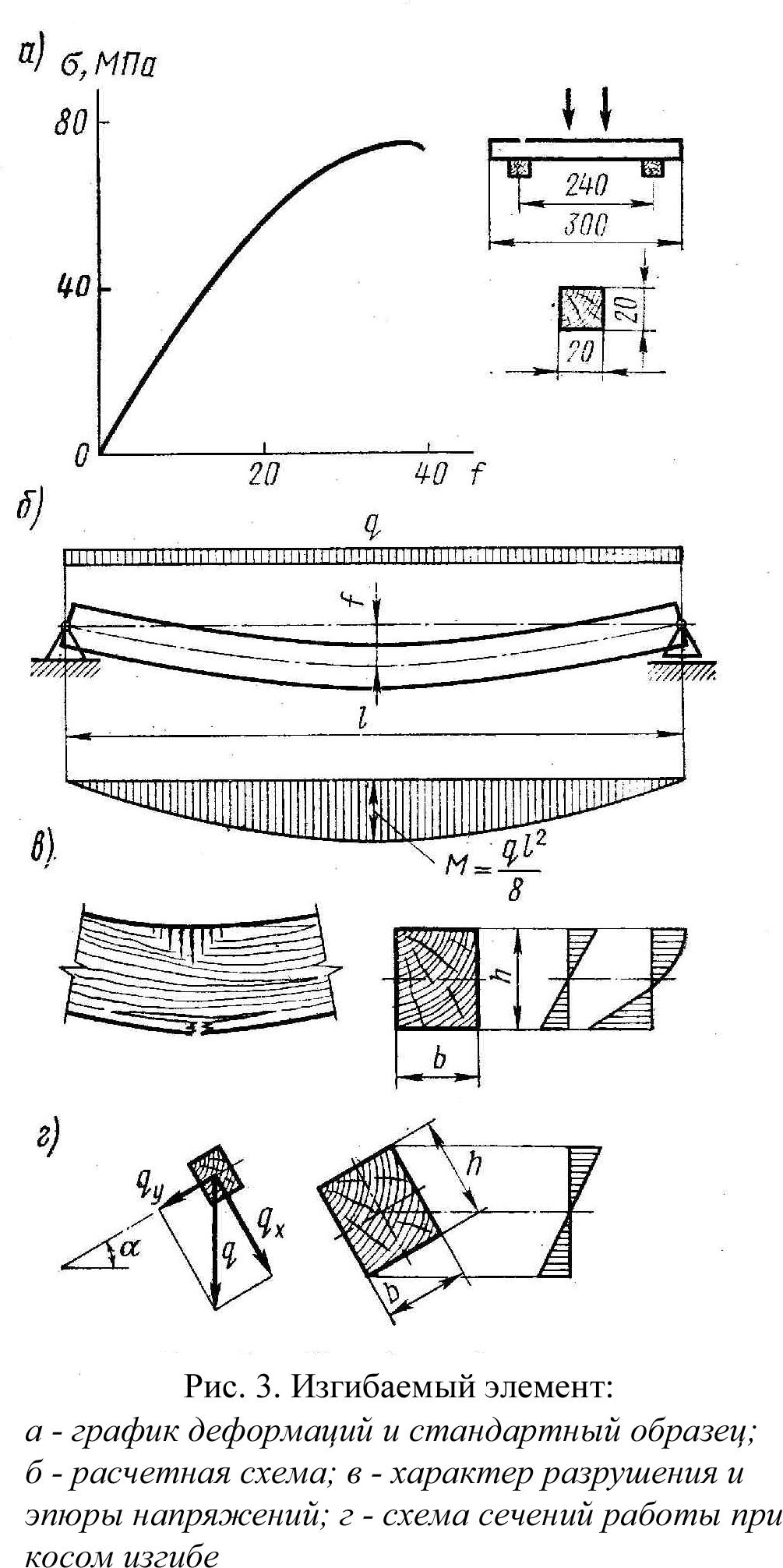

=80 МПа – предел прочности чистой древесины на изгиб при кратковременных испытаниях. Разрушение образца начинается с появления складок в крайних сжатых волокнах и завершается разрывом крайних растянутых. Расчетное сопротивление изгибу по СНиП II-25-80 рекомендуется принимать таким же, как и при сжатии, т.е. для 1 сорта R_и=14 МПа – для элементов прямоугольного сечения высотой до 50 см. Брусья с размерами сечения 11 – 13 см. при высоте сечения 11 – 50 см. имеют меньше перерезанных волокон при распиловке, чем доски, поэтому их прочность повышается до R_и=15 МПа. Бревна шириной свыше13 см. при высоте сечения 13 – 50 см. совсем не имеют перерезанных волокон, поэтому R_и=16 МПа.



Расчет изгибаемых элементов на прочность

Производится по формуле:

σ= , где

М – максимальный изгибающий момент,

W_расч – расчетный момент сопротивления поперечного сечения.

Для наиболее распространенного прямоугольного сечения

;  .

Подбор сечения изгибаемых элементов производится по этой же формуле, определяя  , затем, задавая один из размеров сечения (b или h), находят другой размер.

Расчет на устойчивость поской формы дефорирования элементов прямоугольного постоянного сечения

Производят по формуле:

σ= , где

М – максимальный изгибающий момент на рассматриваемом участке l_p,

W_бр – максимальный момент сопротивления брутто на рассматриваемом участке l_p,

φ_м – коэффициент устойчивости.

Коэффициент φ_м для изгибаемых элементов прямоугольного постоянного поперечного сечения шарнирно-закрепленных от смещения из плоскости изгиба, следует определять по формуле:

,где

l_p – расстояние между опорными сечениями элемента (расстояние между точками закрепления сжатого пояса),

b – ширина поперечного сечения,

h – максимальная высота поперечного сечения на участке l_p,

k_ф – коэффициент, зависящий от формы эпюры на участке l_p (определяется по таблице СНиП II-25-80).

При расчете элементов переменной высоты сечения значение коэффициента φ_м следует умножать на коэффициент k_жм, а при подкреплении из плоскости изгиба в промежуточных точках растянутой кромки – на коэффициент k_пм.

Оба эти коэффициента определяются по СНиП.

При наличии точек закрепления растянутых зон n≥4, k_жм=1.

Проверку устойчивости плоской формы изгиба элементов постоянного двутаврового или коробчатого сечения следует производить в тех случаях, когда l_p≥7b, где b – ширина сжатого пояса поперечного сечения. Расчет следует производить по формуле:

, где

φ – коэффициент продольного изгиба сжатого пояса,

R_c – расчетное сопротивление сжатию,

W_бр – момент сопротивления брутто, в случае фанерных стенок – приведенный момент сопротивления в плоскости изгиба элемента.

3. Проверка на скалывание при изгибе

Выполняется по формуле Журавского:

, где

Q – расчетная поперечная сила;

I_бр – момент инерции брутто рассматриваемого сечения;

S_бр – статический момент брутто сдвигаемой части сечения относительно нейтральной оси;

b – ширина сечения;

R_ск – расчетное сопротивление скалыванию при изгибе (для древесины I сорта R_ск=1,8 МПа для неклееных элементов, R_ск=1,6 МПа – для клееных элементов вдоль волокон).

В балках прямоугольного сечения при l/h≥5 скалывания не происходит, однако оно может быть в элементах других форм сечения, например, в двутавровых балках с тонкой стенкой.

4. Проверка изгибаемых элементов по прогибам

Определяется относительный прогиб, значение которого не должно превышать предельного значения, регламентированного СНиПом:



Наибольший прогиб f шарнирно-опертых и консольных изгибаемых элементов постоянного и переменного сечения следует определять по формуле:

, где

f₀ – прогиб балки постоянного сечения без учета деформаций сдвига (например, для однопролетной балки  ;

h – наибольшая высота сечения;

k – коэффициент, учитывающий переменность высоты сечения, для балки постоянного сечения k=1;

с – коэффициент, учитывающий деформации сдвига от поперечной силы.

Значения коэффициентов k и с приведены в СНиП.

Клееные криволинейные элементы, изгибаемые моментом М, уменьшающим их кривизну, следует проверять дополнительно на радиальные растягивающие напряжения по формуле:

σ_r= , где

σ₀ – нормальные напряжения в крайнем волокне растянутой зоны.

σ_i – нормальные напряжения в промежуточном волокне сечения для которого определяются радиальные растягивающие напряжения;

h_i – расстояние между крайними и рассматриваемыми волокнами;

r_i – радиус кривизны линии, проходящей через центр тяжетси эпюры нормальных растягивающих напряжений, заключенной между крайними и рассматриваемыми волокнами.

Косой изгиб

Возникает в элементах, оси сечений которых расположены наклонно к направлению нагрузок, как например, в брусчатых прогонах скатных покрытий.

q 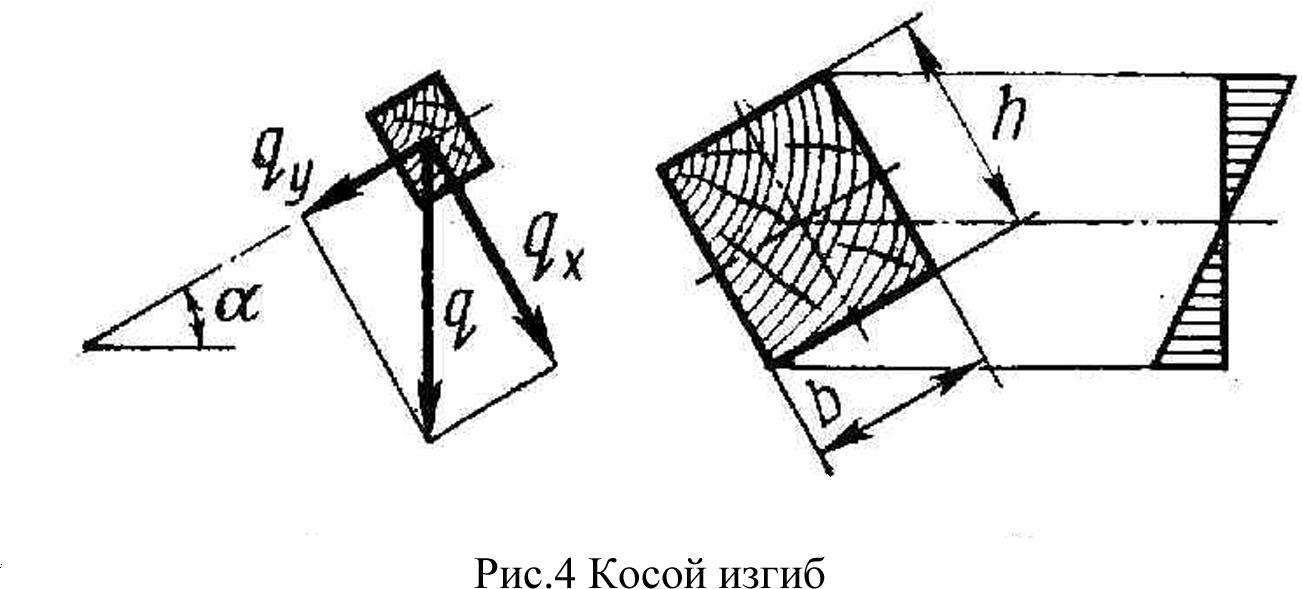_x=qsinα;

q_y=qcosα;

M_x=Msinα;

M_y=Mcosα.

Вертикальная нагрузка q и изгибающие моменты М при косом изгибе под углом α раскладываются на нормальную (q_y) и скатную (q_x) составляющие.

Проверку прочности при косом изгибе производят по формуле:

σ= .

Подбор сечений косоизгибаемых элементов производят методом попыток. Расчет по прогибам производят с учетом геометрической суммы прогибов относительно каждой из осей сечения:

.

8. Работа элементов цельного сечения из дерева на растяжение. Расчет элементов цельного сечения из древесины на растяжение.

Работа элементов цельного сечения из дерева на растяжение.

Разрушение древесины при растяжении начинается со скольжения мицелл и заканчивается разрывом волокон, зачастую сопровождающимся скалыванием на участках между отдельными волокнами (рис. II—1). Разрыв древесины происходит при малых деформациях (менее 1%) и носит хрупкий характер. На работе и прочности растянутых элементов строительной древесины очень неблагоприятно сказываются сучки, косослой, трещины и ослабления. Самое неблагоприятное влияние на прочность растянутых деревянных элементов оказывают сучки, которые не только ослабляют площадь поперечного сечения, но и, располагаясь несимметрично по отношению к продольной оси элемента, переводят работу центрально растянутых элементов в категорию пространственно внецентренно растянутых, то есть резко ухудшают условия их работы. Кроме того, возле каждого сучка более или менее развит присучковый косослой, то есть резкое и значительное отклонение волокон от своего прямого направления. Прочность же древесины на растяжение под углом к волокнам снижается в десятки раз по сравнению с прочностью вдоль волокон. Особенно неблагоприятен косослой, выходящий на кромки. Наблюдения показали, что вредное влияние ослаблений, заключающееся в концентрации напряжений, сказывается на работе растянутых деревянных элементов значительно сильнее, чем на работе металлических. Объясняется это тем, что разрушение деревянных растянутых элементов происходит почти мгновенно, площадка текучести на диаграмме растяжения древесины отсутствует. Поэтому перед разрушением растянутого деревянного элемента происходит не выравнивание напряжений в параллельно работающих волокнах, а последовательный разрыв наиболее нагруженных из них. В центрально растянутых элементах необходимо проверять прочность по площади с наибольшим ослаблением:



где N — действующее в элементе усилие;

Fнт — расчетная площадь ослабленного сечения.

При определении расчетной площади Fнт условно считают совмещенными в одном поперечном сечении все ослабления элемента, если расстояние между ними вдоль элемента не превышает 20 см. В растянутых стержнях, состоящих из нескольких элементов, следует проверить прочность каждого элемента по его наиболее ослабленному сечению. Усилия между элементами при равномерном загружении распределяются пропорционально площадям их поперечных сечений брутто. В случаях неравномерного загружения совместно работающих растянутых элементов (например, прокладки и накладки растянутых стыков на нагелях) усилие в каждом отдельном элементе определяют в зависимости от грузоподъемности прикрепляющих его связей. Подбор сечения растянутых элементов ведут в порядке, обратном проверке напряжений. Требуемую площадь определяют по формуле:



где k_ос = F:Fнт — коэффициент, учитывающий ослабление элемента.

Для предварительных расчетов величину kос можно принять равной 1,25-1,50. В отдельных случаях значение k_ос приближается к 2.

После расчета и размещения связей, прикрепляющих данный элемент, необходимо проверить напряжения по формуле (II—1) с учетом действительных ослаблений связями, примененными в конструкции.

Предел прочности древесины хвойных пород при растяжении поперек волокон весьма невелик и равен примерно 1/45 предела прочности при растяжении вдоль волокон. Пороки строительной древесины при растяжении поперек волокон сказываются еще сильнее, чем при растяжении вдоль волокон. Например, трещины (усушечные, морозобойные и др.) или прорость могут свести к нулю прочность древесины на растяжение поперек волокон. Поэтому в несущих деревянных конструкциях не следует допускать работу древесины на растяжение поперек волокон.

Расчет элементов цельного сечения из древесины на растяжение

Элементами деревянных конструкций называют доски, бруски, брусья и бревна цельного сечения с размерами, указанными в сортаментах пилёных и круглых материалов. Они могут являться самостоятельными конструкциями, например, балками или стойками, а также стержнями более сложных конструкций. Усилия в элементах определяют общими методами строительной механики. Проверка прочности и прогибов элемента заключается в определении напряжений в сечениях, которые не должны превышать расчетных сопротивлений древесины, а также его прогибов, которые не должны превосходить предельных, установленных нормами проектирования. Деревянные элементы рассчитывают в соответствии со СНиП II-25-80.

Элементы конструкций рассчитывают по методу предельных состояний. Предельным называют такое напряженное состояние конструкции, за пределами которого эксплуатация ее невозможна.

Рассматривают два вида предельных состояний:

1. по несущей способности (прочности, устойчивости);

2. по деформациям (прогибам, перемещениям).

Расчет по первому предельному состоянию производится на расчетные нагрузки, является основным и используется при подборе поперечных сечений элементов. Расчет по второму предельному состоянию производится на нормативные нагрузки.

Р 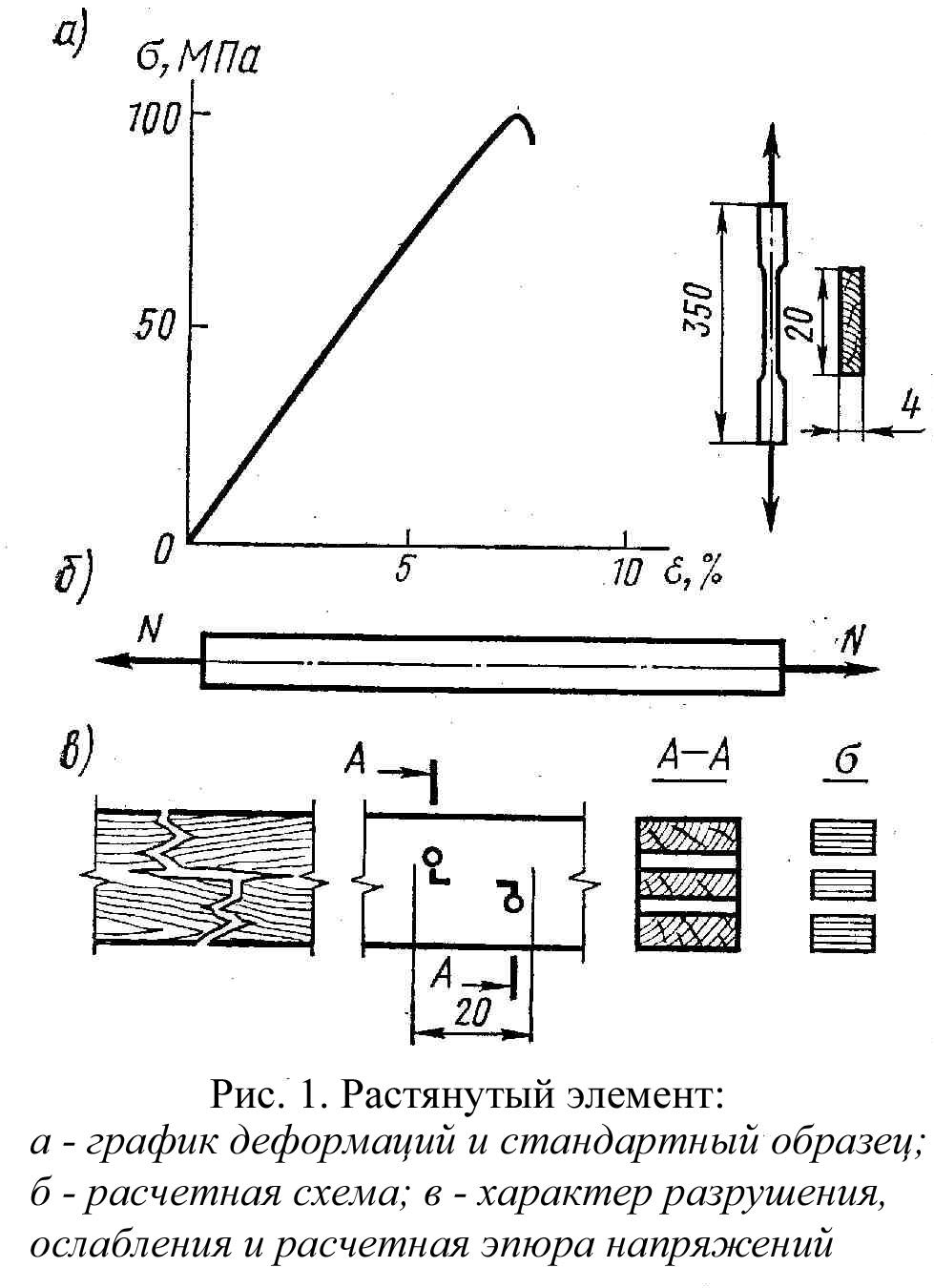астянутые элементы

На растяжение работают нижние пояса и отдельные раскосы ферм, затяжки арок и других сквозных конструкций. Растягивающее усилиеN действует вдоль оси элемента и во всех точках его поперечного сечения возникают растягивающие напряжения σ, которые с достаточной точностью считаются одинаковыми по величине.

Древесина на растяжение работает почти упруго и показывает высокую прочность. Разрушение происходит хрупко в виде почти мгновенного разрыва. Стандартные образцы при испытаниях на растяжение имеют вид «восьмерки».

Как видно из диаграммы растяжения древесины без пороков, зависимость деформаций от напряжений близка к линейной, а прочность достигает 100 МПа.

Однако прочность реальной древесины при растяжении, учитывая ее значительные колебания, большое влияние пороков и длительности нагружения значительно ниже: для неклееной древесины I сорта R_р=10 МПа, для клееной древесины влияние пороков уменьшается, поэтому R_р=12 МПа. Прочность растянутых элементов в тех местах, где есть ослабления снижается в результате концентрации напряжений у их краев, т.е. вводится коэффициент условия работы m₀=0,8. Тогда получается расчетное сопротивление R_р=8 МПа. Проверочный расчет растянутых элементов производится по формуле:

σ , где

• 
  –площадь рассматриваемого поперечного сечения, причем ослабления, расположенные на участке длиной 20 см. считаются совмещенными в одном сечении. Для подбора сечений пользуются этой же формулой, но относительно искомой (требуемой) площади  .
  

9. 
   Работа элементов цельного сечения из дерева на сжатие с изгибом. Расчет элементов цельного сечения из древесины на сжатие с изгибом.