Структуры данных и эффективность алгоритмов. 4
 Скачать 2.32 Mb. Скачать 2.32 Mb.
|
Структуры данных и эффективность алгоритмов.Любой алгоритм (хороший или плохой) требует одной или более структур данных для представления элементов проблемы, которую нужно решить, и информации, вычисляемой в процессе решения. Структура данных - это набор данных, связанных специальным образом. Хотя понятие «структура данных» (прежде всего) означает определенный способ организации взаимосвязей между компонентами (и способ представления этих взаимосвязей), но по существу подразумевает и набор операций для работы с ее компонентами. Для одних и тех же данных различные структуры могут занимать неодинаковое пространство памяти. Одни и те же операции с различными структурами данных дают алгоритмы неодинаковой эффективности по времени и памяти. Простые алгоритмы могут порождать сложные структуры данных и наоборот, сложные алгоритмы могут использовать простые структуры данных. Программисты постоянно изыскивают способы повышения быстродействия или экономии пространства памяти за счет оптимального выбора организации данных и управления ими. При решении достаточно простых задач выбор того или иного подхода вряд ли имеет особое значение, если только выбранный подход приводит к правильному решению. Однако, при решении сложных задач (или в приложениях, в которых приходится решать очень большое количество простых задач) мы немедленно сталкиваемся с необходимостью разработки методов, при которых время или память используются с максимальной эффективностью. Пример 1. Построение ряда Фарея. Построить ряд Фарея Fn порядка n - последовательность всех несократимых дробей:
Например, для n=6: 0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1/1. Можно конечно сначала построить последовательность всех дробей со знаменателем, не превосходящим n, потом отсеять сократимые и упорядочить оставшиеся. Но остается неприятный осадок – а насколько обоснована необходимость такого, в общем-то, окольного пути с не ясно насколько нужными и обременительными промежуточными вычислениями. Можно попробовать строить последовательность сразу в требуемом порядке. Но быстро проясняется, что построение очередных элементов этого ряда связано с подбором нужного из возрастающего количества кандидатов. В теории чисел доказано, что ряд Фарея Fn можно строить, используя рекуррентное соотношение:
А это уже почти программа. При этом, поскольку речь идет о конечной последовательности, представляется естественным для хранения элементов ряда использовать структуру данных массив: VAR f:ARRAY[0..?] OF RECORD p,q:INTEGER END; BEGIN READ(n); //Строим F1: f[0].p:=0;f[0].q:=1;f[1].p:=1;f[1].q:=1;k:=2; //k число элементов ряда FOR i:=2 TO n DO BEGIN //Строим Fi по Fi-1, просматривая все пары соседних элементов: j:=0; WHILE j<=(k-2) DO BEGIN IF (f[j].q+f[j+1].q)=i THEN BEGIN //вставляем новый; j:=j+1;k:=k+1 END; j:=j+1 END END END. Из приведенной реализации хорошо видно, что использование обычного массива приводит к появлению операций сдвига сегментов этого массива, количество которых возрастает, т.к. «вставляем новый» предполагает следующие действия:
...причём один и тот же элемент придется перемещать (на одну позицию) многократно, а точнее ровно столько раз, сколько вставок до него понадобиться сделать (знать бы «сколько», можно было бы сразу положить «куда надо»!). Можно ли устранить «повторное вычисление»? Проанализируем ситуацию, попытаемся понять причину появления этого «повторного вычисления», возможно яснее станет, как устранить причину, а тогда возможно пропадут и последствия... Алгоритм в явном виде использует два отношения порядка:
Если хранить в порядке возрастания, то получаем проблему «сдвигов», а если хранить в порядке появления, то получаем проблему «как вычислить значение нового элемента» (проблему «подбора»). Выбранная структура представления данных задает единственный вариант перебора её элементов – в порядке индексации. Можно ли модифицировать структуру данных для хранения информации об обоих порядках? - подобрать способ хранения, подходящий и для добавления новых элементов, и для просмотра в порядке возрастания. Ответ положительный, такой способ хранения имеется:
Для n=6 – структура выглядит следующим образом: 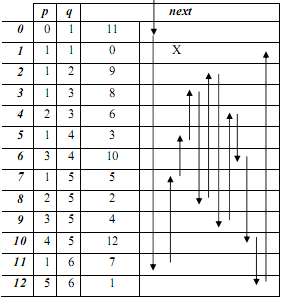 Рис. 1. Иллюстрация порядка следования элементов ряда С учетом выбранной структуры данных наша программа примет следующий вид: VAR f:ARRAY[0..?] OF RECORD p,q,next:INTEGER END; BEGIN READ(n); //Строим f[0].p:=0; f[0].q:=1; f[0].next:=1; f[1].p:=1; f[1].q:=1; f[1].next:=0; k:=2; FOR i:=2 TO n DO //Строим ряд //элементов в BEGIN j1:=0; j2:=f[j1].next; WHILE j2<>0 DO //второй в этой паре имеется BEGIN IF (f[j1].q+f[j2].q)=i THEN BEGIN //вставляем новый элемент ряда между ними: //добавить в конец: f[k].p:=f[j1].p+f[j2].p; f[k].q:=i; //связать по возрастанию: f[k].next:=j2; f[j1].next:=k; //учесть новый: k:=k+1 END; //перейти к следующей паре элементов: j1:=j2; j2:=f[j1].next END END END. Мы подобрали структуру данных, которая позволяет: хранить последовательность в порядке возрастания её элементов и эффективно выполнять для неё операцию «вставить» (элемент в текущую позицию) без обременительных расходов на «сдвиги». Это классическая структура данных – связанный список. Но вопросы ещё остались:
Чтобы конструктивно обсуждать эти вопросы и сравнивать различные подходы, нужна подходящая мера для используемых ресурсов - времени работы и объема памяти. Пример 2. Лексикографическая сортировка [2 п.3.2.]. Упорядочить последовательность (длины n) слов (длины k) в алфавите a..z. Обозначим через i[m..k] последовательность символов с номерами от m до k для слова i. Проведем рассуждение, используя классический метод последовательных уточнений:
В итоге снова получим последовательность , но уже упорядоченную в смысле: i≤j i[(m-1)..k]≤j[(m-1)..k] (т.е. теперь видим подальше до (m-1)-го символа). При этом необходимо соблюдать следующие условия распределения и сборки:
Таким образом, слова в после сборки будут упорядочены по символу в (m-1)-й позиции, а внутри пачки с одинаковым символом в этой позиции слова будут упорядочены как в до распределения. Любая исходная последовательность является упорядоченной в вышеописанном смысле при m=k+1 (т.е. в начальной ситуации, когда мы совсем плохо видим...), а на каждом шаге мы получаем более точную упорядоченность, неумолимо приближаясь к решению задачи при m=1. Какие структуры данных потребуются для реализации этого алгоритма:
Использование в такого массива строк представляется изначально избыточным. Просчитать заранее, сколько строк должен содержать один карман не удается, это определяется исходной последовательностью. В самом деле, каждый карман может оказаться пустым в результате текущего распределения, а с другой стороны – все слова из последовательности могут попасть в один из карманов. Однако предложенный вариант опять оставляет неприятный осадок – для хранения n слов приходится резервировать пространство памяти, способное хранить 26*n слов. Устранить этот необоснованный перерасход памяти можно с помощью структуры данных «связанный список». // Здесь будем хранить последовательность : : ARRAY[1..n] OF RECORD w:STRING[k]; next:0..n END; // В случае связного представления последовательности // нет необходимости перемещать её элементы, достаточно // изменять только связи между ними. Поэтому в будем // хранить не элементы, а только номера позиций первого и // последнего элемента каждого кармана. Сами элементы будут // оставаться в на своих местах, но связи между ними надо // будет аккуратно корректировать в соответствии с порядком, // определяемым внутри каждого из карманов: : ARRAY[‘a’..’z’] OF RECORD first,last:0..n END; // Сохраним входную последовательность в связанном списке // : FOR i:=1 TO n-1 DO BEGIN READLN([i].w);[i].next:=i+1 END; READLN([n].w); [n].next:=0; first:=1; last:=n; // Выполним k распределений-сборок: FOR m:=k DOWNTO 1 DO BEGIN // Очистим карманы: FOR s:=’a’ TO ’z’ DO BEGIN [s].first:=0;[s].last:=0 END; // Распределим слова последовательности по карманам: i:=first; WHILE i<>0 DO BEGIN s:=[i].w[m]; IF [s].first=0 THEN {карман был пустой:} BEGIN [s].first:=i; [s].last:=i END ELSE BEGIN j:=[s].last; [j].next:=i END; [s].last:=i; i:=[i].next; [[s].last].next:=0 END; // Теперь вместо одной последовательности, начинающейся // в позиции с номером first, имеем несколько // последовательностей, начинающихся в позициях // [s].first (для s: a..z) // Проведем сборку , причем учтем, что нет необходимости // корректировать все связи, достаточно только связать // последний элемент каждого кармана с первым элементом // следующего кармана: first:=0; last:=0; FOR s:=‘a’ TO ’z’ DO BEGIN j:=[s].first; IF j<>0 THEN BEGIN {карман не пустой:} IF first=0 THEN first:=j ELSE [last].next:=j; last:=[s].last END END END Мы подобрали структуру данных, которая позволяет устранить вышеотмеченный необоснованный перерасход памяти, правда дополнительное пространство памяти для организации связного спискового представления последовательностей всё же потребуется. |
