Структуры данных и эффективность алгоритмов. 4
 Скачать 2.32 Mb.
|
Построение модели задачи. Процедурная абстракция и абстракция данных.Хороший подход к разработке эффективного алгоритма для данной задачи - изучить ее сущность. Часто задачу можно сформулировать на языке основных математических понятий, таких, как множество, и тогда алгоритм для нее можно изложить в терминах основных операций над основными объектами. Преимущество такой точки зрения в том, что можно проанализировать несколько различных структур данных и выбрать из них ту, которая лучше всего подходит для задачи в целом. Таким образом, разработка хорошей структуры данных идет рука об руку с разработкой хорошего алгоритма. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. [2] В любой задаче имеются определенные информационные связи между данными и структура данных должна в определенной степени эти связи отображать. Если в структуре данных это соответствие представлено не адекватно (недостаточно полно), то соответствующее приведение придется делать на уровне алгоритма, что увеличит время его работы. Снова вернемся к задаче о ряде Фарея, а точнее к алгоритму ее решения, основанному на рекуррентном соотношении построения этого ряда. Видимо мы слишком поторопились с выбором конкретной структуры данных, слишком банально сделан вывод – раз уж речь идет о конечной последовательности, значит необходимо использовать векторы ARRAY[0..?] OF RECORD p,q:INTEGER END. Но информационные связи между элементами этой последовательности более сложны, чем между элементами просто вектора, с одной стороны они связаны в последовательность по определению - в порядке возрастания, а с другой стороны рекуррентное соотношение связывает их порядком порождения. Алгебраический взгляд на модель задачи позволяет зафиксировать операциональную составляющую (а может быть и сущность) имеющихся информационных связей между данными. И все-таки в этом алгоритме речь идет о (конечной) последовательности и об операциях с нею:
Такова модель этой задачи, в терминах которой рекуррентным соотношением собственно и описан алгоритм ее решения. Если мы знакомы с проблематикой структур данных, то видимо, знаем – в случае представления последовательности массивом операция вставки реализуется плохо, а хорошо она реализуется именно в случае представления связанным списком, причем для данного случая достаточен односторонний список (с понятием «текущая позиция»), так как необходим только последовательный просмотр. Аналогичная ситуация и со второй задачей - о лексикографической сортировке. Можно по-разному формулировать причину перерасхода памяти в первой версии представления данных:
Но при более детальном анализе ситуации становится ясно, что это скорее следствие другой, более глубокой причины.
Но если попытаться решать эту задачу «разбить-собрать», например, перестановками элементов внутри массива, то мы сразу столкнемся с проблемой «тесноты»: надо положить элемент в сегмент массива, запланированный для соответствующего кармана, но там лежит другой (еще не квалифицированный элемент), сначала его куда-то надо перемещать. Фактически, причину возникающей проблемы можно сформулировать ровно так же, как и в предыдущей задаче – у текущей последовательности свой порядок, у каждой подпоследовательности (в кармане) свой, а собираемая последовательность будет иметь свой - как и где хранить информацию обо всех этих порядках, ведь ими надо пользоваться в процессе обработки. И все-таки причины (видимо всегда) лежат в информационных связях между данными задачи, а вскрывать и описывать их можно по-разному... С алгебраической точки зрения, модель этой задачи, в терминах которой собственно и было проведено рассуждение методом последовательных уточнений - мы работаем с набором последовательностей, с которыми выполняются операции: последовательного просмотра, исключения и включения элементов, а также операции сцепления последовательностей. Но приведенная формулировка операций излишне грубовата и приведет к выбору структуры данных с излишними возможностями и излишними расходами на их реализацию. Аккуратный анализ рассуждения, обоснования алгоритма лексикографической сортировки, дает более детальную формулировку операций:
Связное представление последовательностей позволяет реализовать такой набор операций эффективно как по времени, так и по памяти, причем с учетом особенностей алгоритма решения задачи ясно, что объем используемой памяти будет оставаться фиксированным и (почти) равным объему исходной последовательности. Лексикографическим порядком на множестве векторов различной длины, построенных над конечным алфавитом  называется такая последовательность, для которой выполнение условия  ,   , означает, что выполнено одно из условий: 1) существует такое целое число  , что  и для всех  справедливо  2)  и при  .Например, обычно основы слов в словарях расположены в лексикографическом порядке. Задача: Используя идею лексикографической сортировки для слов одинаковой длины, написать алгоритм лексикографической сортировки цепочек в общем случае Пример 3. Связность [3 гл.1.].3 Предположим, что имеется последовательность пар целых чисел, в которой каждое целое число представляет объект некоторого типа, а пара p-q интерпретируется в значении «р связано с q». Мы предполагаем, что отношение «связано с» является симметричным 4 и транзитивным 5 (т.е. это отношение эквивалентности). Задача состоит в написании программы исключения лишних пар:
Пример решения задачи показан на рис.2. Таким образом, задача состоит в разработке программы, которая может запомнить достаточный объем информации о просмотренных парах, чтобы решить, связана ли новая пара объектов. Рис 2. ПРИМЕР СВЯЗНОСТИ Для заданной последовательности пар целых чисел, представляющих связь между объектами (слева), задача алгоритма связности заключается в выводе тех пар, которые обеспечивают новые связи (в центре). Например, пара 2-9 не должна выводиться, поскольку связь 2-3-4-9 определяется ранее полученными связями (подтверждение этого показано справа). Подобная задача возникает в ряде важных приложений. Например, числа р и q могли бы представлять номера компьютеров в большой сети, а пары могли бы представлять соединения в сети. Тогда такая программа могла бы использоваться для определения того, нужно ли устанавливать новое прямое соединение между р и q, чтобы иметь возможность обмениваться информацией, или же можно было бы использовать существующие соединения для установки коммуникационного пути. Отметим, уже в формулировке задачи мы абстрагировались от конкретного содержания объектов (и способа их представления), ограничившись тем, что нам известны идентифицирующие их ключи (р,q...). От конкретного содержания связей между объектами мы тоже абстрагировались, например, от пропускной способности соединений в той самой сети компьютеров. Возможно, это не помешает применению нашего алгоритма в соответствующем приложении, а возможно потребуется его соответствующая адаптация к более детальным условиям приложения. Рассмотрим модель для нашей задачи. При получении каждой новой пары вначале необходимо определить, представляет ли она новое соединение, и если представляет, то внедрить информацию об обнаруженном соединении в общую картину о связности объектов для проверки соединений, которые будут наблюдаться в будущем. Эту текущую «общую картину о связности» можно описать семейством множеств, каждое множество включает все связанные (между собой) объекты (возможно через промежуточные связи) и никакая пара множеств в семействе не пересекается (т.е. множество – это класс эквивалентности, а семейство – разбиение универсума всех элементов на классы эквивалентности). Таким образом, модель нашей задачи задается:
Решение задачи связности в терминах этой модели описывается так:
Теперь рассмотрим несколько вариантов выбора структур данных для представления таких семейств множеств, а для них соответствующие варианты реализации интересующих нас операций и варианты программ решения нашей задачи о связности. Для устранения деталей, отвлекающих от основных целей, будем считать, что на вход могут поступать только целые числа из полуинтервала [0,N). Программа 3.1. Решение задачи связности методом быстрого поиска.
Вспомним классическое представление множеств с помощью характеристических 0-1-векторов и воспользуемся подходящим его обобщением: id: ARRAY[0..N-1] OF INTEGER; Каждому числу p из [0,N) соответствует в этом массиве p-я позиция, а значение id[p] – представляет имя множества, которому p принадлежит (т.е. p id[p]). Множества мы будем идентифицировать одним из чисел, ему принадлежащих (т.е. представителем класса эквивалентности, в соответствии с общематематической терминологией).
find(p)=id[p] – операция «найти» реализуется очень хорошо, именно поэтому этот вариант и назван методом «быстрого поиска». Но операцию union(t,s) эффективно реализовать не удается, придется просмотреть весь id. Будем интерпретировать union(t,s) как t:=ts, требуемый результат мы получим, если во всех позициях id, в которых id[i]=s (что означает is), проставим t(что означает - теперь it). // Обозначим именем i одноэлементное множество {i} и // инициализируем id семейством всех одноэлементных множеств: FOR i:=0 TO N-1 DO id[i]:=i; // Приступаем к обработке входной последовательности: WHILE NOT EOF(input) DO BEGIN READLN(p,q); t:=id[p]; // t:=find(p) IF t<>id[q] THEN{p,q – пока не связаны} BEGIN WRITELN(p,q); // А теперь пополним текущую «общую картину о связности»: // union(id[q],id[p]): id[q]:=id[q]id[p] : FOR i:=0 TO N-1 DO IF t=id[i] THEN id[i]:=id[q] END END Причина больших затрат времени на выполнение операции «объединить» была заложена изначально в структуре данных, выбранной для представления семейства множеств, она запредельно ориентирована на быстрый поиск, явно в ущерб для операции «объединить». Массив, как известно, это (таблично заданная хранимая) функция. Прямой доступ к элементам этой структуры данных обеспечивает «быстрый поиск». С другой стороны, в способе представления этой функции заложена необходимость тиражировать имя множества для каждого элемента этого множества. Отсюда и проистекает необходимость массовых корректировок, когда имя множества меняется. В структуре данных этого алгоритма множество p определяется как p={i[0..N)/id[i]=p}, т.е. можно сказать и так – каждый элемент (i) множества указывает на элемент (p), представляющий это множество. Если иметь в виду такую трактовку, то полезно посмотреть рис 3, где приведено графическое представление состояний массива id в процессе выполнения программы 3.1. 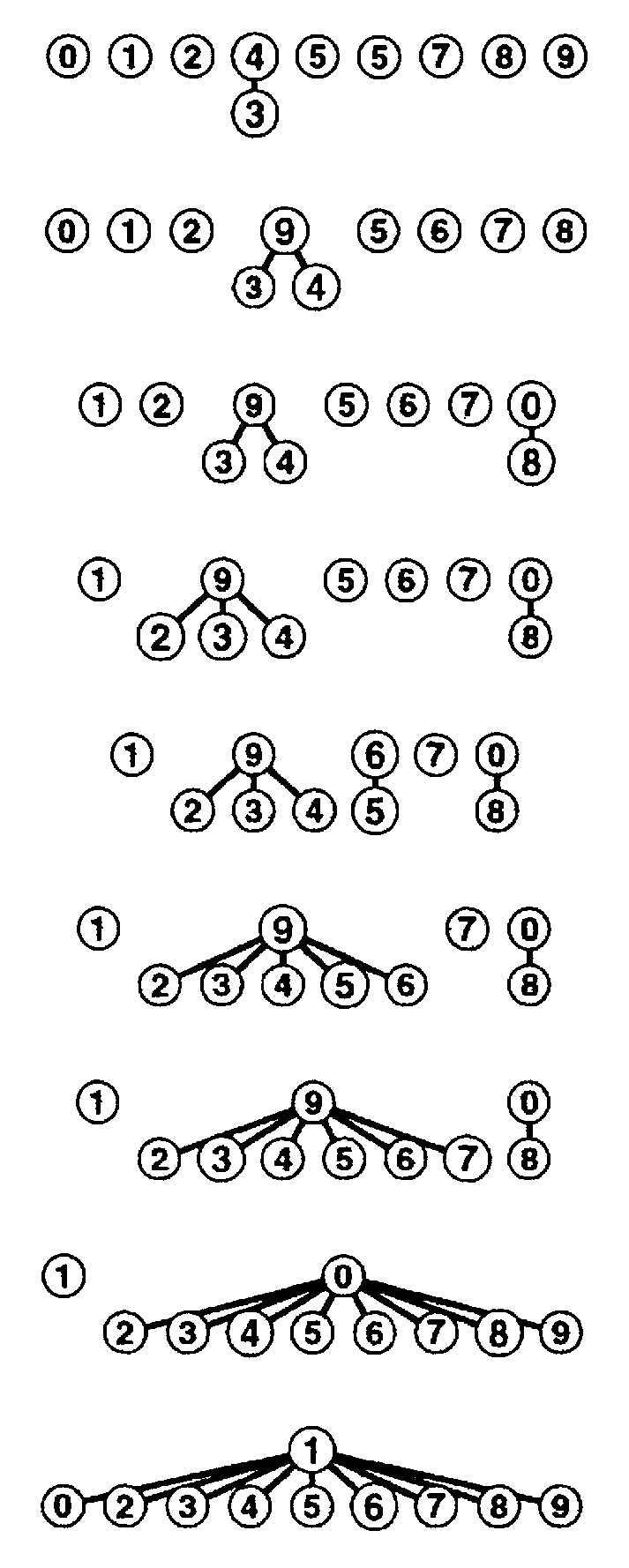 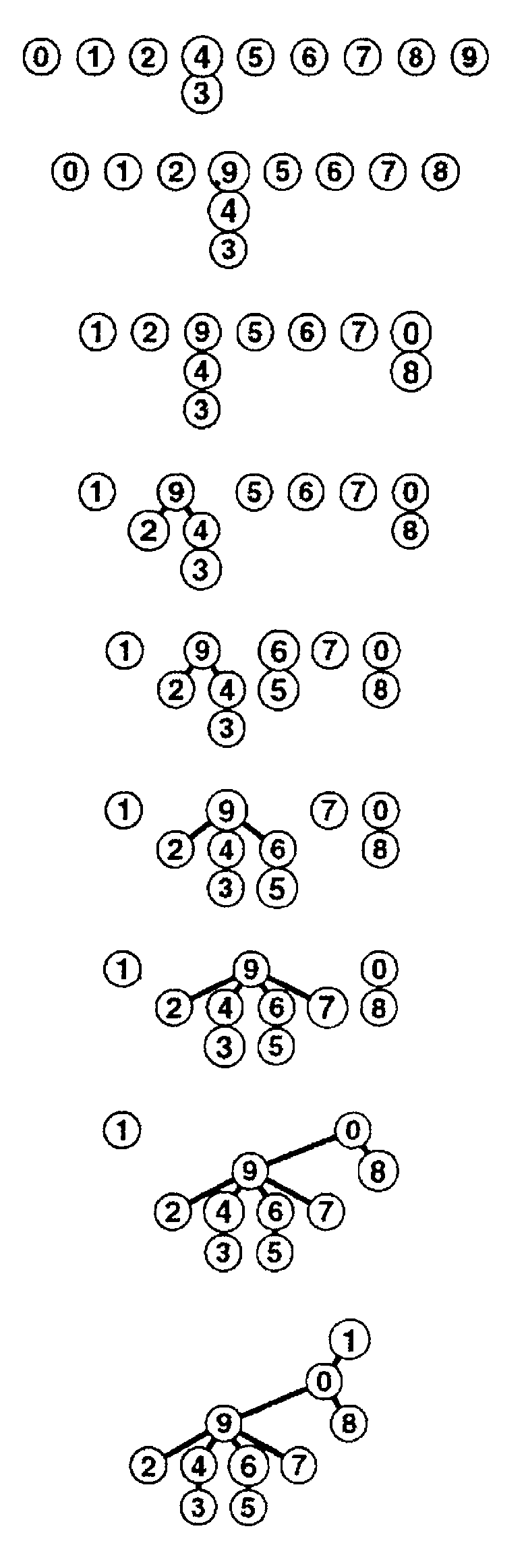 Рис 3. Представление быстрого поиска в виде дерева для примера, приведенного на рис 2. Рис 4. Представление быстрого объединения в виде дерева для примера, приведенного на рис 2. Рисунок наглядно иллюстрирует: почему время поиска хорошее – потому что путь от элемента к множеству предельно короткий (одно ребро), а почему время объединения плохое – потому что всем элементам одного из множеств надо изменить указатель на представителя множества – результата объединения (это не считая того, что эти элементы надо еще найти). Программа 3.2. Решение задачи связности методом быстрого объединения. Этот алгоритм основан на методе двойственном предыдущему, теперь акцентируем основное внимание именно на быстром объединении. В основе этого алгоритма лежит та же структура данных – массив, индексированный по именам объектов. Но в нем используется иная интерпретация значений, что приводит к более сложной структуре данных. Иная интерпретация значений массива id означает иное представление той функции id, о которой говорилось выше. Ясно, что если бы имя множества, которому принадлежит элемент, не тиражировалось, то и не было бы проблемы массовой корректировки при выполнении операции объединения. Вспомним решение задачи о лексикографической сортировке, в котором операция «сцепить» две последовательности выполнялась одним действием – связать последний элемент первой последовательности с первым элементом второй. Это хорошо известная типовая возможность связного представления данных, причем она применима при определенных условиях не только к связным спискам, а к любым связным структурам.
id: ARRAY[0..N-1] OF INTEGER; Как и раньше, множества мы будем идентифицировать представителем - одним из чисел, которые ему принадлежат. Но теперь будем допускать, что элемент множества не обязательно сразу указывает на элемент, представляющий это множество, а возможно указывает на другой элемент, тоже принадлежащий этому множеству и т.д. вплоть до элемента, указывающего на себя, т.е. id[p]=p. Такой элемент p и используется в качестве представителя множества p. Точнее, если: i0, id[i0]=i1, id[i1]=i2,... id[ik]=p, id[p]=p то i0,i1,i2,... ik,p p (как множеству с именем p), причем в таких цепочках по указателям естественно запрещены циклы (но есть петля в конце). Отметим, что приведенное определение не означает, что множества представляются обязательно цепочками. В общем случае множество представляется деревом, а в этом определении речь идет только об одной из ветвей такого дерева (от вершины i0 до корня p). Т.е. множество p определяется как p={i[0..N)/id[id[...id[i]...]]=p=id[p]}(  ).Теперь функция id (для элемента возвращающая имя множества, которому принадлежит этот элемент) будет иметь в какой-то части табличное представление, а в какой-то вычислимое. Отсюда прогнозируются частично выгоды (прямого доступа к данным), а частично и затраты (на вычисления).
Операция union(t,s), в трактовке t:=ts, теперь реализуется очень просто. Поскольку t,s – корни представляющих деревьев, t=id[t] и s=id[s], то оператор id[s]:=t заставит каждый путь от элемента множества s до корня s этого дерева продолжить (одним переходом) до t – корня дерева t. Хуже дела обстоят с операцией find, согласно вышеприведенному определению:find(i)= id[id[...id[i]...]]=p=id[p], т.е. придется пройти путь от элемента до корня. // Обозначим именем i одноэлементное множество {i} и // инициализируем id семейством всех одноэлементных множеств: FOR i:=0 TO N-1 DO id[i]:=i; // Приступаем к обработке входной последовательности: WHILE NOT EOF(input) DO BEGIN READLN(p,q); t:=p; WHILE t<>id[t] DO t:=id[t]; // t:=find(p) j:=q; WHILE j<>id[j] DO j:=id[j]; // j:=find(q) IF t<>j THEN {p,q – пока не связаны} BEGIN WRITELN(p,q); // А теперь пополним текущую «общую картину о связности»: id[t]:=j // union(j,t): j:=jt END END Полезно посмотреть рис 4, где приведено графическое представление состояний массива id в процессе выполнения программы 3.2, и сравнить с рис 3 для программы 3.1. Рис 3.2 наглядно иллюстрирует характерные особенности программы 3.2 в использовании ресурса времени. Почему время поиска не очень хорошее – потому что путь от элемента к множеству теперь может оказаться многошаговым (несколько ребер). А почему время объединения очень хорошее – потому что объединение теперь не требует массовых изменений данных, только одна корректировка указателя на представителя множества – результата объединения. Интересно разобраться в двух вопросах: сравнить в целом эти два алгоритма в смысле эффективности по времени, и насколько в новом алгоритме могут быть велики затраты времени на выполнение операции «найти». Общие соображения и анализ графического представления типа рис. 3 - 4 для различных вариантов входной последовательности наводят на мысль, что новый алгоритм лучше, а экспериментальное тестирование этих программ может даже подтверждать такое заключение. Но внимательный анализ позволяет показать, что гарантий для такого заключения нет. Например, если пары вводятся в следующем порядке: 1-2, 1-3, 1-4 и т.д., то все элементы будут попадать в одно множество связности, а операция «объединить» будет связывать эти элементы в дерево с одной ветвью (1234...), длина которой постоянно возрастает. А значит, для каждой входной пары 1-p будет выполняться find(1), проходящий эту ветвь от листа 1 до (все более далекого) корня. Можно подсчитать, что на этой входной последовательности длины t алгоритм будет выполнять примерно t2 переходов по ребрам пути к корню дерева, а это реалистичная оценка времени работы алгоритма. Можно конечно сказать, что эта ситуация выправляется просто, надо запоминать, какому множеству принадлежит элемент 1. Но плохих, в аналогичном смысле, входных последовательностей можно построить сколько угодно, а сцепляя их в различных порядках можно полностью запутать картину – и придется это запоминать для каждого элемента, т.е. получается, что к новому представлению данных добавим предыдущее с вышерассмотренными проблемами его поддержания. Нетрудно показать, что на этом и аналогично плохих входах, новый алгоритм работает не лучше, чем предыдущий – он затрачивает много времени на операции «найти», а предыдущий затратит такое же время на операции «объединить» (фактически по той же самой причине). Аккуратными расчетами можно показать, что новый алгоритм не лучше предыдущего по времени в худшем, но все же лучше – по времени в среднем (что обычно и проявляется в экспериментальном тестировании). Обнаруженная причина возможно очень плохого времени выполнения операции «найти» заключена в возможности получить очень разбалансированное дерево. Если бы удалось гарантировать, что дерево постоянно ветвится, причем на поддеревья примерно одинакового объема (например, по количеству вершин), то очень длинных ветвей не могло бы быть из мощностных соображений (в ветвящемся дереве с очень длинными ветвями очень много элементов). Эту идею мы и попытаемся реализовать в следующем алгоритме. Программа 3.3. Решение задачи связности методом взвешенного быстрого объединения. Предыдущий алгоритм можно легко модифицировать, чтобы худшие случаи, подобные вышерассмотренному, гарантированно не могли появиться. Вместо того чтобы произвольным образом соединять второе дерево с первым при выполнении операции union, будем отслеживать количество вершин в каждом дереве и всегда присоединять меньшее дерево к большему, это позволит поддерживать приемлемую сбалансированность деревьев. Это изменение требует наличия еще одного массива для хранения количества вершин в деревьях, но оно ведет к существенному повышению эффективности, причем гарантированному, т.е. по времени в худшем. Как было сказано выше, нам потребуется дополнительный массив sz: ARRAY[0..N-1] OF INTEGER; Для каждого i, у которого id[i]=i, т.е. i является корнем дерева (представителем класса эквивалентности), в sz[i] будем хранить количество вершин в дереве с корнем i (т.е. мощность множества – класса эквивалентности i). // Инициализируем id семейством всех одноэлементных множеств, // а sz – соответственно объемами этих множеств. FOR i:=0 TO N-1 DO BEGIN id[i]:=i; sz[i]:=1 END; // Приступаем к обработке входной последовательности: WHILE NOT EOF(input) DO BEGIN READLN(p,q); t:=p; WHILE t<>id[t] DO t:=id[t]; // t:=find(p) j:=q; WHILE j<>id[j] DO j:=id[j]; // j:=find(q) IF t<>j THEN {p,q – пока не связаны} BEGIN WRITELN(p,q); // А теперь пополним текущую «общую картину о связности»: IF sz[t] // union(j,t): j:=jt: к большему j подсоединяем меньшее t BEGIN id[t]:=j; sz[j]:=sz[j]+sz[t] END ELSE // множество j меньше множества t // union(t,j): t:=tj: к большему t подсоединяем меньшее j BEGIN id[j]:=t; sz[t]:=sz[t]+sz[j] END END END Рис. 5 в сравнении с рис. 4 наглядно иллюстрирует характерные особенности деревьев, которые строит программа 3.3, для представления соответствующих множеств. Они явно лучше сбалансированы и длины путей, как правило, заметно меньше. А значит на выполнение операций «найти» будет заметно меньше расходоваться времени. И все же, что меньше и почему меньше, более или менее ясно, а насколько меньше? 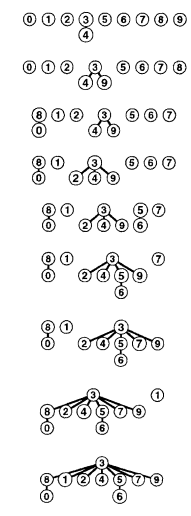 Рис. 5 Представление взвешенного быстрого объединения в виде дерева Характеризующая особенность деревьев, которые будет строить этот алгоритм, состоит в следующем:
На этой последовательности рисунков демонстрируется результат изменения алгоритма быстрого объединения для связывания корня меньшего из двух деревьев с корнем большего из деревьев. Расстояние от каждого узла до корня его дерева не велико, поэтому операция поиска выполняется эффективно. Аккуратными расчетами можно показать, что у сбалансированных деревьев длина пути не может превосходить логарифма (двоичного) от количества вершин. Лемма Для определения того, связаны ли два из N объектов, алгоритму взвешенного быстрого объединения требуется отследить максимум lg N указателей. При объединении набора, состоящего из i узлов, с набором, состоящим из j узлов, при  количество указателей, которые должны отслеживаться в меньшем наборе, увеличивается на 1, но теперь узлы находятся в наборе размера i+j, и, следовательно, свойство остается справедливым, поскольку 1 + lg i = lg(2i) = lg(i + i) < lg(i + j). А это уже гарантия совсем неплохого времени выполнения операции «найти» при очень хорошем времени выполнения операции «объединить». Кстати, идею взвешенного объединения (вливания меньшего множества в большее) можно применить и для алгоритма быстрого поиска. Тогда существенно сократится количество необходимых корректировок при вливании множества, содержащего id[i], в другое множество. Но это не улучшит алгоритм, потому что эти элементы id[i] надо еще найти. Но если иметь и поддерживать связный линейный список элементов для каждого множества (как в задаче о лексикографической сортировке), то алгоритм можно «дожать»... Получим двойственный алгоритм с аналогичными общими характеристиками, но с быстрым поиском и логарифмическим объединением 8. Итого, мы получили алгоритм, который на последовательности из M пар связности на N элементах, затрачивает примерно M*log2(N) времени в худшем случае. Это существенно лучше, чем предыдущие алгоритмы, для которых оценка по времени в худшем примерно M*N. Можно ли существенно улучить этот алгоритм? Оказывается можно. Программа 3.4. Решение задачи связности методом взвешенного быстрого объединения со сжатием пути. В предыдущем алгоритме нам удалось так организовать вычисления, что высота деревьев, представляющих множества, ограничена логарифмом от N. Если бы удалось ограничить высоту этих деревьев константой, то получили бы константное время для операции «поиск». Но это выглядит совсем не реалистично... однако встроить в программу преобразование, существенно уменьшающее высоту деревьев всегда можно. Вопрос только в том, окупятся ли затраты на это преобразование. Рассмотрим совсем простое преобразование. При выполнении операции «найти» приходится проходить путь от вершины, которую ищем, до корня дерева: t:=p; WHILE t<>id[t] DO t:=id[t]; Проходя этот путь, проведем реструктуризацию дерева: t:=p; WHILE t<>id[t] DO BEGIN id[t]:= id[id[t]]; t:=id[t] END; Суть приема не в том, что мы теперь в теле цикла выполняем два перехода за раз, а в том, что проходя путь: (i0i1i2i3i4i5i6i7i8i9...) мы разбиваем его на несколько путей более коротких: (i0i2i4i6i8...) (i1i2i4i6i8...) (i3i4i6i8...) ... Затраты на эту реструктуризацию не значимые, а если в будущем нам придется выполнять операцию «найти» для этих элементов, то она будет выполняться в два раза быстрее. // Инициализируем id семейством всех одноэлементных множеств, // а sz – соответственно объемами этих множеств. FOR i:=0 TO N-1 DO BEGIN id[i]:=i; sz[i]:=1 END; // Приступаем к обработке входной последовательности: WHILE NOT EOF(input) DO BEGIN READLN(p,q); t:=p;WHILE t<>id[t] DO BEGIN id[t]:=id[id[t]];t:=id[t] END; j:=q;WHILE j<>id[j] DO BEGIN id[j]:=id[id[j]];j:=id[j] END; IF t<>j THEN {p,q – пока не связаны} BEGIN WRITELN(p,q); // А теперь пополним текущую «общую картину о связности»: IF sz[t] // union(j,t): j:=jt: к большему j подсоединяем меньшее t BEGIN id[t]:=j; sz[j]:=sz[j]+sz[t] END ELSE // множество j меньше множества t // union(t,j): t:=tj: к большему t подсоединяем меньшее j BEGIN id[j]:=t; sz[t]:=sz[t]+sz[j] END END END 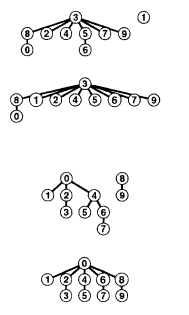 Рис. 6. Сжатие пути В общем виде, алгоритмы сжатия для эффективного поиска осуществляют следующее преобразование 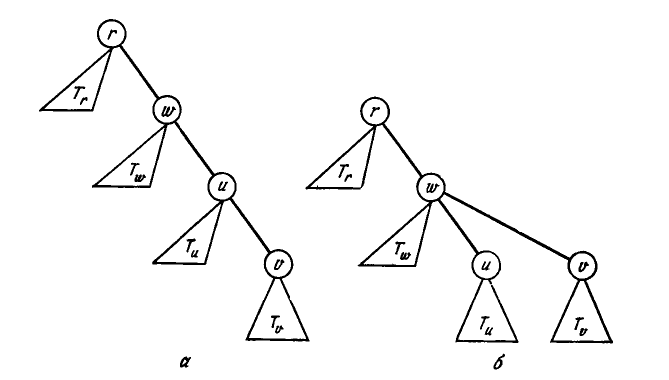 Рис. 7. Реализация поиска со сжатием пути Экспериментальное тестирование этой программы на длинных входных последовательностях покажет почти линейную зависимость времени работы от длины входа[3]. 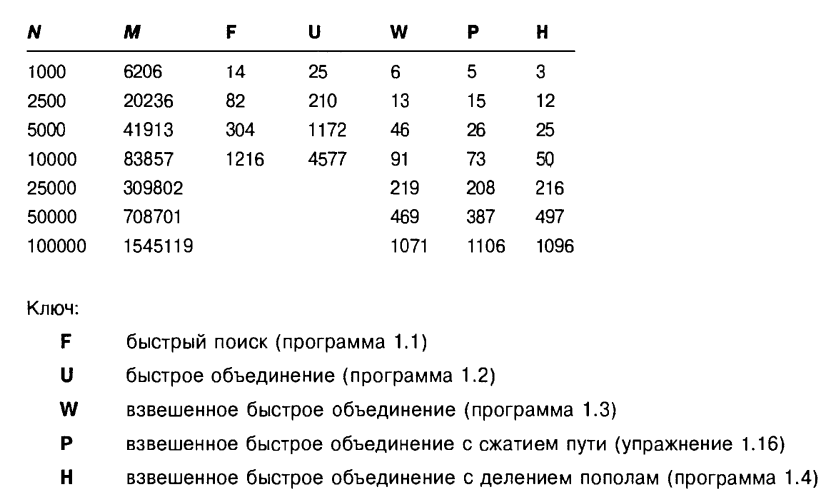 И это не случайно. Для варианта полного сжатия, когда при реструктуризации дерева все вершины пути, проходимого операцией «найти», привязываются к корню, доказана почти линейная оценка времени в худшем:
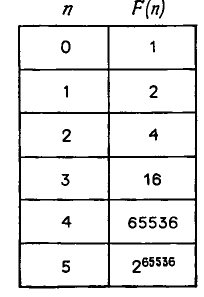 Рис. 8 Несколько значений функции F
Верхняя оценка времени работы такого алгоритма в худшем на (достаточно длинных) входах длины M равна C*M*G(N) для подходящей константы C 9. Подведем некоторые итоги. В этом разделе мы руководствовались следующей стратегией в изложении материала о разработке алгоритмов решения задач:
Потенциальная возможность впечатляющего повышения производительности алгоритмов решения реальных задач делает разработку алгоритмов увлекательной областью исследования; лишь немногие другие области разработки позволяют обеспечить экономию времени в миллионы, миллиарды и более раз. Что еще важнее, по мере повышения вычислительных возможностей компьютеров разрыв между быстрыми и медленными алгоритмами увеличивается. Новый компьютер может работать в 10 раз быстрее и может обрабатывать в 10 раз больше данных, чем старый, но при использовании квадратичного алгоритма новому компьютеру потребуется в 10 раз больше времени для выполнения новой задачи, чем требовалось старому для выполнению старой! Вначале это утверждение кажется противоречивым, но его легко подтвердить простым тождеством  . По мере того как вычислительные мощности увеличиваются, позволяя решать все более сложные задачи, важность использования эффективных алгоритмов также возрастает.Разработка эффективного алгоритма приносит моральное удовлетворение и прямо окупается на практике. Как видно на примере решения задачи связности, просто сформулированная задача может приводить к изучению множества алгоритмов, которые не только полезны и интересны, но и представляют увлекательную и сложную для понимания задачу. Осознанное абстрагирование от способа представления объектов задачи (абстракция данных) и способа реализации операций с этими объектами (процедурная абстракция) приводит нас к понятию абстрактный тип данных, к соответствующей технологии разработки алгоритмов решения задач и их программной реализации. Основные понятия. |
при 