|
|
Структуры данных и эффективность алгоритмов. 4
Пример 4. Рассмотрим вычисление полинома 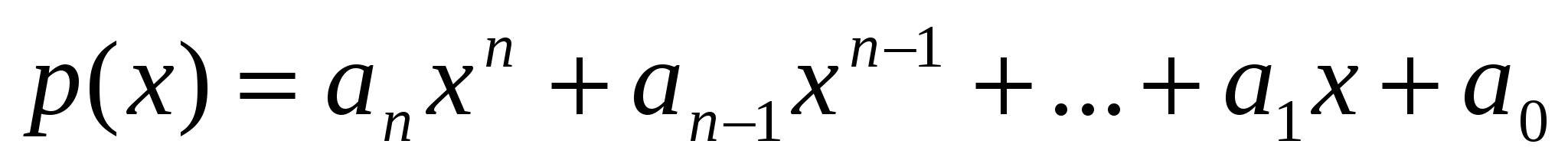 Входными переменными служат коэффициенты и неопределенная переменная х Выходной переменной будет значение полинома р.
По правилу Горнера для вычисления 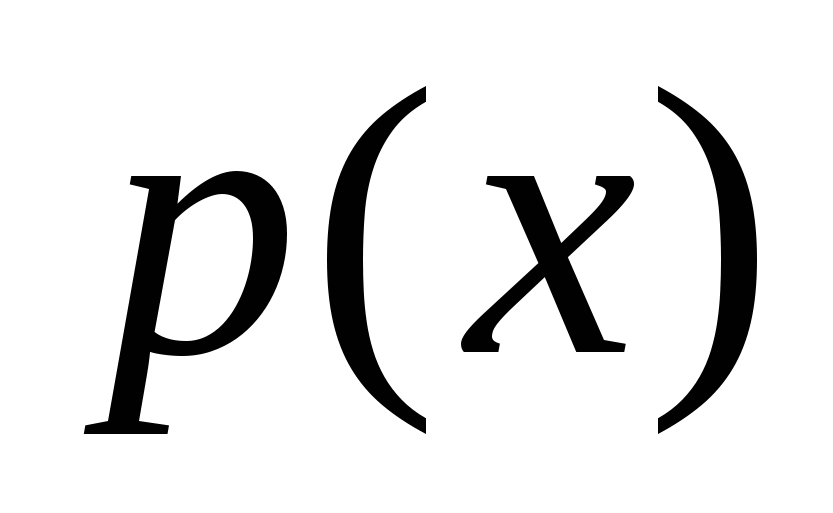 можно использовать алгоритм: можно использовать алгоритм:
1) 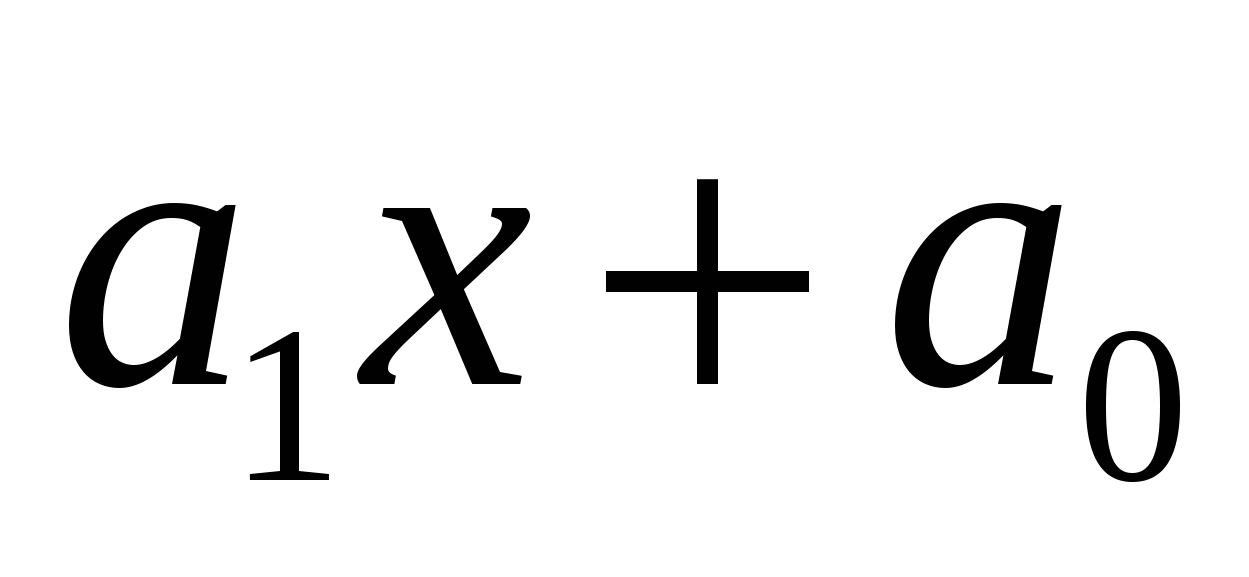 для n=1, для n=1, 2) 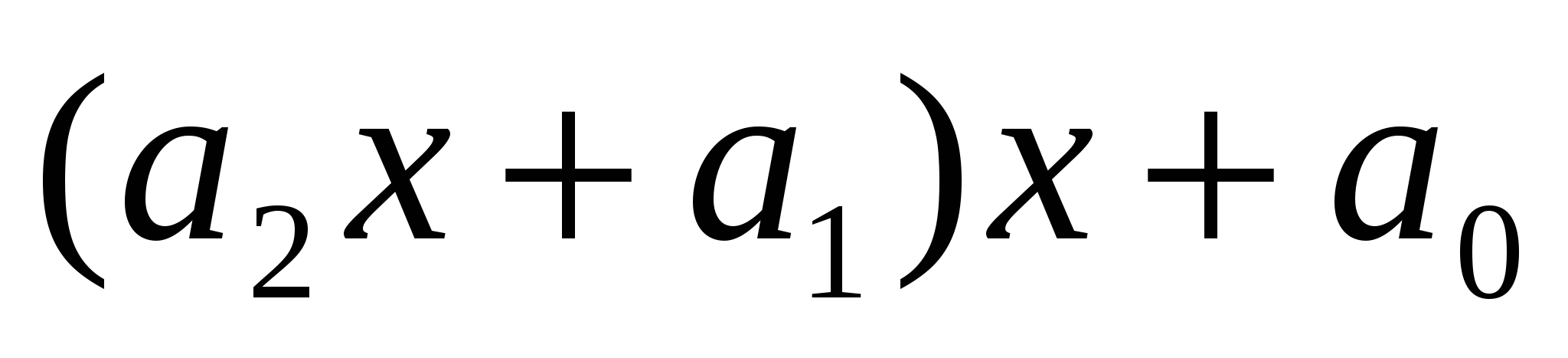 для п=2, для п=2,
3) 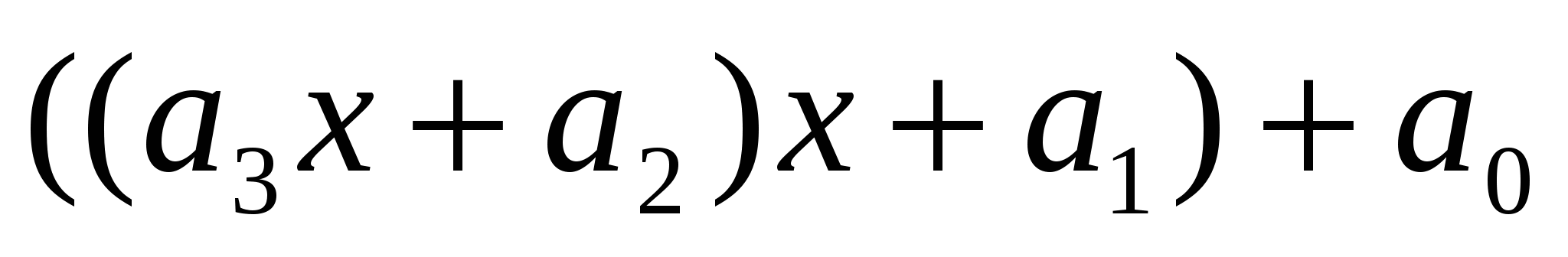 для для 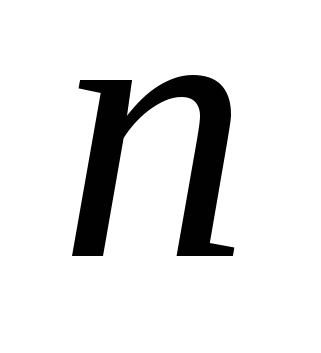 =3 =3
Если брать в качестве модели вычислений неветвящуюся программу, то временная сложность последовательности программ равна числу шагов 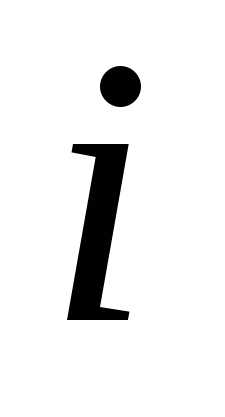 -й программы как фукции от -й программы как фукции от 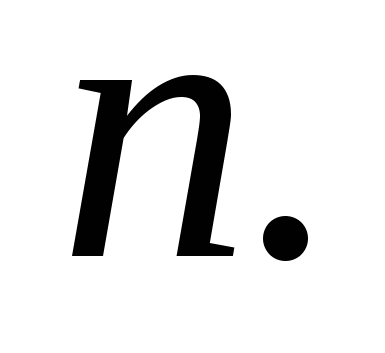 Заметим, что измерение временной сложности есть не что иное, как подсчет числа арифметических операций. Заметим, что измерение временной сложности есть не что иное, как подсчет числа арифметических операций.
2. Битовые вычисления (схемы из функциональных элементов)
Существует простая модификация модели неветвящихся программ, которая соответствует логарифмической весовой функции. Эта модель, называемая битовым вычислением, по существу, является той же неветвящейся программой, но только в ней 1) все переменные принимают значения 0 или 1, т. е. это биты, 2) используются логические операции вместо арифметических (and обозначается через &, or — через  . exclusive or — через . exclusive or — через  , not — через — , not — через — ). ).
3. Операции с двоичными векторами
Можно было бы не ограничивать значения переменных символами 0 и 1, а разрешить переменным принимать в качестве значения любой вектор из 0 и 1. Фактически двоичные векторы фиксированной длины очевидным образом соответствуют целым числам, так что здесь не допускается ничего такого, что не допускалось бы в РАМ, т. е., когда это удобно, просто разрешаются регистры неограниченного размера.
Деревья решений
Выше приведены три модификации РАМ, игнорирующие команды разветвления и учитывающие только те шаги программы, которые включают арифметический счет. В некоторых задачах удобно в качестве основной меры сложности брать число выполняемых команд разветвления. В случае сортировки, например, выходы совпадают со входами с точностью до порядка. Поэтому разумно рассматривать модель, в которой все шаги дают разветвления, возникающие в результате сравнения двух величин. Обычно программу, состоящую из разветвлений, представляют в виде двоичного дерева, называемого деревом решений. Каждый внутренний узел представляет один из шагов решения. Сравнение, представленное корнем, выполняется первым, и затем "управление" передается одному из его сыновей в зависимости от исхода теста до тех пор, пока не будет достигнут лист дерева. Нужный результат находится на достигнутом листе
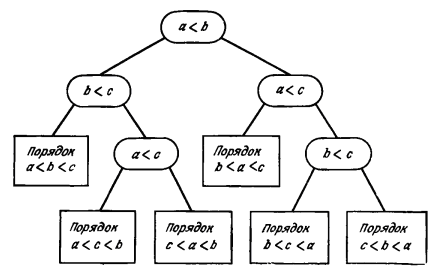
Рис. 10. Дерево решений для задачи сортировки трех чисел 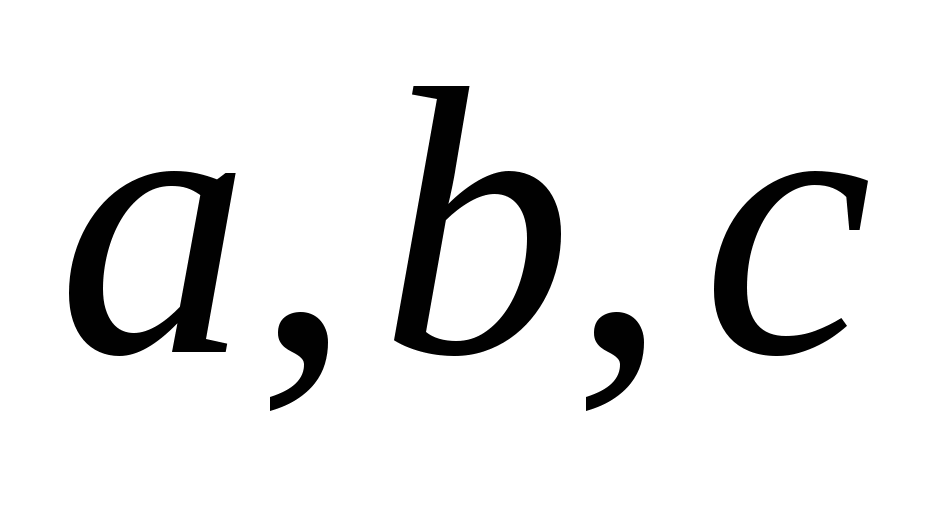
Асимптотические обозначения.
Время выполнения программы описывается некоторой функцией 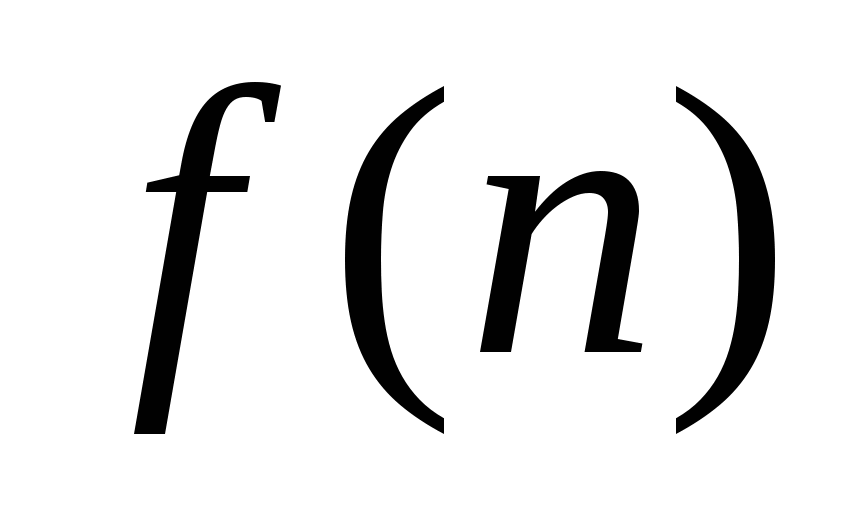 от длины входа от длины входа 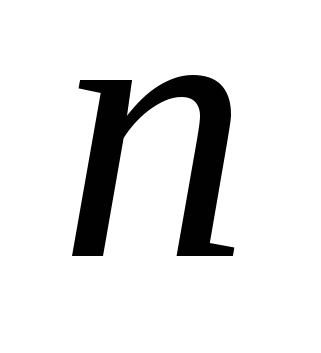 . Формула для описания функции . Формула для описания функции 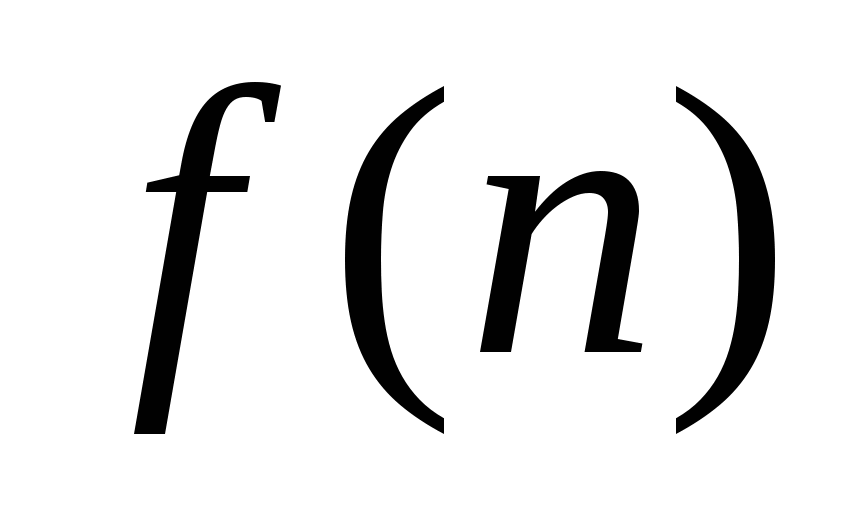 может быть достаточно сложной, разные составляющие этой формулы по-разному влияют на скорость ее роста. Элемент, который определяет поведение формулы, называется ее главным членом. Для больших значений может быть достаточно сложной, разные составляющие этой формулы по-разному влияют на скорость ее роста. Элемент, который определяет поведение формулы, называется ее главным членом. Для больших значений 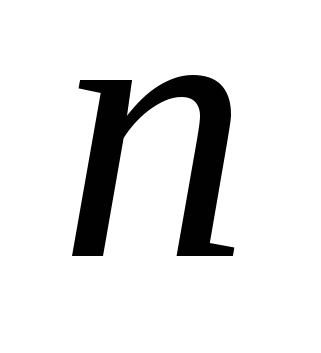 доминирует эффект главного члена, для малых доминирует эффект главного члена, для малых 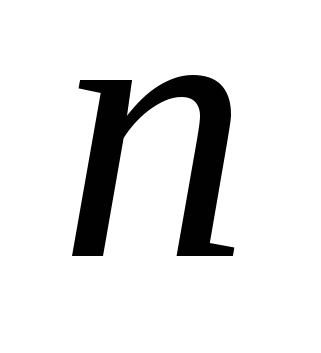 начинают оказывать влияние другие факторы, поэтому сравнение алгоритмов становится более сложным, и обычно достаточно иметь упрощенный вариант формулы для того чтобы понять ее поведение при возрастании ее аргумента. Учет только главного члена позволяет разбивать множество функций на классы эквивалентности, вводить иерархии на классах функций, и тем самым сравнивать множества задач по сложности их решения. начинают оказывать влияние другие факторы, поэтому сравнение алгоритмов становится более сложным, и обычно достаточно иметь упрощенный вариант формулы для того чтобы понять ее поведение при возрастании ее аргумента. Учет только главного члена позволяет разбивать множество функций на классы эквивалентности, вводить иерархии на классах функций, и тем самым сравнивать множества задач по сложности их решения.
Для описания асимптотических оценок имеется система нотаций:
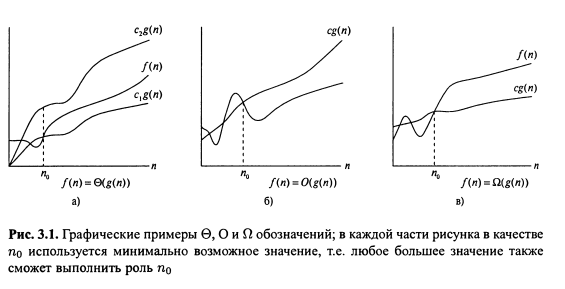
Говорят, что f(n)=O(g(n)), если существует такая константа c>0 и такое число n0, что выполняется условие 0≤f(n)≤c*g(n) для всех n≥n0. Более формально:

O(g(n)) используется для указания функций, которые не более чем в постоянное число раз не превосходятg(n), этот вариант используется для описания оценок сверху (в смысле «не хуже чем»).
Говорят, что f(n)=(g(n)), если существует такая константа c>0 и такое число n0, что выполняется условие 0≤c*g(n)≤f(n) для всех n≥n0. Более формально:

(g(n)) используется для указания функций, которые не менее чем в постоянное число раз превосходят g(n), этот вариант необходим для описания оценок снизу (в смысле «не лучше чем»).
Следующее определение объединяет предыдущие случаи:
Говорят, что f(n)=(g(n)), если найдутся такие константы c1,c2>0 и такое число n0, что для всех n≥n0 выполняется условие 0≤c1*g(n)≤f(n)≤c2*g(n). В этом случае, говорят - функция g(n) является асимптотически точной оценкой для f(n).
(g(n)) используется для указания функций того же порядка, что и g(n), этот вариант используется для описания асимптотически точных оценок.
Асимптотические сравнения обладают некоторыми свойствами отношений действительных чисел:
Транзитивность
Из f(n)=(g(n)) и g(n)=(h(n)) следует f(n)=(h(n)).
Из f(n)=O(g(n)) и g(n)=O (h(n)) следует f(n)=O(h(n)).
Из f(n) = (g(n)) и g(n) =(h(n)) следует f(n) =(h(n)).
Рефликсивность
Из f(n)=(f(n)).
Из f(n)=O(f(n)).
Из f(n) = (f(n)).
Симметричность
f(n)=(g(n)) справедливо тогда и только тогда, когда g(n)=(f(n)).
Перестановочная симметрия
f(n)=O(g(n)) справедливо тогда и только тогда, когда g(n)=(f(n))
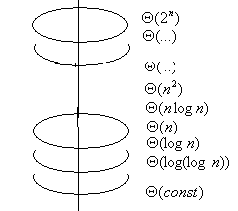
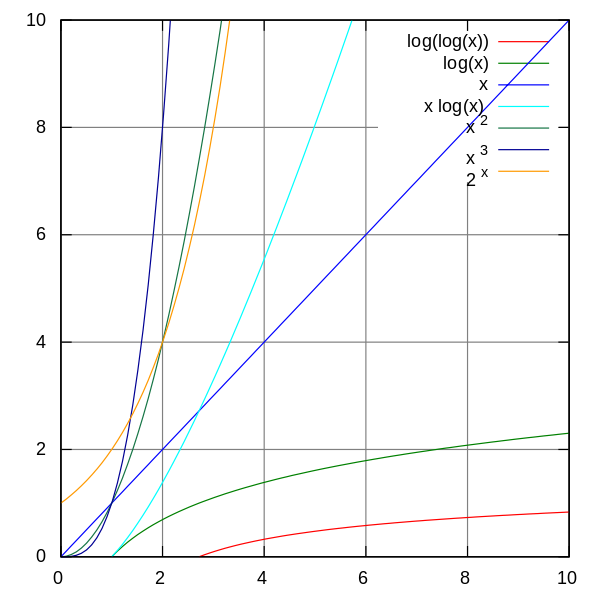
Как ведут себя значения приведенных выше функций в зависимости от размера решаемых задач демонстрирует таблица
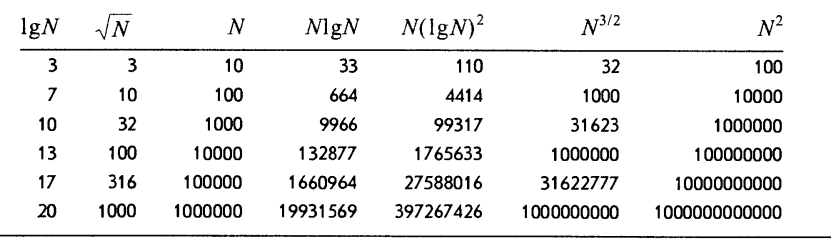
В зависимости от асимптотической функции времени решения может быть рассчитан размер задач, решаемых с такой скоростью.

Границы размера задач, определяемых скоростью роста сложности
Несмотря на то, что основное внимание здесь уделяется порядку роста величин, надо понимать, что большой порядок роста сложности алгоритма может иметь меньшую мультипликативную постоянную, чем малый порядок роста сложности другого алгоритма. В таком случае алгоритм с быстро растущей сложностью может оказаться предпочтительнее для задач с малым размером — возможно, даже для всех задач, которые нас интересуют.Например, предположим, что временные сложности алгоритмов 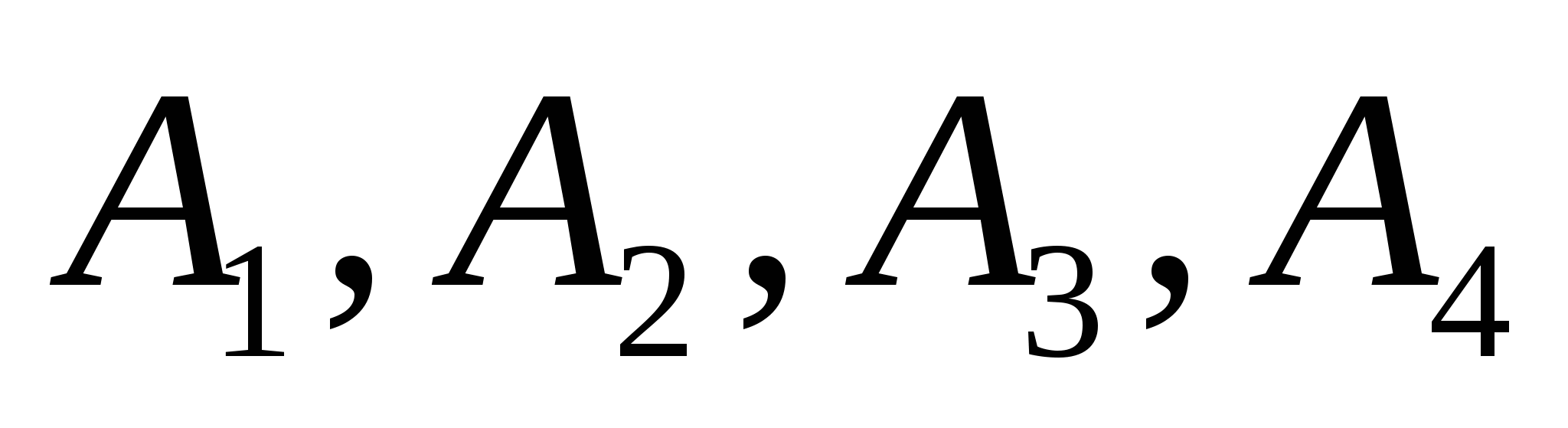 и и  в действительности равны соответственно 1000n, 100n log n, 10 в действительности равны соответственно 1000n, 100n log n, 10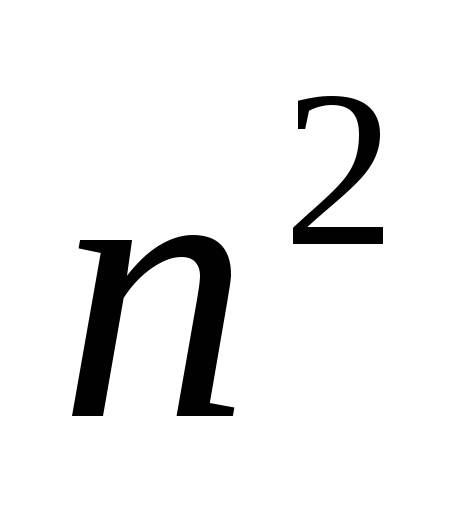 , , 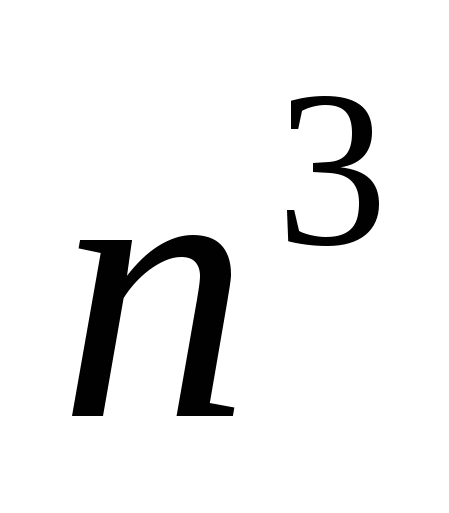 и 2". Тогда и 2". Тогда  будет наилучшим для задач размера будет наилучшим для задач размера 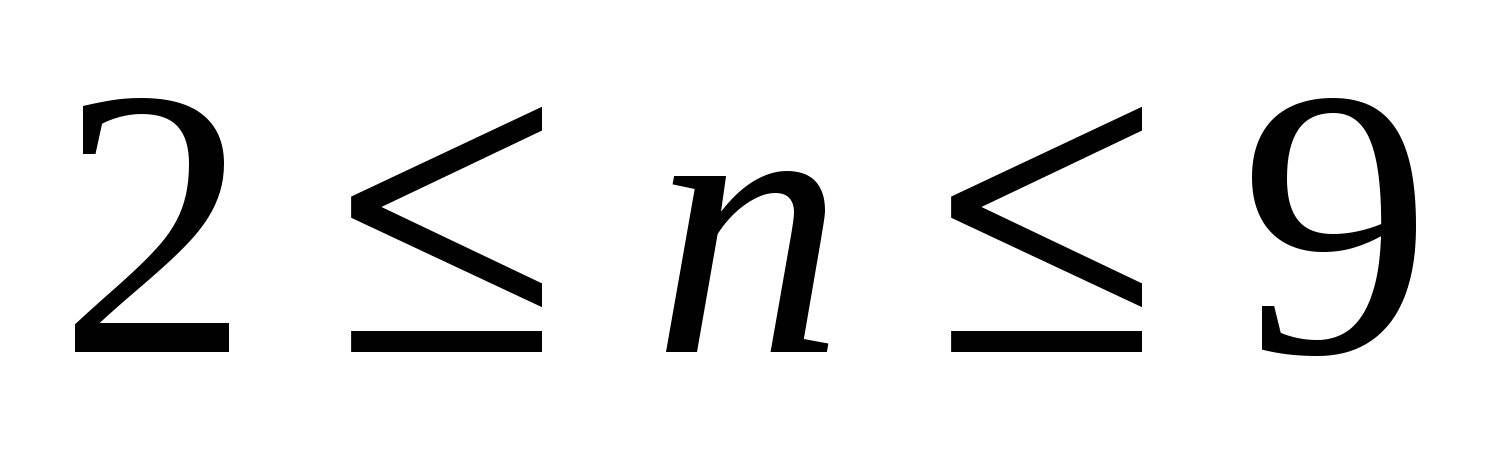 , ,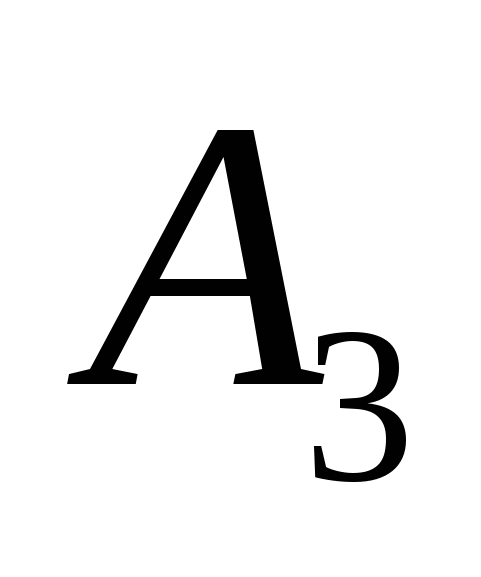 —для задач размера —для задач размера 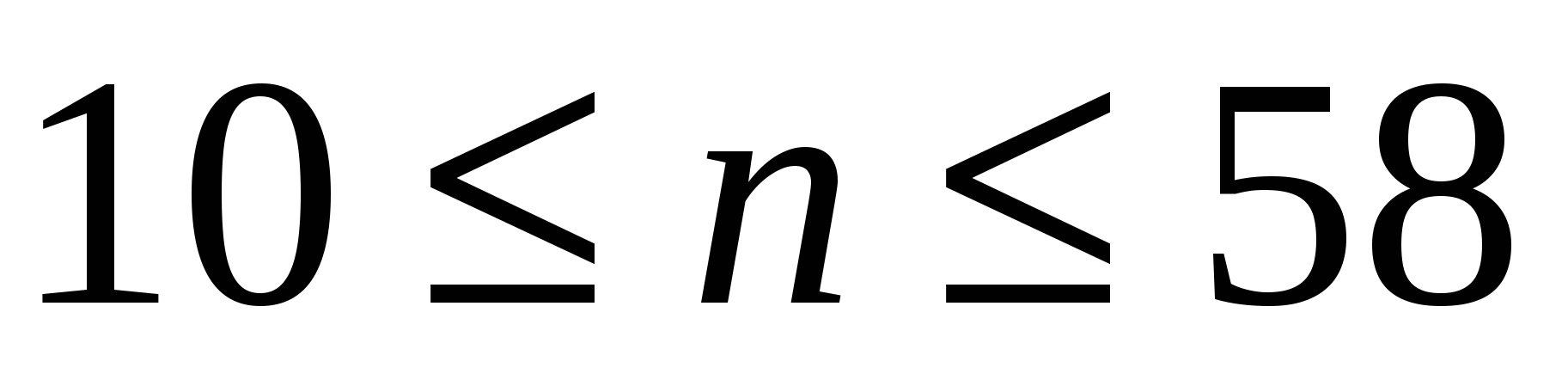 , ,  —при —при 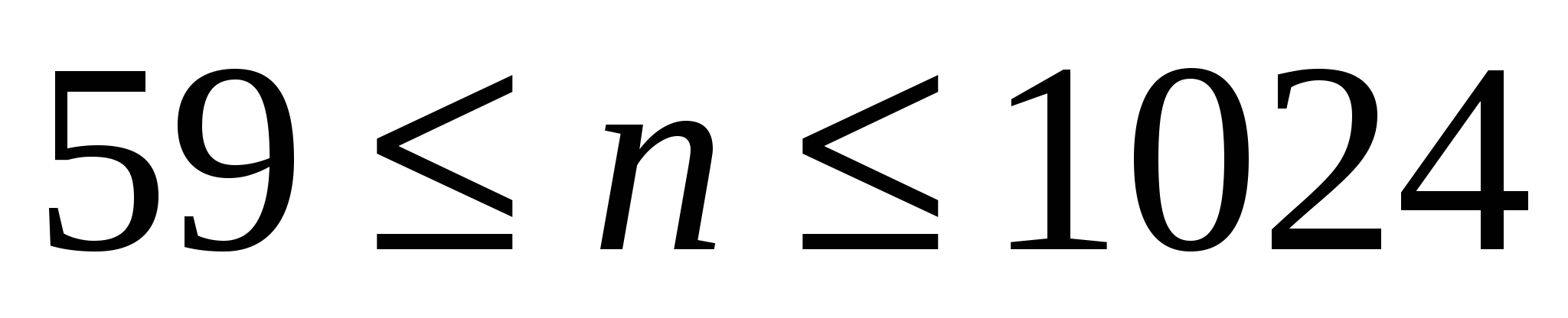 , а , а  — при n>1024. — при n>1024.
|
|
|
 Скачать 2.32 Mb.
Скачать 2.32 Mb.