Метод_указания к Лабораторным работам (1). Структурную и функциональную классификацию вс
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
|
Подготовка к лабораторной работе Данная лабораторная работа рассчитана на 3 часа работы в лаборатории и 2 часа работы дома. Она состоит в изучении методов информационного поиска массивов документов, заиндексированных с помощью различных ИПЯ, создание блок-схемы (согласно варианту), программы и получении конечных результатов. Для допуска к лабораторной работе необходимо изучить следующее вопросы: методы информационного пояска; методы организации ИПМ; индексирование документов и виды ИПЯ; необходимо составить блок-схему и ответить на контрольные вопросы к теоретической части. Содержание отчета 1. Цель и содержание работы. 2. Блок-схема и описание алгоритма. 3. Программа. 4. Результат работы программы. Контрольные вопросы 1. Вида условий поиска. 2. Основные методы поиска. 3. Методы организации информационно-поисковых массивов. 4. Что такое активный массив документов? 5. Что такое пассивный массив документов? 6. Дайте определение прямого и инверсного способа организации ИПМ. Их преимущества и недостатки? 7. Виды ИПЯ. 8. 0сновные виды я правила индексирования документов. 9. Что называется поисковым образом запроса (ПОЗ)? 10. Что называется поисковым образом документа (ПОД)? 11. Рассказать о двух этапах процесса информационного поиска. Приложение Содержание работы Индивидуальные задания Для поиска по условию А информационно-поисковым языком В, из раздела С, где Α, Β, С выбираются из таблицы согласно варианту.
Блок-схема и листинг программы информационного поиска по совпадению, по полному массиву документов, из раздела черчения (рис.1) Шаг 1. Чтение и печать массивов GOST (1,15) и nazv (1,15) (блок 2). Шаг 2. Ввод значения запроса S (блок 3). Шаг 3. Просмотр всех индексов, имеющихся в массиве GOST для нахождения значения, совпадающих с запросом S (блок 4) Шаг 4. Если индекс из массива GOST совпадает с запросом S, то из массива NAZV печатается документ, находящийся по адресу, указанному в массиве GOST, иначе переходим к просмотру следующего индекса (блоки 5,6) Шаг 5. По окончании цикла выходим на конец программы (блок 7) GOST - массив ГОСТов. NAZV - массив названий ГОСТов, представляет собой совокупность 15-ти символьных переменных длиной не более 30-ти символов. 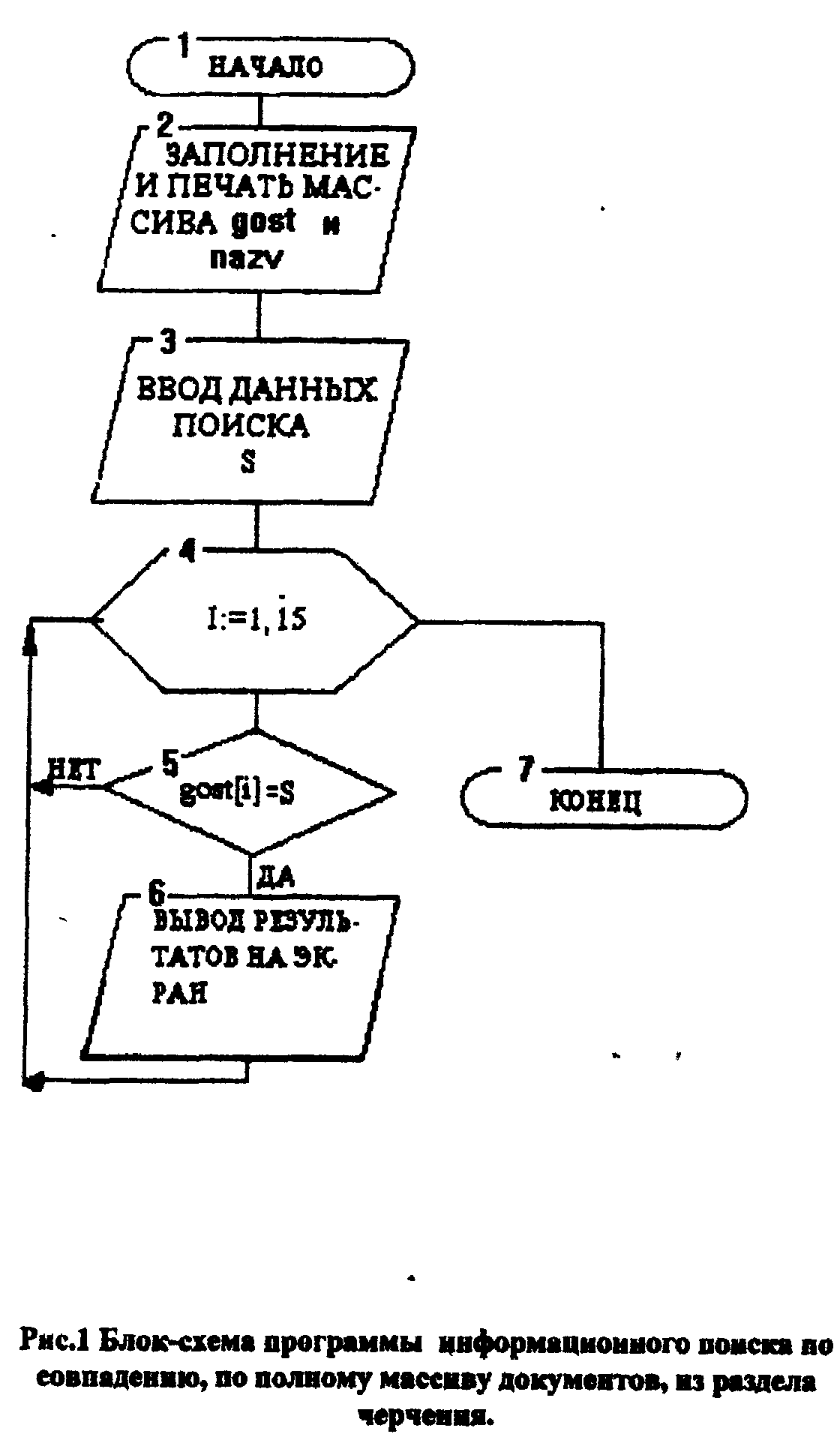 ТЕКСТ ПРОГРАММЫ program cherchenie; uses crt; const g:array[1..15] of string[30]= ('ГОСТ 6942.07-80','ГОСТ 6942.09-80', 'ГОСТ 6942.10-80','ГОСТ 6942.11-80', 'ГОСТ 6942.12-80','ГОСТ 6942.13-80', 'ГОСТ 6942.14-80','ГОСТ 6942.15-80', 'ГОСТ 6942.16-80','ГОСТ 6942.17-80', 'ГОСТ 6942.18-80','ГОСТ 6942.20-80', 'ГОСТ 6942.21-80','ГОСТ 6942.22-80', 'ГОСТ 6942.23-80'); n:array[1..15] of string[30]= ('Колено' ,'Отвод 110', 'Отвод-тройник приборный' ,'Отступ с раструбом', 'Прямые 90' ,'Прямые коменсационные', 'Прямые низкие' ,'Прямые переходные', 'Прямые переходные низхие' ,'Косые', 'Прямые' ,'Косые 45', 'Крестовина двух плоскостная','Муфта', 'Надвижные'); var gost:array[1..15] of string[30]; nazv:array[1..15] of string[30]; s:string[20]; b,i:integer; c,ch:char; begin clrscr; b:=0; {Чтение массива} for i:=1 to 15 do begin gost[i]:=g[i]; nazv[i]:=n[i]; end; gotoxy(10,4); write(' ГОСТ НАЗВАНИЕ'); {Печать исходного массива}; for i:=1 to 15 do begin gotoxy(8,6+i); write(gost[i]); gotoxy(40,6+i); write(nazv[i]); end; ch:=readkey; clrscr; {Ввод значения запроса }; gotoxy(28,12); write('ВВЕДИТЕ ИНФОРМАЦИЮ'); gotoxy(28,14); write('ДЛЯ ОСУЩЕСТВЛЕНИЯ'); gotoxy(32,16); write('ПОИСКА'); gotoxy(30,18); read(s); clrscr; gotoxy(10,4); write(' ГОСТ НАЗВАНИЕ'); {Вывод документа соответствующего запросу}; for i:=1 to 15 do begin if(s=gost[i]) or (s=nazv[i]) then begin b:=b+1; gotoxy(8,6+b); write(gost[i]); gotoxy(40,6+b); write(nazv[i]); end; end; ch:=readkey; end. Тестирование ГОСТ НАЗВАНИЕ ГОСТ 6942.07-80 Колено ГОСТ 6942.09-80 Отвод 110 ГОСТ 6942.10-80 Отвод-тройник приборный ГОСТ 6942.11-80 Отступ с раструбом ГОСТ 6942.12-80 Прямые 90 ГОСТ 6942.13-80 Прямые коменсационные ГОСТ 6942.14-80 Прямые низкие ГОСТ 6942.15-80 Прямые переходные ГОСТ 6942.16-80 Прямые переходные низхие ГОСТ 6942.17-80 Косые ГОСТ 6942.18-80 Прямые ГОСТ 6942.20-80 Косые 45 ГОСТ 6942.21-80 Крестовина двух плоскостная ГОСТ 6942.22-80 Муфта ГОСТ 6942.23-80 Надвижные ВВЕДИТЕ ИФОРМАЦИЮ ДЛЯ ОСУЩЕСТВЛЕНИЯ ПОИСКА ГОСТ 6942.22-80 ГОСТ НАЗВАНИЕ ГОСТ 6942.22-80 Муфта ЛАБОРАТОРНАЯ РАБОТА №1 Тема: "ИССЛЕДОВАНИЕ ПОМЕХОЗАЩИЩЕННОГО КОДИРОВАНИЯ. ОСНОВНЫЕ ПОНЯТИЯ ПОМЕХОЗАЩИЩЁННОГО КОДИРОВАНИЯ" Цель работы – освоить некоторые базовые понятия из предметных областей "передача и хранение информации" и "помехозащищённое кодирование", необходимые для дальнейшего изучения материалов по тематике. 1. Введение в помехозащищенное кодирование Объектом исследования, будет являться линия связи (линия передачи данных), безотносительно к тому, какие данные по ней передаются. Единственным допущением является то, что в указаниях предполагается представление данных в двоичном коде. Данные хранятся и обрабатываются на ЭВМ в виде последовательности кодовых комбинаций. Каждая из кодовых комбинаций представляет из себя двоичное число, представляющее то или иное информационное значение, которое может быть как числовым значением, так и – нечисловым (например - двоичным кодом символа). В таком же виде данные и передаются по линии передачи данных - в виде последовательности отдельных кодовых комбинаций. Линия передачи может быть представлена: 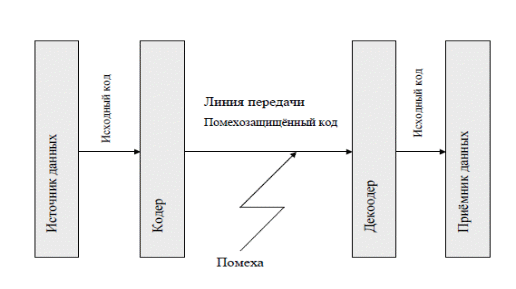 Следует иметь в виду, что процессы записи и считывания данных на устройствах хранения данных, также можно рассматривать как процесс передачи данных. В данном случае устройство записывающее данные на носитель – будет рассматриваться как передатчик данных, устройство считывающее данные – как приёмник данных, процесс хранения данных – как передача данных по линию связи. На линии связи могут иметь место помехи. Помехи могут вызвать изменение отдельных бит передаваемого сообщения (исказить данные, или другими словами – внести в них ошибки). Обычное кодирование (не имеющее помехозащищённых свойств, какое зачастую используются при хранении и обработке данных на ЭВМ) позволяет хранить данные компактно и обрабатывать быстро, но, увы, не позволяют, ни выявить факт возникновения ошибок (искажений) при передаче данных, ни, тем более, исправить данные полученные с искажениями (ошибками передачи). Помехозащищённое кодирование предполагает использование при передаче, на время передачи, вместо обычных – специальных, так называемых "помехозащищённых кодов". Эти коды не удобны для обработки данных (потому обработка данных "внутри" ЭВМ проводится в обычных кодах, не имеющих помехозащищённых свойств), но зато обладают свойствами очень полезными – при передаче данных, уникальными свойствами (с точки понимания иных людей не знакомых с тонкостями математики, свойствами как бы не "волшебными"). А именно: позволяют приёмнику (а точнее декодеру приёмника) заметить что часть полученных данных в процессе передачи была искажена, или даже позволяют исправлять ошибки передачи (восстанавливать исходную информацию, ту, что изначально посылалась на линию связи источником данных, что была до искажения). Помехозащишённое кодирование призвано повысить надёжность передачи сообщений, защитить получателя информации от получения искажённых данных (ещё говорят "организовать контроль данных при передаче"). С их использованием, процесс передачи данных выглядит следующим образом: 1) Перед началом передачи данных по линии связи, не имеющие помехозащищённых свойств обычные коды (принято называть "исходными") – заменяются на коды помехозащищённые. Каждый из кодов составляющих исходную исходной последовательности данных, индивидуально заменяется на соответствующий ему специальный "помехозащищённый код"; 2) Данные по линии связи передаются уже в помехозащищённых кодах; 3) А далее, если при передаче произойдёт искажение данных, в искажённых данных принятых приёмником, декодером помехозащищённго кодирования будут выявлены, а возможно даже и исправлены ошибки передачи. В заключение декодером будет произведена обратная замена, т.е. временно использовавшиеся для передачи помехозащищённые кодов, будут заменены на обычные (исходные) коды. Известно множество алгоритмов (или говорят "кодов") помехозащищенного кодирования. В зависимости от решаемой кодированием задачи, коды классифицируются: 1. Обнаруживающие – их применение позволяет приёмнику зафиксировать факт наличия ошибок в сообщении, но не определить номера ошибочных разрядов, а значит, такие коды - неспособны исправить ошибку. (Полезность таких кодов состоит в том, что в случае если факт наличия ошибки установлен - приёмник может запросить повторную передачу данных.) 2. Корректирующие – способны определить номера ошибочных разрядов и значит, способны исправить ошибку. 3. Обнаруживающе-корректирующие – в зависимости от числа ошибок в сообщении приёмник может исправить ошибку (при малом числе ошибок), или только зафиксировать факт возникновения ошибки (при большом числе ошибок). Уточним используемую при описании помехозащищённого кодирования терминологию, а также отметим некоторые ранее опущенные подробности. Помехозащишенное кодирование предполагает: 1. Наличие на стороне приёмника "кодера". Кодер – устройства или программа, заменяющая (в соответствии с использованным "алгоритмом кодирования") стандартные, или так называемые "исходные кодовые комбинации" (не позволяющие обнаруживать в них ошибки передачи), на так называемые "защищённые кодовые комбинации", обладающие так называемыми "помехозащишёнными свойствами" (то есть, позволяющие обнаруживать или даже исправлять появившиеся в процессе передачи ошибки). 2. Наличие на стороне приёмника "декодера". Декодер – устройство или программа, в соответствии с "алгоритмом декодирования" - анализирующая принятые защищенные кодовые комбинации, обнаруживающая или исправляющая ошибочные разряды, если они имеют место быть в принятой с линии передачи данных защищенных кодовых комбинациях, и затем, в завершении работы, вновь заменяющая защищённые кодовые комбинации на соответствующие им исходные кодовые комбинации. 2. Помехозашищённые свойства кода Возможности помехозащищённых кодов не беспредельны. При искажении слишком большого числа бит кодовой комбинации (превышающем так называемые "помехозащищённые свойства" помехозащищённого кода), декодер не срабатывает должным образом, оказывается не в состоянии корректно обнаружить и исправить возникшие при передаче ошибки. Степень искажения данных при передаче характеризуется числовым параметром: Кратность ошибки (k) - число разрядов кодовой комбинации, исказившихся в процессе передаче данной кодовой комбинации. Помехозащищённые свойства, любого из алгоритмов помехазащищенного кодирования, характеризуются двумя числовыми параметрами: Максимальной кратностью обнаруживаемой ошибки (kо) – то максимальное значение кратности ошибки k при которой данный алгоритм ещё способен гарантировать обнаружение факта наличия ошибки независимо от того, какие именно разряды в комбинации искажены. Таким образом: при возникновении ошибки кратностью k < kо - ошибка будет гарантировано обнаружена, при k > kо - данным алгоритмом обнаружение ошибки не гарантировано. Максимальной кратностью корректируемой ошибки (kк) – то максимальное значение кратности ошибки k при которой данный алгоритм ещё способен гарантировать исправление (коррекцию) ошибки независимо от того, какие именно разряды в комбинации искажены. При возникновении ошибки кратностью k < kк - ошибка будет откорректирована, при k > kк - коррекция ошибки не гарантирована, в зависимости от того в каких именно разрядах произошла ошибка, результат работы алгоритма декодирования может быть разным, и непредсказуем. А именно: декодер, возможно – не заметит факт наличия ошибок, возможно – заметит, но пытаясь откорректировать ошибку неправильно определит какие именно разряды искажены. Таким образом, имеем: 1) Для кодов не имеющих помехозащищённых свойств, справедливо: kо = 0, kк = 0 2) Для обнаруживающих помехозащищённых кодов справедливо: kо > 0, kк = 0 3) Для корректирующих помехозащищённых кодов справедливо: : kо > 0, kк > 0, kо = kк (при кратности ошибки k < kк ошибка исправляется корректно, при большей кратности ошибки результат работы декодера непредсказуем) 4) Для обнаруживающее-корректирующих помехозащищённых кодов справедливо: kо > 0, kк > 0, kо > kк (при кратности ошибки k < kк ошибка корректируется, при кратности ошибки большей kк но ещё не превышающей kо ошибка - будет обнаружена, но декодер "заметит" что кратность ошибки слишком высока для коррекции и откажется от попытки коррекции (вместо этого передатчику будет передан "запрос на повторную передачу данных", т. е. просьба повторить передачу искажённые данные заново), и только если k > kо - результат работы декодера окажется непредсказуемым (см. выше). 3. Некоторые понятия из теории кодов Для того чтобы не только понять, для чего нужны помехозащищённые коды, но и понять как они работают, нам потребуется узнать некоторые, возможно новые для вас, понятия теории кодирования информации. Прежде всего такие важные для помехозащищённого кодирования понятия как "кодовое расстояние" и "минимальное кодовое расстояние". Кодовое расстояние (dij) – вычисляется между кодами одинаковой длинны, и равно числу разрядов в которых эти два кода отличаются. Пример: Пусть кодовые комбинации К(1) = 00110011, К(2) = 00111100 Тогда кодовое расстояние: d12 = 4 Обратим внимание: чтобы при искажении один код K(i), превратился в другой K(j), необходимо чтобы были искажены никак не менее чем dij разрядов. Минимальное кодовое расстояние (dmin) – вычисляется в группе из множества кодов одинаковой длинны, и равно минимальному из кодовых расстояний взятых между двумя произвольными кодовыми комбинациями из группы. Пример: Пусть кодовые комбинации К(1) = 0000, К(2) = 1111, К(3) = 0001 Тогда: Кодовые расстояния: d12 = 4, d13 = 1, d23 = 3 Минимальное кодовое расстояние: dmin = 1 Обратим внимание: чтобы при искажении любого кода из группы он превратился в другой код из группы, необходимо чтобы были искажены не менее dmin разрядов. Далее познакомимся с такими, связанными между собой понятиями, как "алфавит источника сообщения", "число возможных состояний кода", а также понятиями "безъизбыточный код" и "избыточный код". Сообщение строятся с использованием некого набора символов. Например, тексты состоит из последовательности символов, каждый из которых представляет один из символов алфавита (знаки препинания и прочие знаки, используемые в текстах также будем считать "элементами алфавита"). Число "элементов алфавита" в используемом алфавите, называют "размером алфавита источника сообщения", или, что менее точно но зато короче "алфавитом источника сообщения", алфавит источника сообщения принято обозначать буквой М (а именно М заглавной, большой). Например, если при составлении текста на русском сообщения использовать исключительно только прописные символы кириллицы, тогда M = 33. Сообщения могут быть не только текстовыми, но, какова бы не была информация, сообщения строятся из какогото ограниченного набора символов, буквенных ли, числовых ли (каждое число тоже можно рассматривать как символ), каких других, число используемых символов может быть очень большим, но в любом случае это число (М – "алфавит источника сообщения") ограничено. Как известно в ЭВМ информация храниться не в виде символов, в виде двоичных чисел (или по иному это называется в виде "двоичных кодов"). Двоичные коды заменяют символы, замена производится в соответствии с принятой "кодовой таблицей". В соответствии с таблицей каждому элементу алфавита ставится в соответствие свой "двоичный код". "Длинной двоичного кода" называется число двоичных бит, составляющих код. Длину кода будем обозначать буквой n (а именно n малой, прописной). От длинны кода зависит число состояний, которое может принимать код, оно же "число возможных состояний кода", его принято обозначать буквой N (а именно N большой, заглавной). Для двоичного кода длинны n, число возможных кодовых комбинаций равно N=2n . Обычно длинна всех кодов составляющих сообщение, используемых при кодировании сообщения – одинакова. Пусть, например, нам нужно закодировать в двоичные коды текст с алфавитом источника сообщения М=32. В этом случае, двоичные коды какой длинны мы можем использовать при кодировании? Ответ – коды длинной не менее 5 бит (25 = 32). Меньшего числа бит просто не хватит, что бы каждому символу алфавита поставить в соответствие своё, уникальное двоичное число (двоичный код), а вот пятибитовые коды, в данном случае, будут как бы "как раз". По науке такое кодирование называют "безъизбыточным кодированием" (или "безъизбыточным кодом"), для такого кодирования характерно M=N. Для каждого символа свой код, никаких "лишних" кодов, что не используются для кодирования символов – нет, быть не может. Далеко не всегда используемое кодирование является "безъизбыточным". Например в нашем случае (М=32) при двоичном кодировании также могут быть использованы коды длиной n более 5, например шестиразрядный (для него N=64), семиразрядный (N=128) и так далее. Такое кодирование (когда используются коды с N>M) называют "избыточным кодированием", или "избыточным кодом". Вообще говоря, избыточное кодирование имеет тот недостаток что закодированное сообщение получается менее компактным, более длинным чем могло бы быть при безъизбыточном кодировании, но иногда избыточное кодирование неизбежно (что, например, делать если М=35?), а иногда даже и полезно. Например, именно специальным (и правильным, грамотным) образом организованное избыточное кодирование, позволяет создавать "помехозащищённые коды" Задания 1) Пусть используется помехозащищенный код с характеристиками kо = 3, kк = 2. При передаче информации происходит ошибка кратностью а) k = 1; б) k = 3; в) k = 8; г) k = 4; д) k = 2. Определить результат применения данного кодирования в каждом из случаев. 2) Пусть кодовые комбинации образуют группу из следующих комбинаций: К(1) = 00001111, К(2) = 11110000, К(3) = 11111111, К(4) = 00000011. Определить минимальное кодовое расстояние между кодами группы. 3) Пусть минимальное кодовое расстояние в группе кодов равно dmin = 8. Сколько ошибок можно внести в любую из кодовых комбинаций из этой группы, чтобы можно было гарантировать, что она не превратится в какую либо другую комбинацию из этой же группы? 4) Подобрать три кодовые комбинации, минимальное кодовое расстояние между которыми, было бы : а) dмин = 2, б) dмин = 3, в) dмин = 4, г) dмин = 5. ЛАБОРАТОРНАЯ РАБОТА № 8 Тема: «Работа с множествами» Цель работы: изучение основ теории множеств, способов задания множеств, основных операций над множествами. 1.Основные понятия Теория множеств - математическая теория, которая лежит в основе большинства разделов математики. Основы теории множеств заложил в 1878-1884 гг. немецкий математик Г.Кантор. Множество есть собрание (набор, совокупность) элементов множества, причем понятие множества не подлежит логическому определению. Принадлежность элемента а множеству Μ обозначается а |
