Метод_указания к Лабораторным работам (1). Структурную и функциональную классификацию вс

Название	Структурную и функциональную классификацию вс
Дата	20.02.2022
Размер	2.03 Mb.
Формат файла
Имя файла	Метод_указания к Лабораторным работам (1).doc
Тип	Лабораторная работа #367797
страница	2 из 11

1 2 3 4 5 6 7 8 9 10 11

Шаг 1: Вводятся и печатаются исходные характеристические параметры α, β, γ, ε, δ, ξ (блок 2). Шаг 2: Вычисляются параметры FM (блок 3).

Шаг 3: Проверка условия FM = 901800900 и FB = 12. Если условие выполняется, то на печать выводится соответствующее значение (блок 4,5).

Шаг 4: Если предыдущее условие не выполняется, то проверяется следующее: FM = 1 и FB = О (блок 6). Если второе условие выполняется, то проверяется следующая информация (блок7).

Шаг 5: Если предыдущее условие не выполняется, то проверяется следующее: FM < 901800900 и 8 <= FB < 12 (блок 8).·Если данное условие выполняется, то на печать выводится соответствующая символьная информация (блок9). Читается конец программы (блок 11).

Шаг6: В противном случае так же выводится на печать соответствующая символьная информация (блок 10). Читается конец программы (блок 11)

Текст программы

#include

#include

#include

#include

main()

{ long p1, p2, p3, p4, p5, p6, fb,fm;

clrscr ();

printf("\n ВВЕДИТЕ ЗНАЧЕНИЯ ХАРАКТЕРИСТИЧЕСКИХ");

printf("\n ПАРАМЕТРОВ 'п");

scanf(" %d %d %d %d %d %d ", p1, p2, p3, p4, p5, p6);

fm=pow(2,p1)*pow(3,p2)*pow(5,p3)*pow(7,p4)*pow(11,p5)*pow(13,p6);

fb=p1+p2+p3+p4+p5+p6;

if ((fm=901800900) && (fb=12))

printf("\n АБСОЛЮТНО ЦЕНТРАЛИЗОВАННАЯ ВС '\n");

else

if((fm=1) && (fb=0))

printf("\n АБСОЛЮТНО ДЕЦЕНТРАЛИЗОВАННАЯ ВС '\n");

else

if ((fm < 901800900) && (fb < 12) && (fb>=8))

printf("\n ЦЕНТРАЛИЗОВАННАЯ ВС '\n");

else printf("\n ДЕЦЕНТРАЛИЗОВАННАЯ ВС '\n");}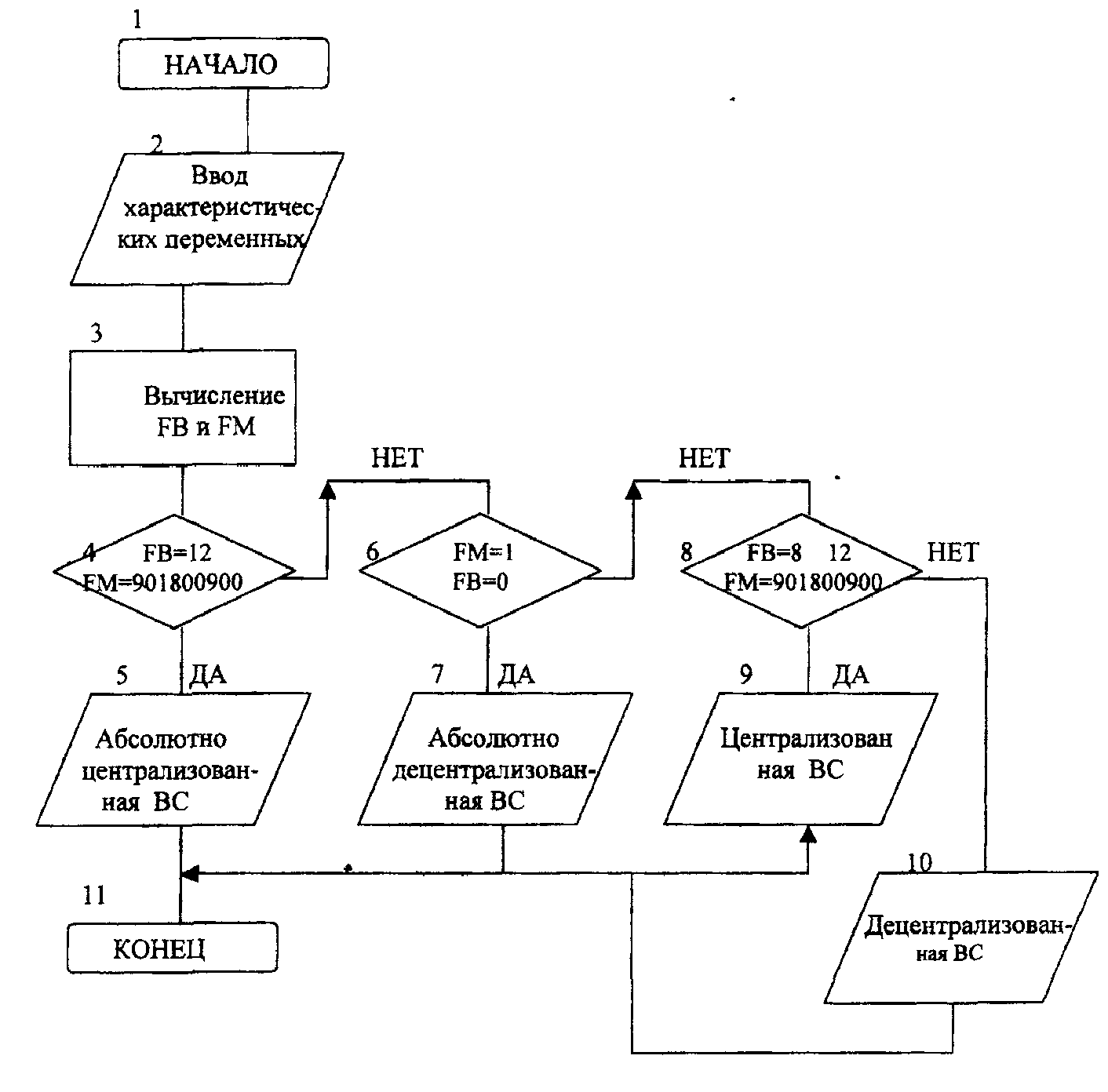

Рис. 7 Блок-схема алгоритма программы структурной классификации ВС по заданным характеристическим параметрам
Тестирование

Исходные данные						Вычисляемые		Структура
α	β		δ		ξ	F	F	ВС
2	2	2	2	2	2	12	901800900	АЦ

АЦ - абсолютно централизованные ВС.
Результаты выполнения программы:
Введите значения характеристических параметров

2 2 2 2 2 2

F_m=12 F_b=901800900

Абсолютно централизованная ВС

Исходные данные						Вычисляемые		Структура
α	β		δ		ξ	F	F	ВС
0	0	0	0	0	0	0	1	АДЦ

АДЦ - абсолютно децентрализованные ВС.
Результаты выполнения программы:
Введите значения характеристических параметров

0 0 0 0 0 0

F_m=0 F_b=l

Абсолютно децентрализованные ВС

Исходные данные						Вычисляемые		Структура
α	β		δ		ξ	F	F	ВС
2	2	2	2	1	1	10	11711700	ЦН

ЦН- централизованные ВС.
Результаты выполнения программы:
Введите значения характеристических параметров

2 2 2 2 1 1

F_m=10 F_b=11711700

Централизованная ВС

Исходные данные						Вычисляемые		Структура
α	β		δ		ξ	F	F	ВС
0	0	0	1	1	0	2	77	ДЦ

ДЦ - децентрализованные ВС.
Результаты выполнения программы:
Введите значения характеристических параметров

0 0 0 1 1 0

F_m=2 F_b=77

Децентрализованная ВС

ЗАДАНИЕ №2

Функциональная классификация по заданным характеристическим параметрам

Таблица №2

Номер варианта	Исходные данные												Вычисляемые Η
Номер варианта	λ	μ		π		θ	ψ			ξ	η		Вычисляемые Η
1	0	0	1	1	0	1	0	1	1	1	0	0	6
2	0	1	0	0	0	0	0	0	0	0	0	0	1
3	0	0	1	1	1	0	0	1	0	0	0	0	1
4	0	1	1	1	1	1	0	1	1	1	0	0	8
5	0	0	0	1	0	0	0	0	0	0	0	0	1
6	0	0	1	1	0	1	1	0	1	1	0	0	6
7	1	0	0	0	1	0	0	0	0	0	0	0	2
8	0	1	1	1	1	1	1	0	0	1	0	1	8
9	0	0	0	0	0	0	1	0	0	0	0	0	1
10	1	1	0	0	0	0	0	0	0	0	1	0	3
11	1	1	1	0	0	1	1	0	1	1	0	0	7
12	0	1	1	1	0	1	1	1	0	1	1	0	8
13	0	0	0	0	1	1	0	0	1	0	1	0	4
14	1	1	0	0	1	1	0	0	0	0	0	1	5
15	0	0	1	0	0	0	0	0	0	0	0	0	1
16	0	0	0	1	1	1	1	1	1	1	0	0	7
17	1	0	0	0	1	0	0	0	0	0	0	0	2
18	0	1	0	1	0	0	0	0	1	1	1	1	6
19	0	0	0	0	1	0	0	1	1	1	0	0	4
20	1	0	0	0	0	0	0	0	0	0	0	0	1
21	0	1	1	0	0	1	1	1	0	1	1	0	7
22	0	1	0	1	0	1	1	1	0	1	0	1	7
23	0	0	1	1	1	0	0	0	1	1	1	1	7
24	0	1	1	0	0	0	1	1	0	1	0	0	5
25	1	1	0	0	1	1	0	1	1	0	1	0	7

Η = 12, (максимальное значение) у существующих систем не достигнуто.

Н = 1, (минимальное значение) система имеет весьма малые функциональные возможности.

Η = 1...8, система имеет большие функциональные возможности.
Алгоритм решения

Шаг 1: Вводятся и печатаются исходные характеристические параметры λ, μ, ν, π, ρ, θ, ψ, φ, ε, ξ, η, ω (блок 2).

Шаг 2: Вычисляется параметр Н (блок 3).

Шаг 3: Проверка условия Н = 12 (блок 4). Если условие выполняется, то на печать выводится

соответствующее значение (блок 5) Читается конец программы (блок 10).

Шаг 4: Если первое условие не выполняется, то проверяется следующее: Н=1 (блок 6). Если второе условие выполняется, то на печать выводится соответствующая символьная информация (блок 7). Читается конец программы (блок 10).

Шаг 5: Если предыдущее условие не выполняется, то проверяется следующее: (Н>2) и (Н<=8)(блок8). Если данное условие выполняется, то на печать выводится соответствующая символьная информация (блок 9). Читается конец программы (блок 10).
Текст программы
program lab6;

uses crt;

var

p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,h:byte;

begin

clrscr;

writeln('ВВЕДИТЕ ЗНАЧЕНИЕ ХАРАКТЕРИСТИЧЕСКИХ');

writeln('ПЕРЕМЕННЫХ');

readln(p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12);

h:=p1+p2+p3+p4+p5+p6+p7+p8+p9+p10+p11+p12;

case h of

1:begin

writeln('МИНИМАЛЬНОЕ ЗНАЧЕНИЕ');

writeln('ВС ИМЕЕТ ВЕСЬМА МАЛЫЕ');

writeln('ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ');

end;

12:begin

writeln('МАКСИМАЛЬНОЕ ЗНАЧЕНИЕ');

writeln('У СУЩЕСТВУЮЩИХ ВС ПОКА НЕ');

writeln('ДОСТИГНУТО');

end;

2..8:begin

writeln('ВС ИМЕЕТ БОЛЬШИЕ ФУНКЦИОНАЛЬНЫЕ');

writeln('ВОЗМОЖНОСТИ');

end;

end;

end.

end.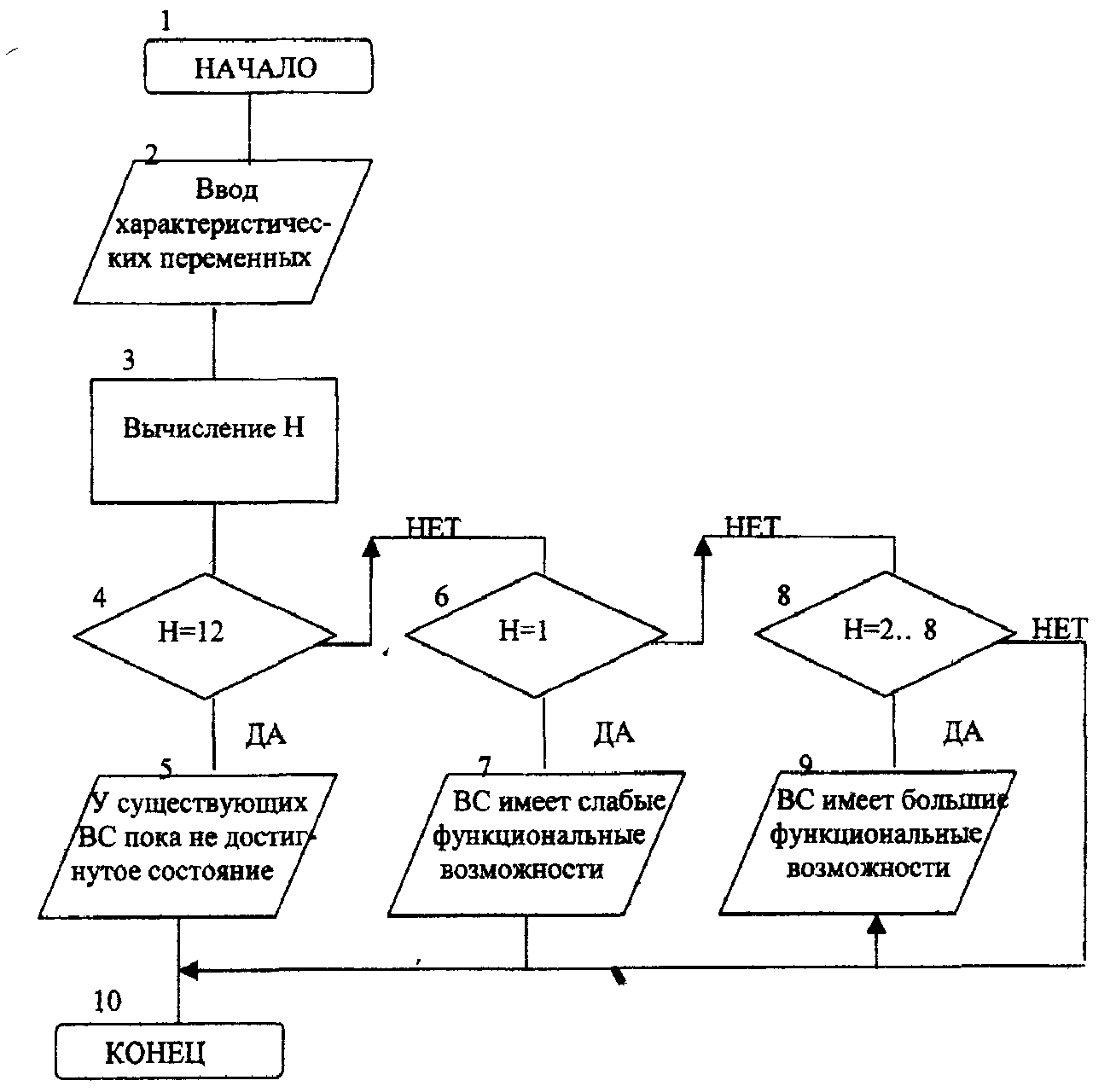

Рис. 8 Блок-схема алгоритма программы функциональной классификации ВС по заданным характеристическим параметрам.
Тестирование

Исходные данные												Вычисляемые
λ	μ	ν	π		θ	ψ	χ,			η		Η
0	1	0	0	0	0	0	0	0	0	0	0	1

Η = 1 (минимальное значение) система имеет весьма малые функциональные возможности.
Результаты выполнения программы:
Введите значения характеристических параметров

0 1 0 0 0 0 0 0 0 0 0 0

Н=1

Минимальное значение ВС имеет весьма малые функциональные возможности.

Исходные данные												Вычисляемые
λ	μ	ν	π		θ	ψ	χ,			η		Η
1	1	1	1	1	1	1	1	1	1	1	1	12

Η = 12 (максимальное значение) у существующих систем не достигнуто.
Результаты выполнения программы:
Введите значения характеристических параметров

1 1 1 1 1 1 1 1 1 1 1 1

Н=12

Максимальное значение у существующих ВС не достигнуто

Исходные данные												Вычисляемые
λ	μ	ν	π		θ	ψ	χ,			η		Η
1	0	0	1	1	1	1	0	0	1	0	0	6

Η = 6, система имеет большие функциональные возможности.
Результаты выполнения программы:
Введите значения характеристических параметров

1 0 0 1 1 1 1 0 0 1 0 0

Н=6

ВС имеет большие функциональные возможности.

ЛАБОРАТОРНАЯ РАБОТА № 2

Тема: «Разработка алгоритмов и программ для моделирования информационных подсистем»
ЦЕЛЬ РАБОТЫ: составление алгоритмов и программ для моделирования информационных подсистем.

1. Математическая модель технологии обработки информации
Рассмотрим технологический процесс обработки информации без ее накопления в месте обработки. На вход такого технологического процесса подается поток информационных документов (первичных информационных документов, вторичных информационных документов, запросов, заявок и т.п.). На выходе этого процесса получаются обработанные информационные документы (рис. 1.1). Плотность (интенсивность) потока информационных документов на входе обозначим (t), плотность потока обработанных информационных документов на выходе -_o(t).

Будем полагать, что в обработке информации принимает участие n статистически одинаковых каналов (операторов или технических устройств), каждый из которых имеет интенсивность обслуживания μ(t). Интенсивность обслуживания канала μ(t) будет равна интенсивности потока обработанных документов, если на входе этого канала обслуживания есть "очередь" необработанных документов. Необработанные информационные документы распределяются на обработку по всем n каналам. Если все n каналов заняты обработкой информации, то необработанные документы откладываются (становятся в очередь на обслуживание). Дисциплина очереди естественная: какие документы поступили раньше, те в первую очередь будут обработаны. Число мест в очереди на обработку практически не ограничено. Схема такой системы показана на рис. 1.2.

Состояния такой системы будем связывать с числом информационных документов, поступивших на обработку, но еще не обработанных.

x_о - в системе обработки информации нет информационных документов;

x₁ - в системе обработки информации имеется один информационный документ и он обрабатывается в одном из каналов.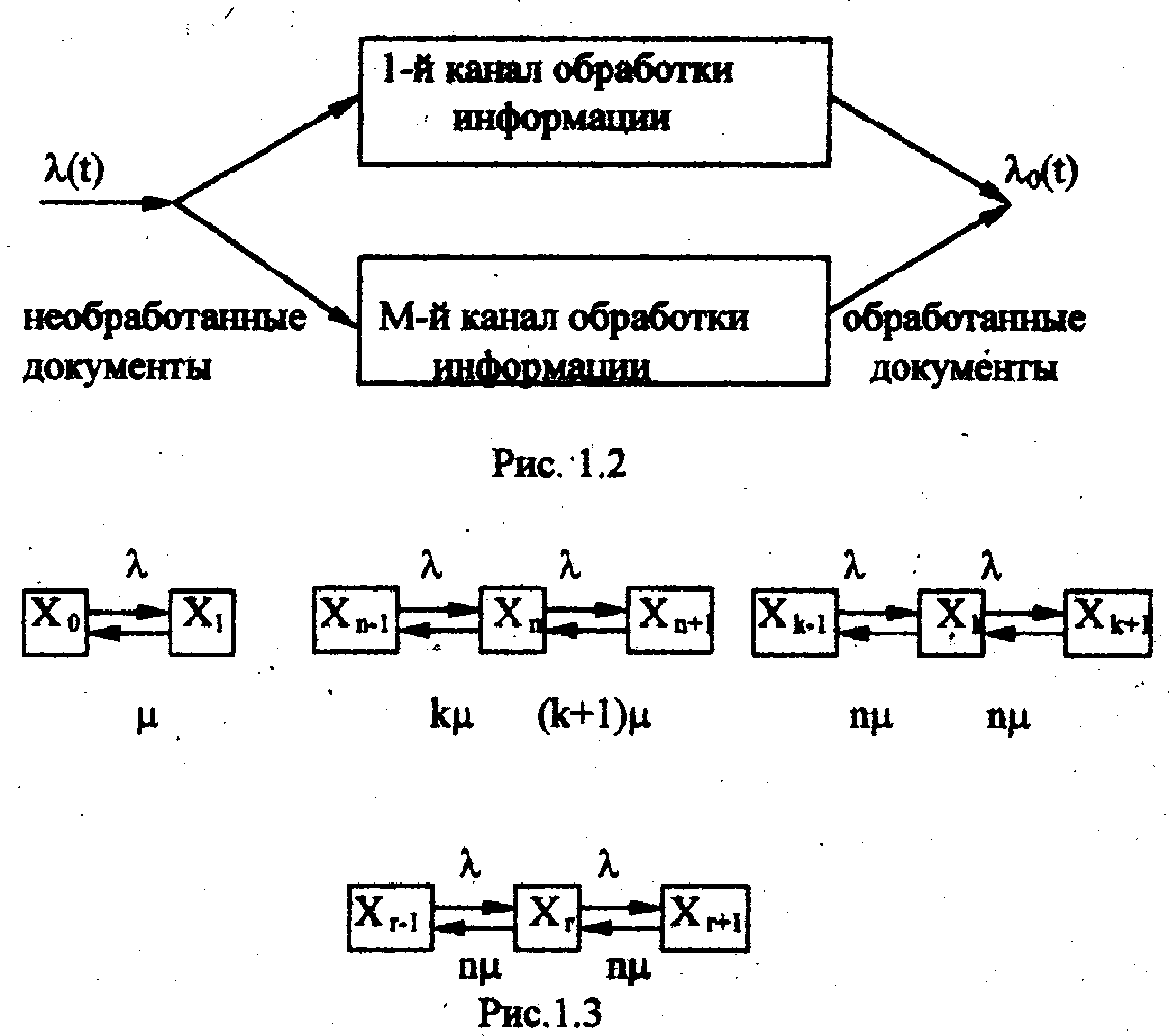

x_k - в системе обработки информации имеется k информационных документов (к
x_n - в системе обработки информации имеется n информационных, документов и все они обрабатываются в n каналах, очереди, необработанных документов нет;

x_n₊_r- в системе обработке информации имеется n+r информационных документов, n из которых обрабатываются в n каналах, а r находятся в очереди на обработку.

Размеченный граф состояний такой системы обработки информации показан на рис. 1.3. Для простоты зависимость интенсивностей (t) и (t) от времени t на рис. 1.3 и в дальнейшем опущена.

Многочисленные расчеты показывают, что в отношении этих систем можно сделать допущение о том, что входящий поток информационных документов и поток обработки этих документов в канале являются пуассоновскими.

Второе допущение состоит в том, что рассматривается только стационарный режим работы системы обработки информации. Другими словами, интенсивность потоков необработанных документов и интенсивность их обработки в каждом канале являются постоянными величинами: l=const и μ=const. Кроме того, временем переходного процесса в системе обработки информации пренебрегаем.

Стационарный режим работы системы обработки информации может существовать только при условии:

(1.1)

Откуда

(1.2)
Формула (1.1) указывает на то очевидное условие, что суммарная производительность (интенсивность) всех каналов обработки информации должна быть больше интенсивности входного потока подлежащих обработке информационных документов.

Вероятность того, что в системе обработки информации имеется k информационных документов, все они обрабатываются и очереди из необработанных документов нет: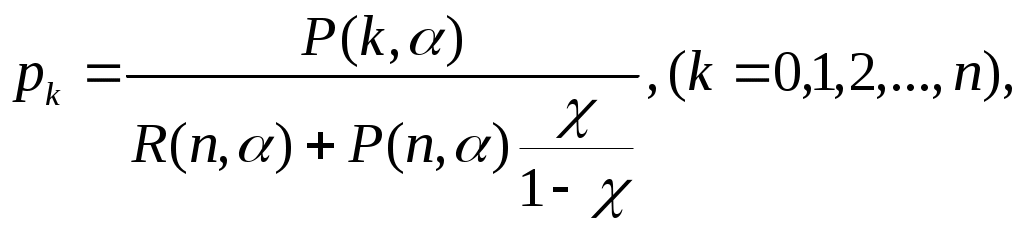

(1.3)

где,

;

; (1.4)

; (1.5)

. (1.6)
Вероятность того что в системе обработки информации имеется n+r информационных документов: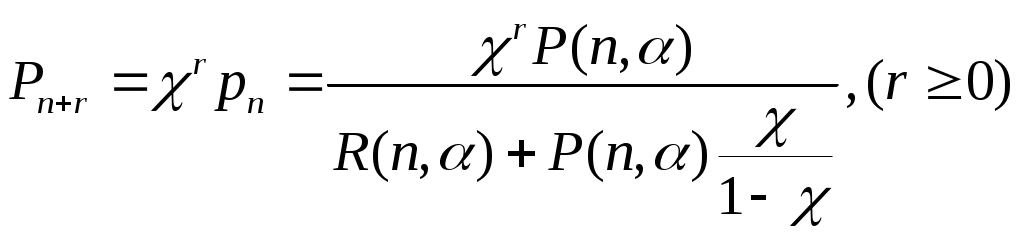

. (1.7)
Для рассматриваемой системы обработки информации вероятность того, что документ будет обработан (рано или поздно), равна единице. Следовательно, плотность потока обработанных документов в установившемся режиме будет равна плотности потока документов, поступающих на вход:

(1.8.)

Среднее число занятых каналов обработки информации (среднее число обрабатываемых документов) в данный (произвольный) момент времени t:

. (1.9)

Среднее число необработанных документов, находящихся в "очереди" на обработку:

. (1.10)

Иногда полезно знать дисперсию и среднее квадратическое отклонение числа документов, находящихся в "очереди" D_r и σ_r. Найдем второй начальный момент: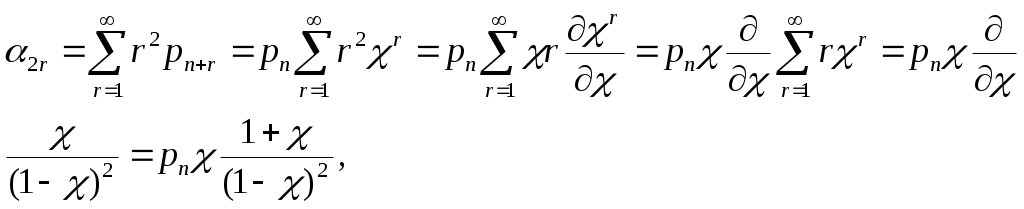

Откуда,

. (1.11)

Так как величина D_r>0, то средняя длина очереди не превышает величины:

Этим неравенством можно грубо оценивать длину очереди. Более полную оценку величины

можно получить из неравенства:

Среднее квадратическое отклонение будет равно:

. (1.12)

Среднее число документов, находящихся в системе обработки информации:

. (1.13)

Среднее время нахождения документа в очереди на обработку: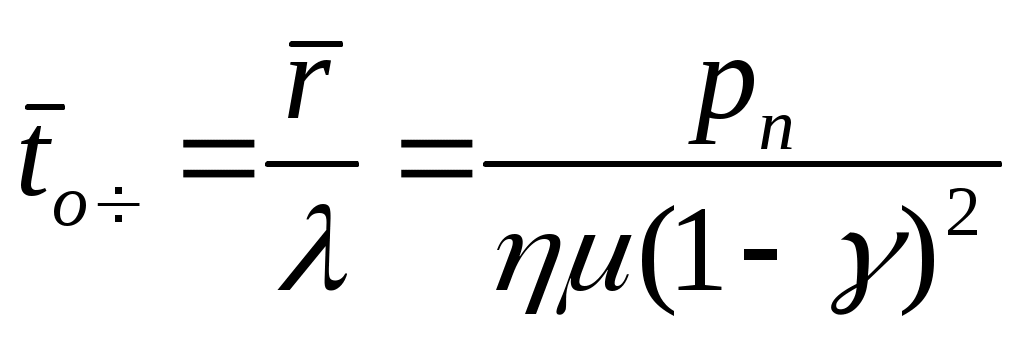

. (1.14)

Среднее время нахождения документа на обработке:

. (1.15)

Среднее время нахождения документа в системе обработки информации:

. (1.16)

Плотность распределения времени нахождения документа в «очереди» на обработку будет равна: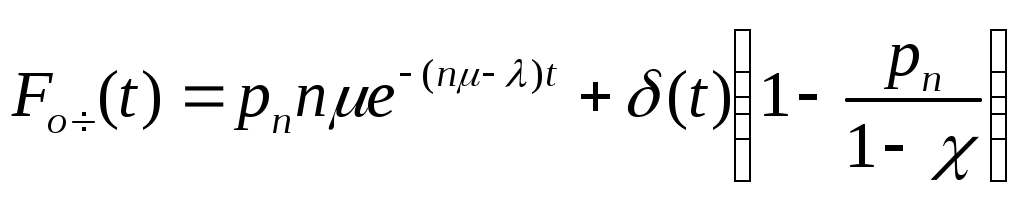

, (1.17)

где,

(t)-известная дельта функция.

Ф
, при t

0
, при t > 0
ункция распределения времени Т_оч нахождения документа в очереди на обработку будет равна: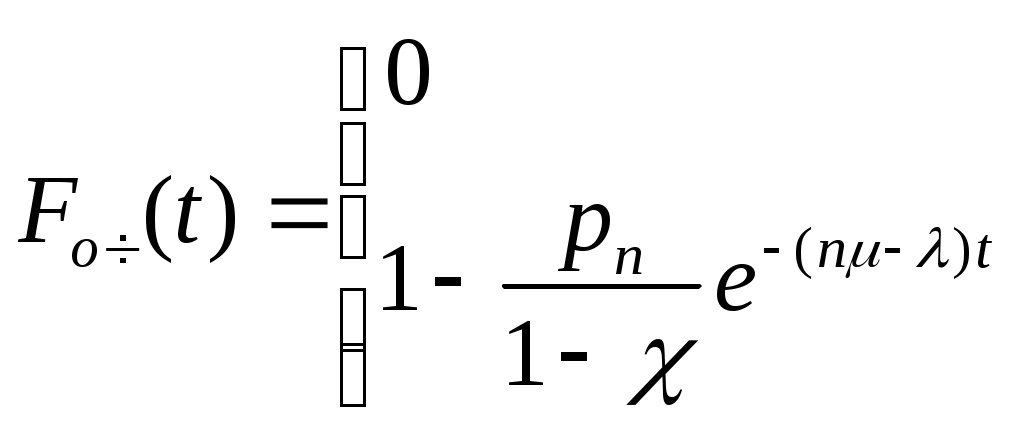

(1.18)
График этой функции показан на рис. 1.4. Величина Т_оч является случайной величиной смешанного типа, имеющей один скачёк при t=0. Величина этого скачка равна вероятности того, что в системе обработки информации нет очереди необработанных документов.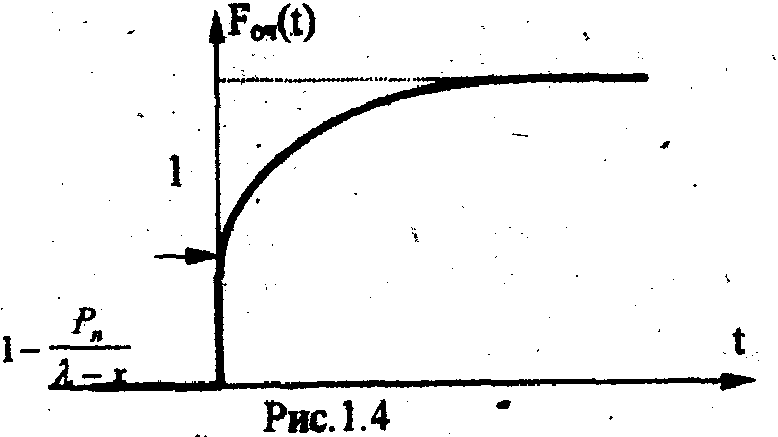

Довольно часто имеет место случай, когда есть всего один канал обслуживания (n=l). В этом случае все формулы значительно упрощаются: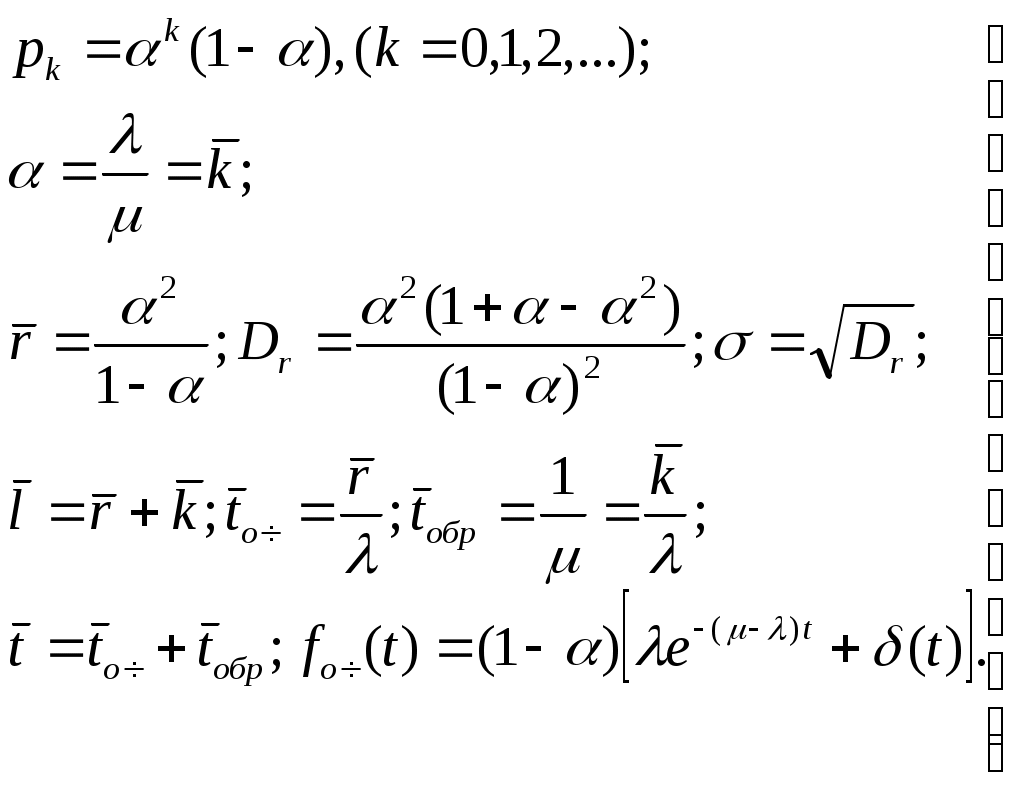

(1.19)
Время обработки документа Т_обр является случайной величиной, подчиненной показательному закону с параметром:

. (1.20)

Время нахождения в системе:

T=T_оч+T_обр.
2. Математическая модель процесса накопления информации

Рассмотрим процесс накопления информации. Ограничения на число состояний для этого процесса не накладываются. Это означает, что нет практических ограничений на число накапливаемых информационных документов в базах данных.

Интенсивность потока событий λ-интенсивность потока входных документов; интенсивность потока событий μ-ингенсивность изъятия документов из фондов, а состояние X_k состоит в том, что в момент времени t в фонде находится k информационных документов. Если интенсивность изъятия, одного документа μ есть величина постоянная, то это означает, что каждый принятый на хранение документ будет находиться в базах данных случайное время Т , распределенное по показательному закону с математическим ожиданием:

.
В соответствии с размеченным графом состояний система дифференциальных уравнений для вероятностей состояний будет иметь вид:

(2.1)

. (2.1)

где,

.

В выражении (2.1) интенсивности потоков событий λ и μ могут быть любыми неотрицательными функциями времени, но для сокращения записи зависимости интенсивностей потоков λ и μ στ времени t опущены.

Найдем математическое ожидание случайной функции X(t), для чего правые и левые части уравнения для производной

умножим на k и проведем суммирование по всем k:

. (2.2)

Проведем ряд несложных алгебраических вычислений и, считая, что математическое ожидание случайной функции X(t) существует, можно получить следующее выражение:

. (2.3)

. (2.4)

При постоянных

получим:

,

а при m_xo=0 это выражение примет такой вид:

(2.5)

Найдем второй начальный момент случайной функции X(t)

,

для чего правые и левые части уравнения (2.1) умножим на k² и сложим:

. (2.6)

Проделав ряд преобразований этого выражения, получим следующее дифференциальное уравнение для второго начального момента (если такой существует):

. (2.7)

Дисперсию случайной функции X(t) можно выразить через второй и первый начальные моменты:

. (2.8)

Продифференцируем левую и правую части равенства (2.8) и используем равенства (2.3) и (2.7). После несложных преобразований получим:

. (2.9)

Заметим еще раз, что уравнения (2.3) и (2.9) справедливы и в том случае, когда интенсивности потоков λ и μ являются любыми неотрицательными функциями времени.

В случае, если интенсивности потоков λ и μ являются постоянными, решение дифференциального уравнения (2.9) при начальных условиях

имеет вид:

. (2.10)

При достаточно большом математическом ожидании

закон распределения сечения случайной функции X(t) можно приближенно считать нормальным с характеристиками

.

Если максимальное число информационных документов в базах данных ограничено и равно n , то дифференциальное уравнение для математического ожидания и дисперсии числа накопленных документов будет иметь вид:

. (2.12)

Для рассмотренного выше случая, когда

, получим

; (2.13)

. (2.14)

При

и уравнение (2.3) и (2.14) будут совпадать с уравнениями (2.3) и (2.9).
3.Математическая модель режима работы информационного фонда с точки зрения пользователя
Обозначим величиной λ_n интенсивность обращения каждого из m внешних пользователей в банк данных с запросами.· На каждый запрос в среднем выдается k первичных информационных документов (ПИД). В этом случае интенсивность выдачи документов из фонда на запросы m внешних пользователей будет

.

Будем вначале рассматривать случаи, когда пользователю выдается копия ПИД поэтому любой пользователь всегда получает заказанный ПИД.

Обозначим среднее время задержки внешним пользователем ПИД при его получении величиной

(в это время можно включать и время копирования ПИД), тогда интенсивность возврата внешним пользователем каждого взятого по запросу ПИД будет равна γ.

В этом случае можно рассмотреть два взаимосвязанных процесса:

х(t) - число ПИД в фонде;

у(t) - число ПИД, находящихся у внешнего пользователя.

Схема взаимодействия таких процессов показана на рис.3.1.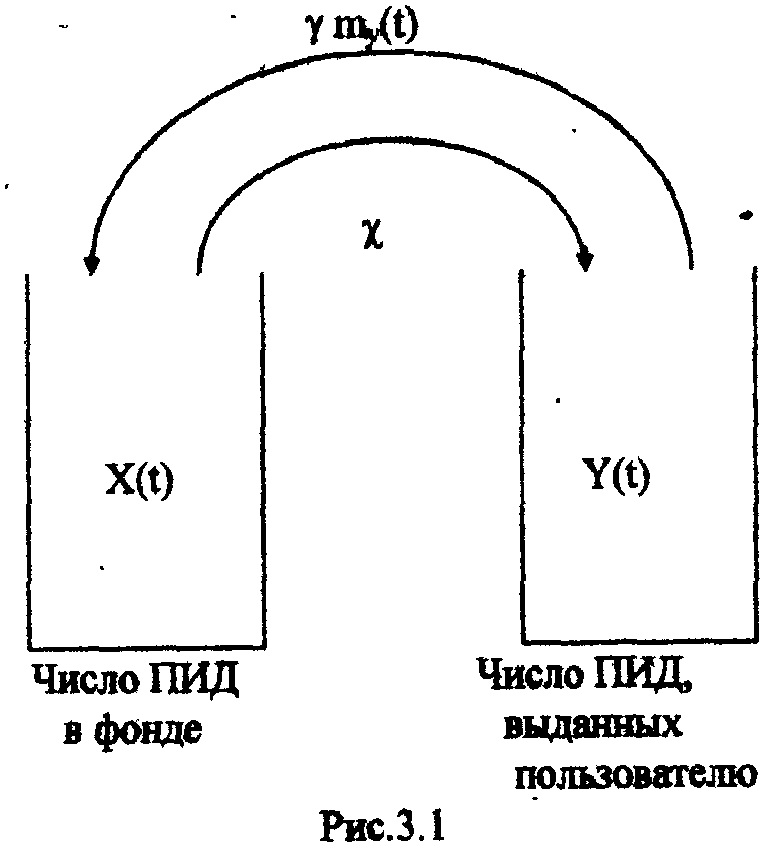

Суммарная интенсивность возвращения ПИД внешними пользователями в фонд будет равна

, где

- математическое ожидание числа ПИД находящихся у внешнего пользователя. .В соответствии со схемой можно составить дифференциальные уравнения для математического ожидания и дисперсии случайной функции у(t):

;

.

Заметим, что в нашем случае величины m_y(t) и D_y(t) не зависят от того, сколько имеется ПИД в фонде. Это объясняется тем, что каждый затребованный ПИД внешним пользователем выдается ему в виде копии.

При

=const,

=const и

можно найти стационарное решение:

/

Так например, если

m=lOO, К=3, λ_n=1[1/сутки],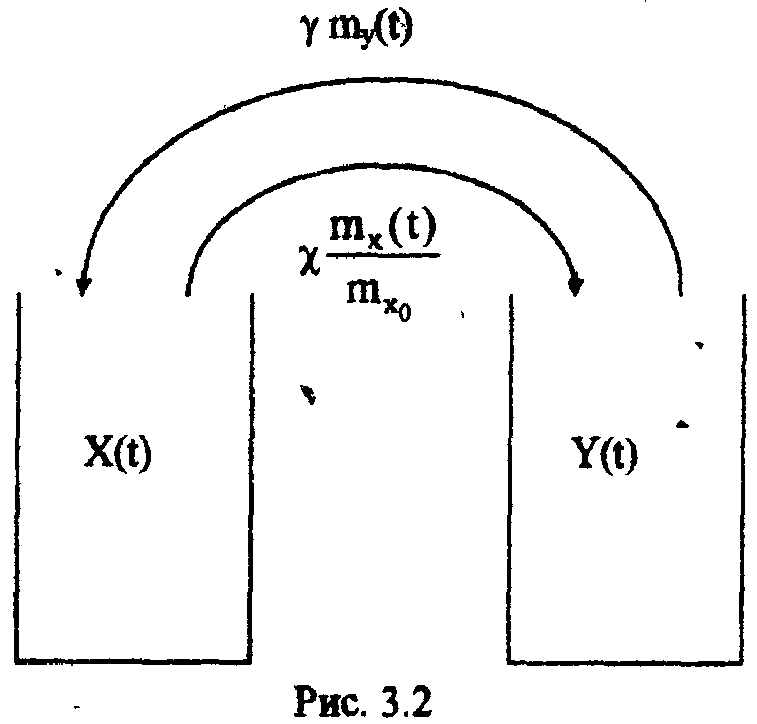

=1/10[1/сутки], m_y=D_y=3000 ПИД, т.е. в среднем у каждого пользователя будет 3000 ПИД. Рассмотрим теперь случай, когда пользователям выдаеться ПИД, который имеется в фонде в единственном экземпляре. В этом случае интенсивность выдачи ПИД из фонда будет не χ,,а

где

- приближенное значение вероятности наличия затребованного ПИД в фонде, а величина

общее количество ПИД в фонде (рис.3.2).

В этом случае система дифференциальных уравнений для величин m_х(t) и m_y(t) будет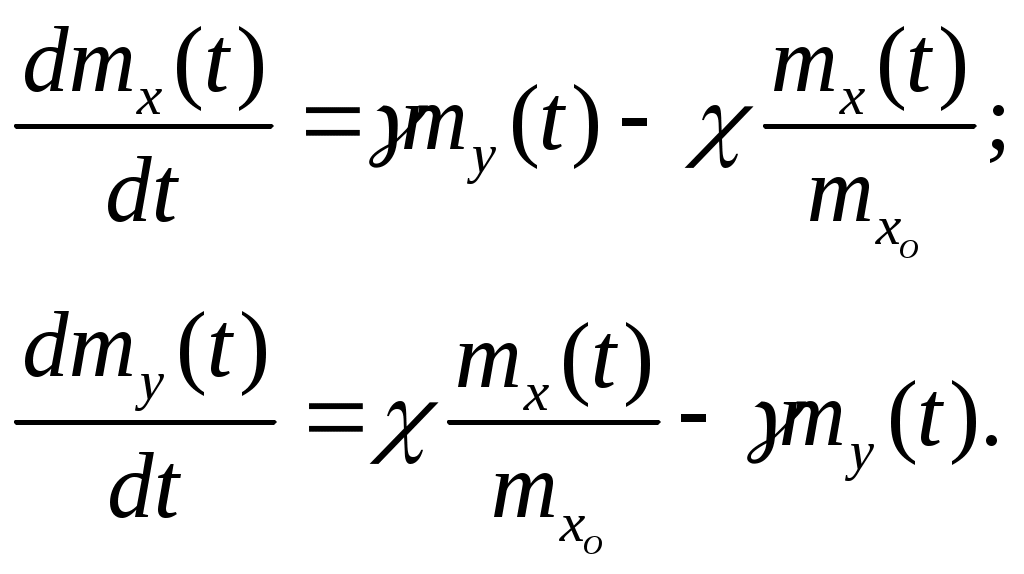

Найдем решение этой системы для стационарного режима, который существует при χ = const, m_xo=const,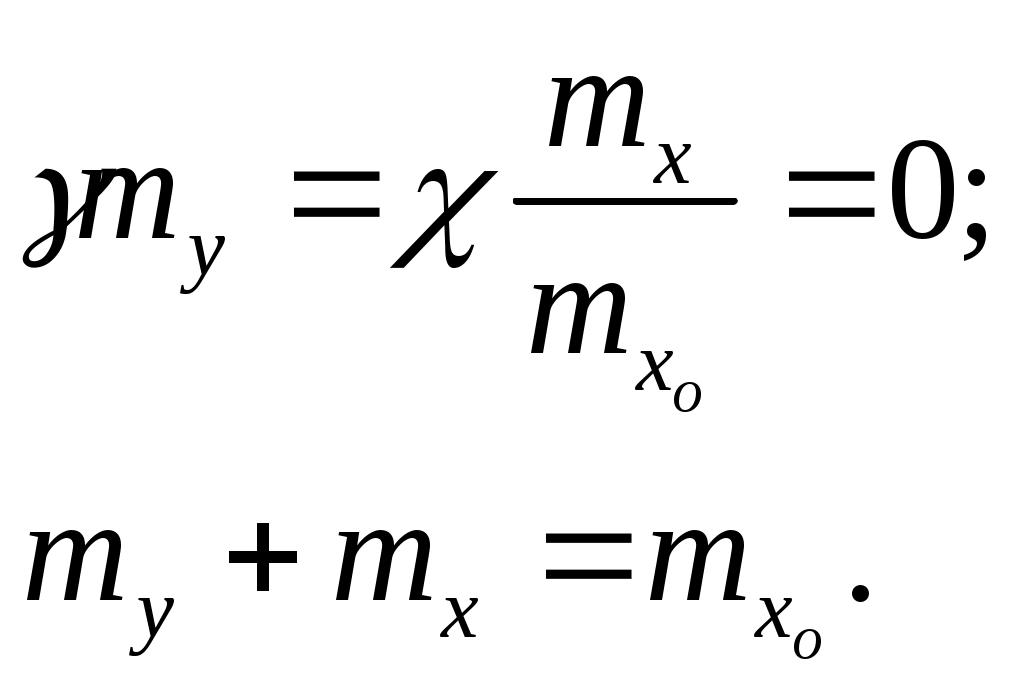

=const и t

Решая эту систему уравнений, получим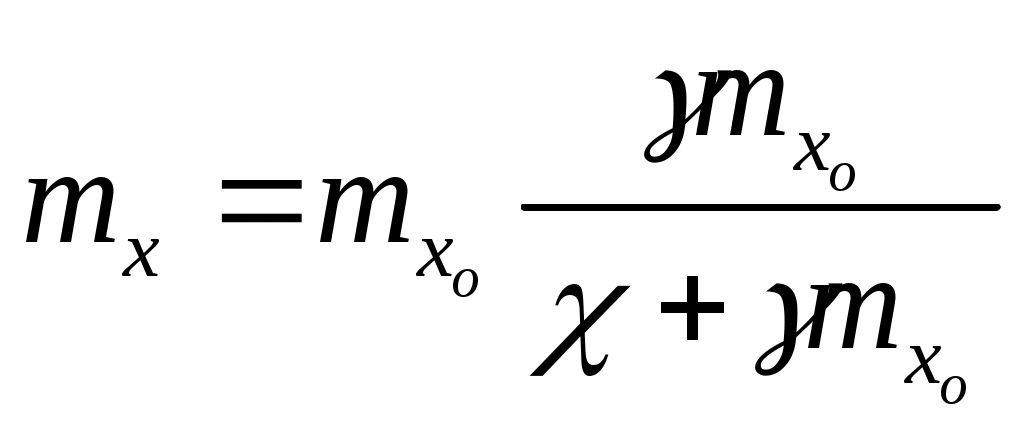

.

Среднее время ожидания возврата ПИД затребованного внешним пользователем в фонде, будет определятся по формуле

Если среднее время ожидания возврата ПИД является неприемлемым для внешних пользователей, то необходимо вводить копирование всех ПИД при их выдаче или иметь копии всех ПИД.
Подготовка к лабораторной работе

Лабораторная работа рассчитана на 4 часа (2 лабораторных занятия) работы в лаборатории и 2 часа самостоятельной подготовки, которая состоит из изучения кратких теоретических сведений, подготовки блок-схемы, программы на алгоритмическом языке для получения конечных результатов, предусмотренных в каждом конкретном случае.

Для допуска к лабораторной работе необходимо предъявить блок-схемы по своему варианту и ответить на вопросы по теоретической части лабораторной работы.

Содержание лабораторной работы

1 Составить по блок схеме программу на алгоритмическом языке для решения доставленной задачи.

2.Сдать программу на ВЦ для машинной реализации.

3.Лийтинги с результатами проанализировать, если не получен результат, то ошибки исправить и сдать новую реализацию.

4.Провести анализ полученных результатов и сделать вывод,

Содержание отчета

\

Отчет должен содержать:

1 .Задание на лабораторную работу в полном объеме.

2.Блок-схемы алгоритмов для конкретного варианта.

3.Лийстинги программы и результаты.

4.Выводы по полученным результатам.

Вопросы для самопроверки

1 .Параметры пуассоновского потока. Особенности стационарного режима работы.

2.Время переходного процесса системы обслуживания.

3.Особенности математической модели процесса накопления информации.

4.Особенности математической модели режима работы информационного фонда с точки зрения пользователя.

5.Среднее число документов в подсистеме обработки документов.

6.Среднее время нахождения документа в системе обработки информации.

7.Параметры, определяющие погребное количество персонала фонда.

8.Параметры, определяющие среднее число документов у каждого пользователя в режиме работы фонда с точки фения пользователя.

9.Интенсивность выдачи документов из фонда на запросы внешних пользователей.

Приложение

Индивидуальные задания 1.

1.Подсистема обработки информации.

1 2 3 4 5 6 7 8 9 10 11