Метод_указания к Лабораторным работам (1). Структурную и функциональную классификацию вс
 Скачать 2.03 Mb.
|
|
Описание блок-схемы алгоритма (рис.п.1.1 -п. 1.8) Данная программа предназначена для моделирования информационных подсистем. Моделируются подсистемы: обработки информации, накопления информации, работы системы с точки зрения пользователя. Программа реализована на языке Turbo Pascal 7.0. Описание входных данных LAM-интенсивность потока необработанных документов на входе системы обработки информации; MUO-интенснвность обработки документов в каждом канале; ΜUΙ-интенсивность изъятия документов из фонда; S-площадь фонда необходимая для хранения одного документа; NS-количество сотрудников, необходимое для подготовки и хранения одного документа; KD-интенсивность обращения каждого внешнего пользователя с запросом; М-число внешних пользователей; LP-среднее количество первичных информационных документов, выдаваемых на каждый запрос; GАМ-среднее время задержки внешним пользователем документа при его получении; МX-общеее количество документов в фонде. Блоки 3-35 модель подсистемы обработки информации Блок 4-8 - определяется число каналов обработки информации N необходимое для стационарного режима работы системы. Блок 10 - определяется среднее число занятых каналов обработки информации (среднее число обрабатываемых документов в данный момент времени). Блок 12-21 - вычисляется вероятность того, что в системе обработки информации имеется N информационных документов, все они обрабатываются и очереди из необработанных документов нет (ΡΝ). Блок 22 - среднее число необработанных документов, находящихся в очереди на обработку. Блоки 24, 26 - вычисляется дисперсия и среднее квадратическое отклонение числа документов в очереди D и G. Блок 28 - среднее число документов, находящихся в системе обработки информации L. 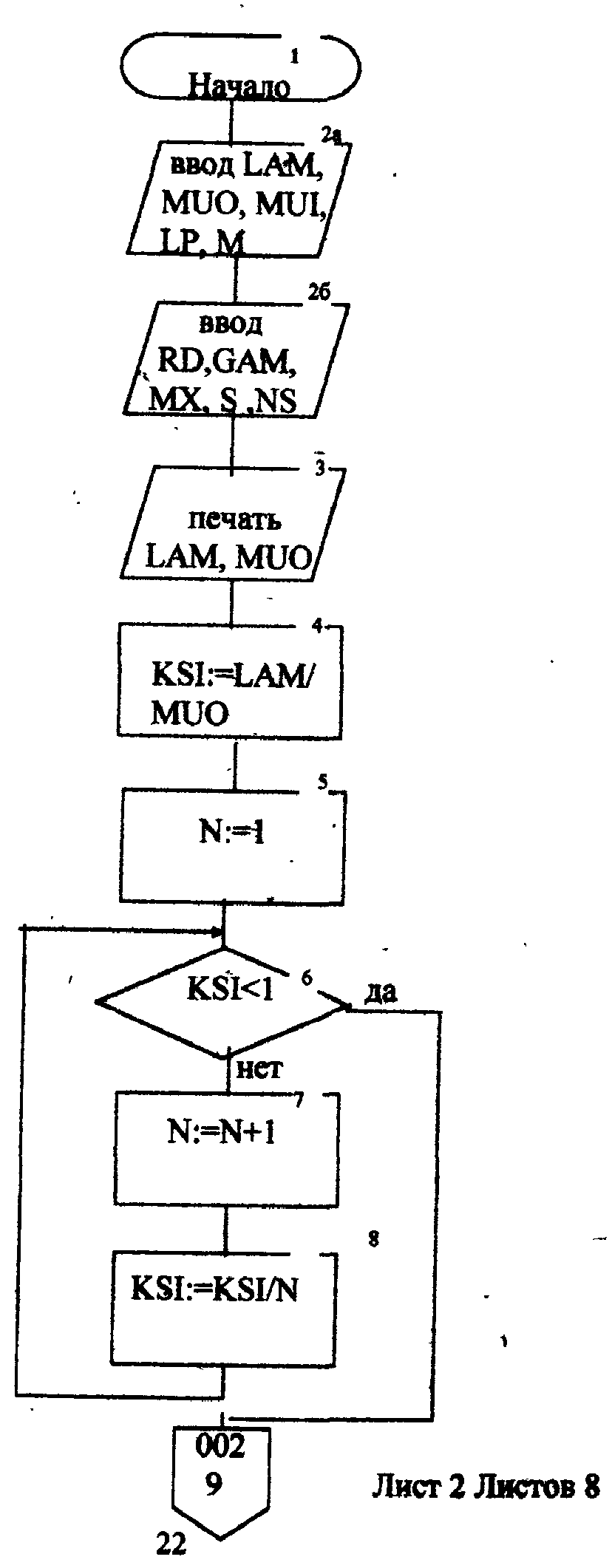 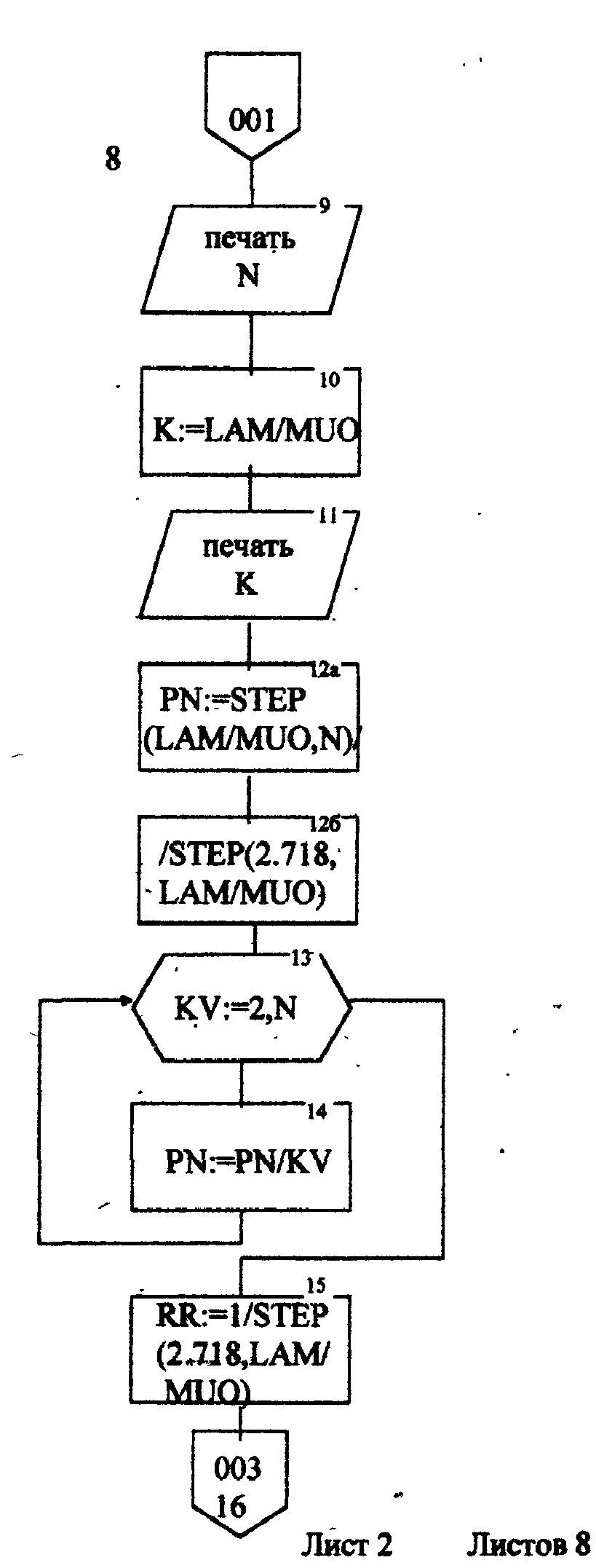 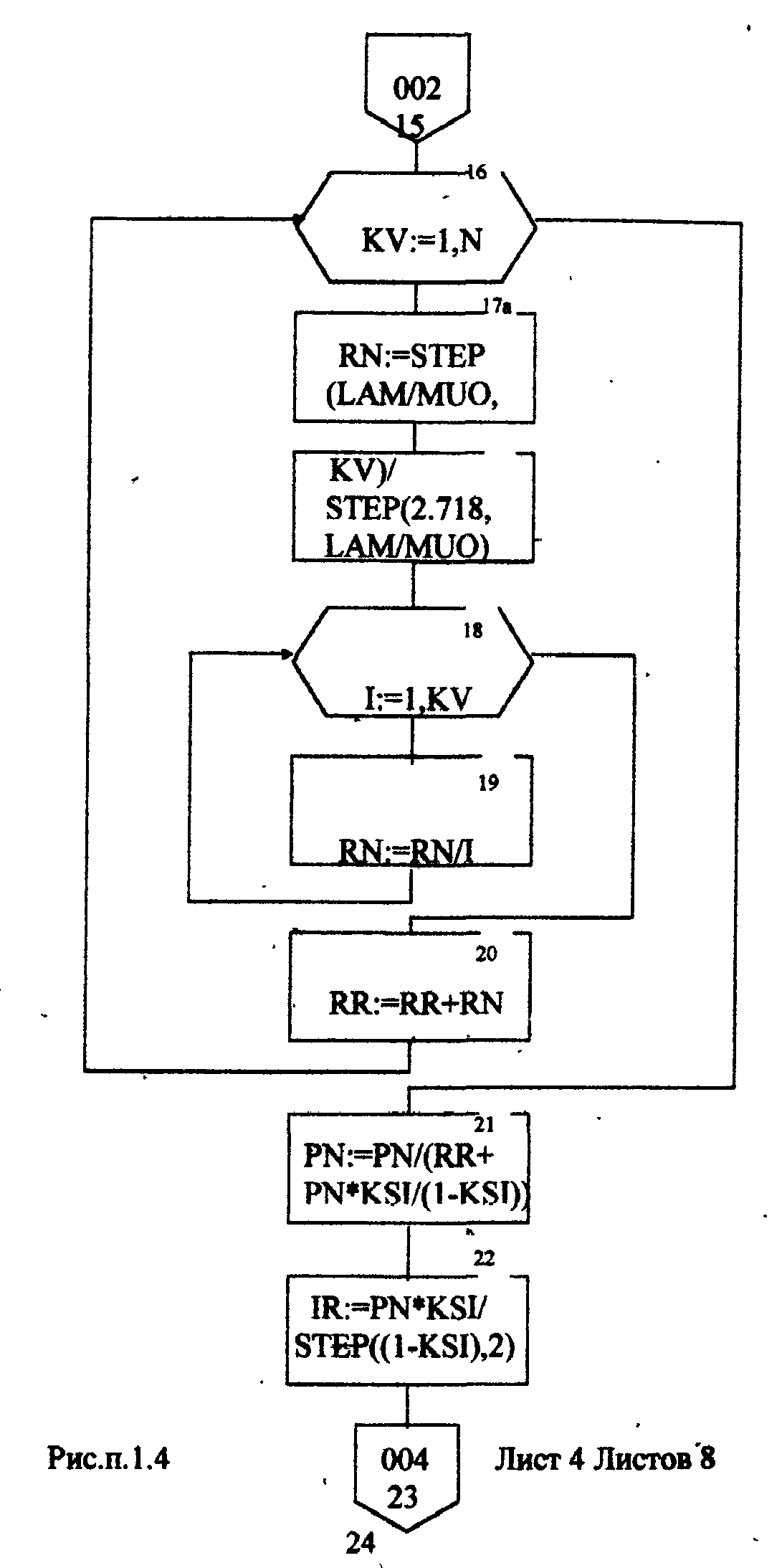 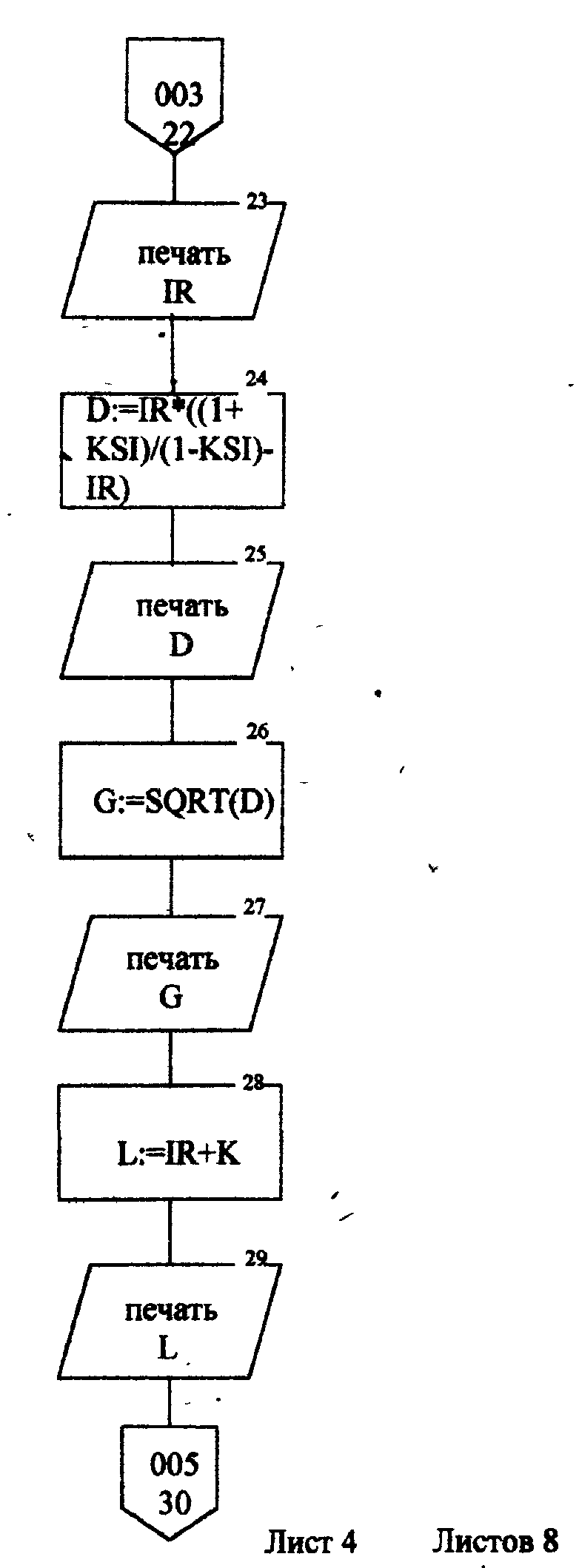 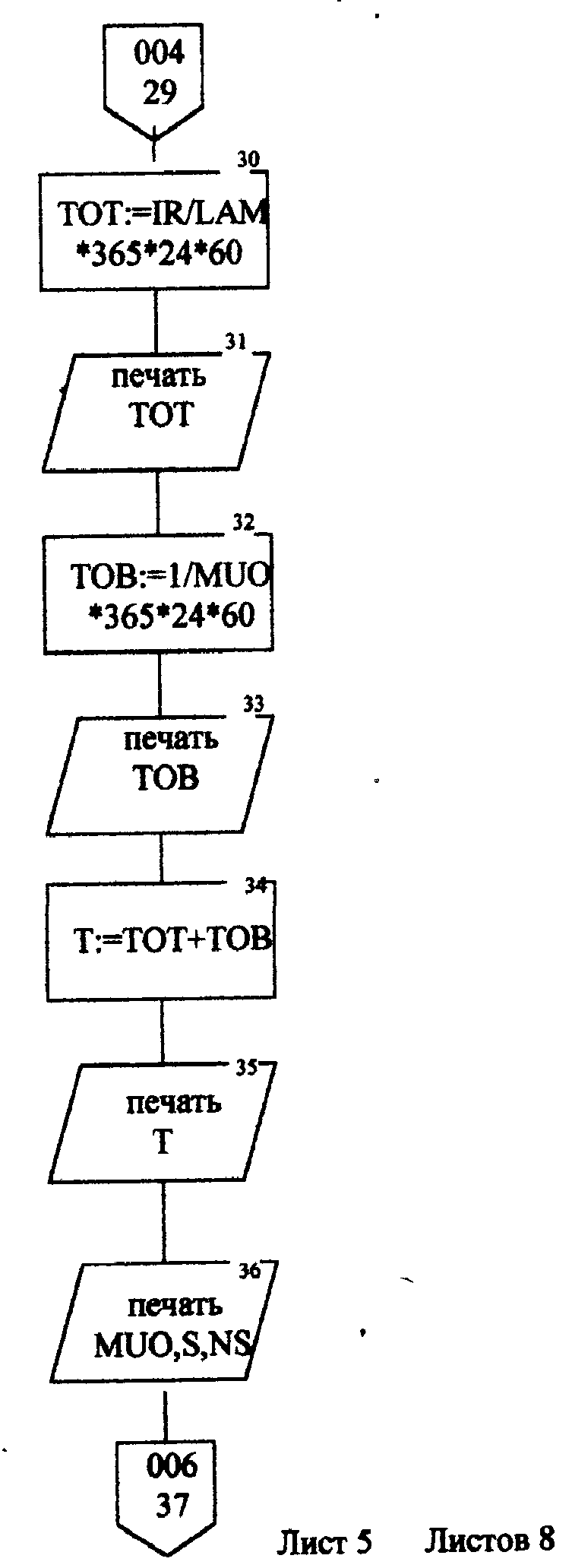 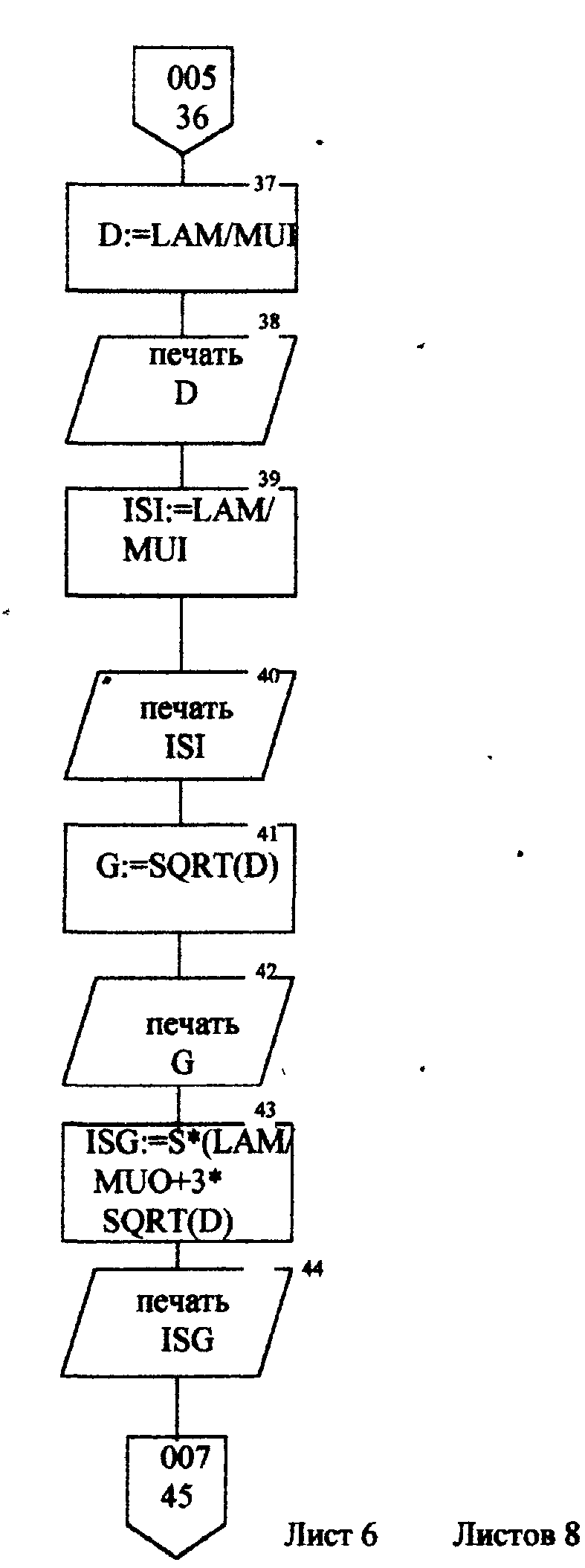 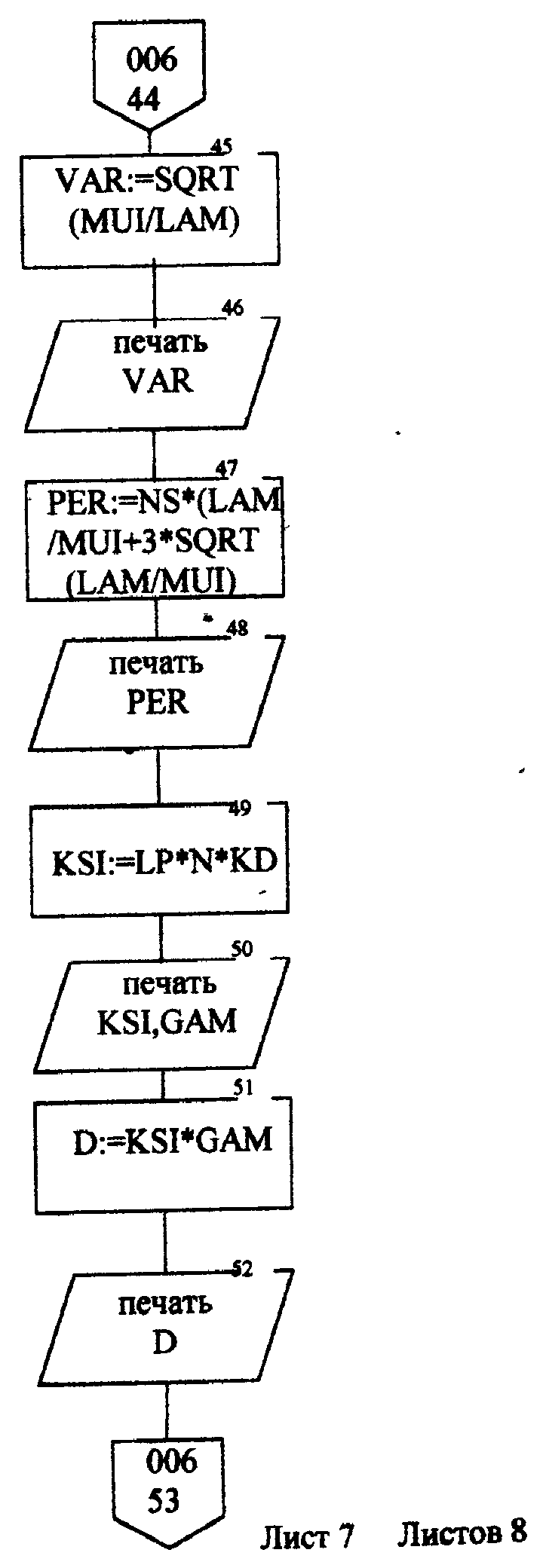 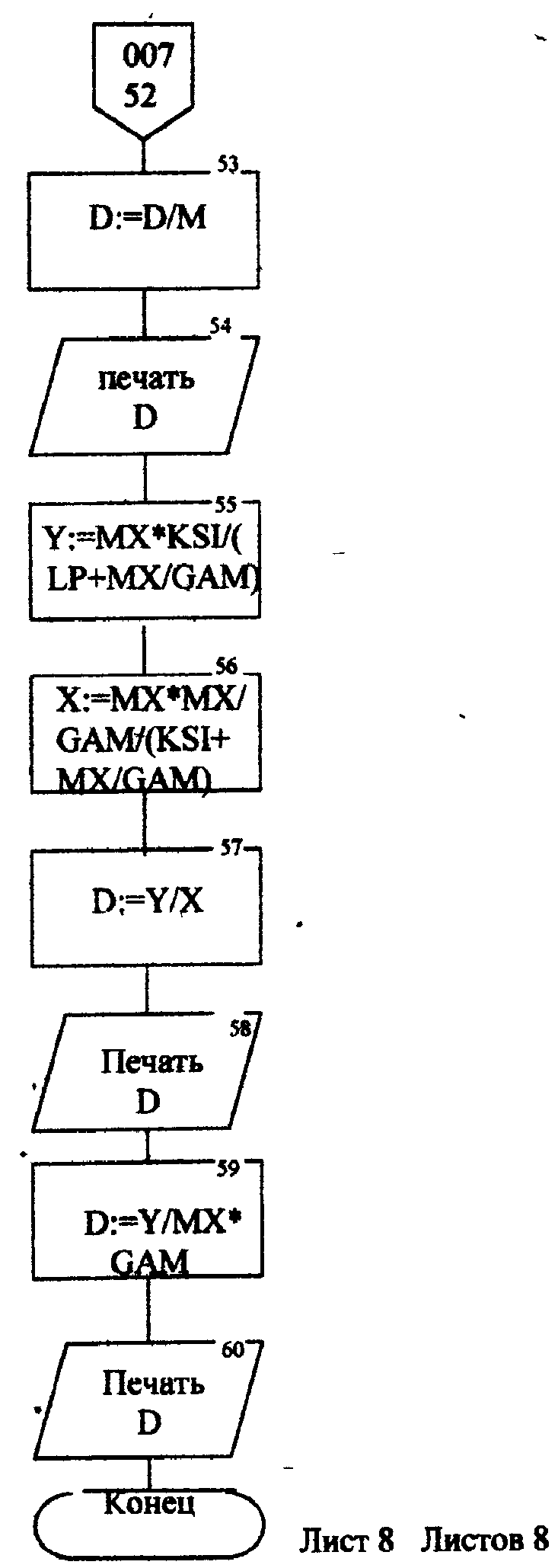 Блок 30 · определяется время нахождения документа в «очереди» на обработку ТОТ (в минутах). Блок 32 · определяется время нахождения документа на обработку ТОВ (в минутах). Блок 34 - среднее время нахождения документа в системе обработки информации Т (в минутах). Блоки 36 - 48 - подсистема накопления информации Блок 37 - вычисляется дисперсия D при стационарном режиме. Блок 39 - определяется число документов в фонде в установившемся режиме (IST). . Блок 41 - определяется среднее квадратическое отклонение числа хранимых в фонде документов. Блок 43 - определяется площадь фонда ISG, необходимая для хранения документов. Блок 45 - коэффициент вариации числа хранимых в фонде документов. Блок 47 -рассчитывается потребное количество персонала (PEP). Блоки 49 - 60 - режим работы фонда с точки зрения пользователя. Блок 49 - интенсивность выдачи документов из фонда на запросы Μ внешних пользователей (KSI). Блок 51 - определяется дисперсия D при стационарном режиме. Блок 55 - определяется среднее количество документов, находящихся у каждого пользователя. Блок 57 - определяется вероятность того, что внешний пользователь, обратившийся в фонд за документом, не застанет его в фонде. Блок 59 - определяется среднее время ожидания возврата документа, затребованного внешним пользователем. Блок 61 - конец. Листинг программы на языке Turbo Pascal 7.0. program Model; uses crt; var mx,lam,muo,lp,m,kd,gam,n,kv,i: longint; ns,s,mui,ksi,k,pn,rr,rn,ir,d,g,l,tot,tob,t,ist,isg,Var1,per,x,y: real; ch:char; function step(a,b:real):real; var x: real; begin x:=exp(ln(a)*b); step:=x; end; begin clrscr; writeln('Интенсивность потока необработанных документов на входе'); write('системы обработки информации LAM ='); readln(lam); writeln('Интенсивность обработки документов в каждом канале MUO ='); readln(muo); writeln('Интенсивность изъятия документов из фонда MUI = '); readln(mui); write('Интенсивность обращения каждого внешнего пользователя с запросом LP ='); readln(lp); write('Число внешних пользователей М ='); readln(m); writeln('Среднее время задержки внешним пользователем документа при'); write('его получении GAM = '); readln(gam); write('06щее количество документов в фонде MX = '); readln(mx); write('Площадь фонда, необходимая для хранения одного документа S='); readln(s); writeln('Количество сотрудников, необходимое для подготовки и хранения'); write('одного документа NS ='); readln(ns); writeln('Haжмите любую клавишу...'); repeat until keypressed; ch:=readkey; if ch=#0 then ch:=readkey; clrscr; writeln('LAM=',lam,'MUO=',muo); ksi:=lam/muo; n:=1; while ksi>=l do begin n:=n+1; ksi:=ksi/n; end; writeln('Число каналов обработки информации, необходимое для стационарного'); write('режима работы='); writeln(n); readln; k:=lam/muo; write('Cpeднee число занятых каналов обработки информации='); writeln(k:10:4); readln; pn:=step(lam/muo,n)/step(2.718,lam/muo); for kv:=2 to n do pn:=pn/kv; rr:=1/step(2.718,lam/muo); for kv:=1 to n do begin rn:=step(lam/muo,kv)/step(2.718,lam/muo); for i:=1 to kv do rn:=rn/i; rr:=rr+rn; end; pn:=pn/(rr+pn*ksi/(1-ksi)); ir:=pn*ksi/step(1-ksi,2); writeln('Cpeднee число необработанных документов, находящихся в'); write('"очереди" на обработку"'); writeln(ir:10:4); readln; d:=ir*(-ir+(1+ksi)/(1-Ksi)); write('Дисперсия числа документов в очереди='); writeln(d:10:4); readln; g:=sqrt(d); write('Среднee квадратическое отклонение числа документов в очереди='); writeln(g:10:4); readln; l:=ir+k; write('Cpeднee число документов, находящихся в системе обработки информации='); writeln(l:10:4); readln; tot:=ir/lam*365*24*60; write('Cpewee время нахождения документа в очереди на обработку='); writeln(tot:10:4); readln; tob:=l/muo*365*24*60; write('Среднее время нахождения документа на обработке='); writeln(tob:10:4); readln; t:=tot+tob; write('Cpeднee время нахождения документа в системе обработки информации='); writeln(t:10:4); readln; writeln('MUI=',mui:10:4,' S=',s:10:4,' NS=',ns); d:=lam/mui; write('Дисперсия при стационарном режиме='); writeln(d:10:4); readln; ist:=lam/mui; write('Числo документов в фонде в установившемся режиме='); writeln(ist:10:4); readln; g:=sqrt(d); writeln('Cpeднee квадратическое отклонение числа хранимых в фонде'); write('документов='); writeln(g:10:4); readln; isg:=s*(lam/mui+3*sqrt(d)); write('Площадь фонда, необходимая для хранения документов='); writeln(isg:10:4); readln; var1:=sqrt(mui/lam); write('Коэффициент вариации числа хранимых в фонде документов ='); writeln(var1:10:4); readln; per:=ns*(lam/mui+3*sqrt(lam/mui)); write('Пoтpe6нoe число персонала='); writeln(per:10:4); readln; ksi:=lp+n*kd; writeln('Интенсивность выдачи документов из фонда на запросы внешних'); write('пользователей='); writeln(ksi:10:4); readln; writeln('GAM=',gam); d:=ksi*gam; write('Дисперсия в стационарном режиме='); writeln(d:10:4); readln; d:=d/m; writeln('Дисперсия в стационарном режиме='); writeln(d:10:4); readln; x:=mx*ksi/(lp+mx/gam); y:=(mx/(ksi+mx/gam))*(mx/gam); d:=y/x; writeln('Bepoятность того, что внешний пользователь, обратившийся в фонд за'); write('документом, не застанет его в фовде='); writeln(d:10:4); readln; d:=y/mx*gam; writeln('Cpеднее время ожидания возврата документа, затребованного внешним'); write('пользователем='); writeln(d:10:4); readln; writeln('Нажмите любую клавишу...'); repeat until keypressed; ch:=readkey; if ch=#0 then ch:=readkey; end. Лабораторная работа №3 Тема: «Экспериментальное определение количества информации, избыточности источника сообщений» Цель работы: Экспериментальное определение количества информации, избыточности источника сообщений. 1. Основные понятия Важнейшим вопросом теории информации является установление меры количества и качества информации. Существует несколько методов оценки количества информации: структурные методы, статистические и семантические. В данной лабораторной работе будут рассматриваться статистическая мера количества информации и структурная мера. К структурным мерам информации относится широко распространенная аддитивная мера Хартли, которая предполагает измерение информации в двоичных единицах – битах. Количество информации по Хартли определяется следующим образом:  (бит), (1.1)где I - количество информации; Q – число; L- длина числа (количество разрядов); h - глубина числа (алфавит основание). В этом случае, при L =1 и h =2, получаем L =1 бит. При вероятностном подходе информация рассматривается как сообщение об исходе случайных величин и функций, а количество информации ставиться в зависимость от априорных вероятностей этих величин, событий, функций. Для количественного определения информации можно использовать любую монотонно убывающую функцию вероятностей F [P(a)] Примером простейшей функции такого класса является функция вида  ,где Р(а)- вероятность появления сообщения а. Неопределенность каждой ситуации характеризуется величиной, называемой энтропией. В статической теории информации предложенной Шенноном, энтропия количественно выражается как средняя функция множества вероятностей каждого из возможных исходов опыта. Таким образом, энтропия по Шеннону определяется следующим образом (1.2):  , (бит) (1.2)где Pi- вероятности отдельных исходов; К - число разных исходов опытов из N возможных. Основание логарифма определяет единицу измерения энтропии и количества информации (бит). Энтропия характеризуется следующими свойствами: 1. Энтропия всегда положительна 2. Энтропия равна нулю в том случае, когда вероятность появления одного события равна 1, а все остальные -О. 3. Энтропия имеет наибольшее значение в том случае, когда все вероятности равны между собой: Ρ1=Ρ2=Ρκ=  , в этом случае  , (1.3)Если некоторый источник сообщения содержит N символов, тогда количество информации можно определить по формуле (1.4):  , (1.4)а избыточность источника сообщений:  ,где Η- энтропия на один символ данного источника; Нmax-максимальная энтропия. При Н=Нmax R=0;приН=0 R=l. Следовательно,  .Чем меньше избыточности R, тем больше информационной нагрузки приходится на каждый вырабатываемый символ, тем рациональнее работает источник. 2.Определение количества информации. Восприятие человека зависит от его состояния, т.е. от загруженности, утомляемости и т.д. При наличии данных факторов и их возрастании возбуждаемость нервной системы падает и, следовательно, снижается уровень восприятия. В общем случае процесс восприятия информации будет аналогичен процессу передачи сообщения по каналу с шумами. В канале с шумами по принятому сигналу только с некоторой вероятностью P(a/v) Тогда количество информации, содержащееся в сигнале, определяется степенью уменьшения неопределенности при его приеме. Если Р(а) - априорная вероятность, то количество информации в принятом сигнале V относительно переданного сообщения, а будет равно (2.1)  . (2.1)Выражение (2.1) можно рассматривать, кроме того, как разность между количеством информации, поступившим от источника сообщений и тем количеством информации, которое потеряно в канале за счет действия шумов. При подсчете количества информации возможны два пути: 1) Подсчет количества информации, содержащейся в тексте, составленном из букв русского алфавита, параллельно с подсчетом количества информации, содержащейся в формулах (латинский алфавит); 2) Представление формул в символах русского алфавита. Второй путь более рационален, т.к. первый не позволяет сравнивать технические и общественные науки по информативности. Для подсчета информативности текста необходимо иметь таблицу вероятностей появления той или иной буквы русского . алфавита (см. табл. 1). При подсчете количества информации .приходящегося на каждый из 32 символов , следует пользоваться формулой:  , (2.2)где m- число символов одного вида. Из таблицы 1 видно, что использовано 32 буквы русского алфавита, следовательно, в формуле (1.2) к=32. По заданию преподавателя требуется подсчитать количество информации, содержащейся в том или ином разделе текста. 3.Опредение информационной избыточности источника сообщений. Как уже отмечалось, избыточность источника сообщений определяется по формуле (1.5). Если энтропию Η измерять в битах и считать, что число символов k=32, тогда  или  .(3.1)Следовательно, основной задачей становиться вычисление энтропии Н. Ниже будет показано, как нужно решать эту задачу. Источник информации называется эргодическим, если корреляционные связи между символами последовательности, которую он генерирует, распространяются на конечное число N символов. Энтропия Н на символ такого источника в битах может быть вычислена по формуле:  , (3.2)где Р(bij) - вероятность появления последовательности символов в порядке i,j.  - условная вероятностьПрименительно к тексту, как к источнику информации, соотношение (3.2) можно интерпретировать как формулу для вычисления энтропии последующей буквы, когда известны предыдущие N-1 букв. При возрастании N в величине НN учитываются всё более и более далекие статистические связи между буквами, и энтропия НN является предельным значением НN при N   . (3.3)Значения НN для малых N могут быть вычислены непосредственно, если известны частоты или вероятности появления отдельных букв (Xj), двухбуквенных, трехбуквенных и т.д. сочетаний. Так, например, используя таблицу 1, получим:  , (3.4)где P(i) - вероятность появления соответствующей буквы. К сожалению, не так легко может быть вычислена энтропия при N=2,3,4 и т.д. Здесь возникают большие сложности. Во-первых, не существуют таблиц вероятностей двухбуквенных, трехбуквенных и т.д. сочетаний. В принципе такие таблицы можно попытаться составить экспериментально, для этого необходимо перечислить все  возможные буквенные сочетания из 32 различных букв, затем подсчитать для какого-либо достаточно длинного стандартного текста (200-300 страниц)·частоты появления этих сочетаний и принять эти частоты в качестве оценок для вероятностей появления.Однако, практически эта работа очень трудоемка. В самом деле количество сочетаний из 32 букв M=32m. Приведем лишь несколько начальных значений величины М:
|