Метод_указания к Лабораторным работам (1). Структурную и функциональную классификацию вс
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
|
Таким образом уже для m>3 составление таблицы становиться практически невыполнимой задачей. В данной работе для оценки величины Η применяется метод Шеннона (1.2). Этот метод предполагает использование - того факта, что каждый говорящий на данном языке обладает огромными трудно учитываемыми сведениями о статистике языка. Знакомство со словами, идиомами, стандартными оборотами и грамматикой позволяет, например, выправить неправильные или пополнять пропущенные при чтении символы или дополнить неоконченную фразу в разговоре. Экспериментальная демонстрация степени возможности предсказания русского текста может быть следующей: выберем короткий отрывок текста, неизвестный отгадывающему, и предложим последнему отгадывать текст по буквам. Если догадка оказалась правильной, то об этом сообщается отгадывающему и предлагается определить вторую букву. Если первая буква не отгадана правильно, то отгадывающему предоставляется вторая попытка и т.д. до тех пор, пока он не отгадает правильно. Типичный результат такого эксперимента показан ниже. В строках (1) выписан исходный текст, цифры в строках (2) указывают, сколько отгадываний потребовалось на данную букву.
Если бы отгадывающий назвал все 32 буквы с равной вероятностью, то на отгадывание данного текста из 32 букв потребовалось бы в среднем 512 попыток (на каждую букву в среднем 16 попыток). Однако, благодаря знанию языка, т.е. учету статистических связей между буквами и разной вероятностей букв, отгадывающий затратил всего 107 попыток или в среднем 3,34 попытки на букву. Необходимо отметить, что строка (2), которую, следуя Шеннону, назовем приведенным текстом, содержит столько же информации, что и строка (1), в том смысле, что возможно, в принципе, определить строку (1) по строке (2). Для этого отгадывающему необходим двойник, математически идентичный с оригиналом. Если имеется только приведенный текст (2), тогда двойнику·предлагается последовательно отгадывать буквы текста столько раз, сколько единиц соответствует числу в приведенном тексте, таким образом восстанавливается исходный текст (1). Следовательно, приведенный текст можно рассматривать как закодированный вариант исходного. Для иллюстрации зависимости качества предсказания текста от числа N предшествующих букв, известных отгадывающему, можно поставить следующий эксперимент. Отгадывающему предлагается отгадать 10 произвольных предложений по 15 букв. Результаты подобного эксперимента дают таблицу, аналогичную таблице 2. Столбец N соответствует числу известных предшествующих букв, номер строки S указывает число попыток отгадывания. На пересечении N-го столбца и S-й строки стоит число раз, при которых опознавание правильной буквы произошло при 1-й попытке, когда известны предыдущие N-1 букв. Например, число 2 на пересечении 15-го столбца и 2-ой строки означает, что при известных 14 предшествующих буквах правильная буква была получена в 2-х случаях из 10 при второй попытке. Если ни одна из предшествующих букв не задана, то наиболее вероятным символом является пробел между словами (вероятность 0,145). В случае если первая попытка кончилась неудачей, следующей должна быть буква «о» (вероятность 0,095) и т.д. Эти вероятности есть частоты символов 1,2,…,32 приведенного текста при условии, что ни один из предшествующих символов не известен (см. таблицу 1). Обозначим через giN частоту угадываний буквы на i-той попытке при известных N-1 предыдущих буквах. Очевидно, что giN есть не что иное, как частота символа N приведенного текста при условии, что известны N-1 предыдущих символов. Можно представить приведенный текст, в котором символы 1,2…,32 встречаются с частотами giN. Возможная максимальная энтропия на символ в таком языке равна: С другой стороны, энтропия приведенного текста, при условии, что N-1 предыдущих символов известны, совпадает с энтропией Η оригинального текста. Отсюда следует соотношение для оценки сверху NH Соотношение (3.6) используется в данной работе для оценки энтропии HN текста, поскольку при достаточно больших имеет место равенство Содержание лабораторной работы. 1. Каждый студент получает от преподавателя по 5 предложений русского текста длиной не менее 15 букв (включая пробелы), причем эти предложения должны быть известны только тому, кто их получает. 2. Затем происходит поочередное отгадывание текста (при этом необходимо использовать данные таблицы 1) Составляется список предложений оригинального (1) и приведенного (2) текста. 3. Составляется таблица, аналогичная таблице 2, где в клетку {NS}, заносится общее количество 4. По составленной таблице 2 вычисляются величины 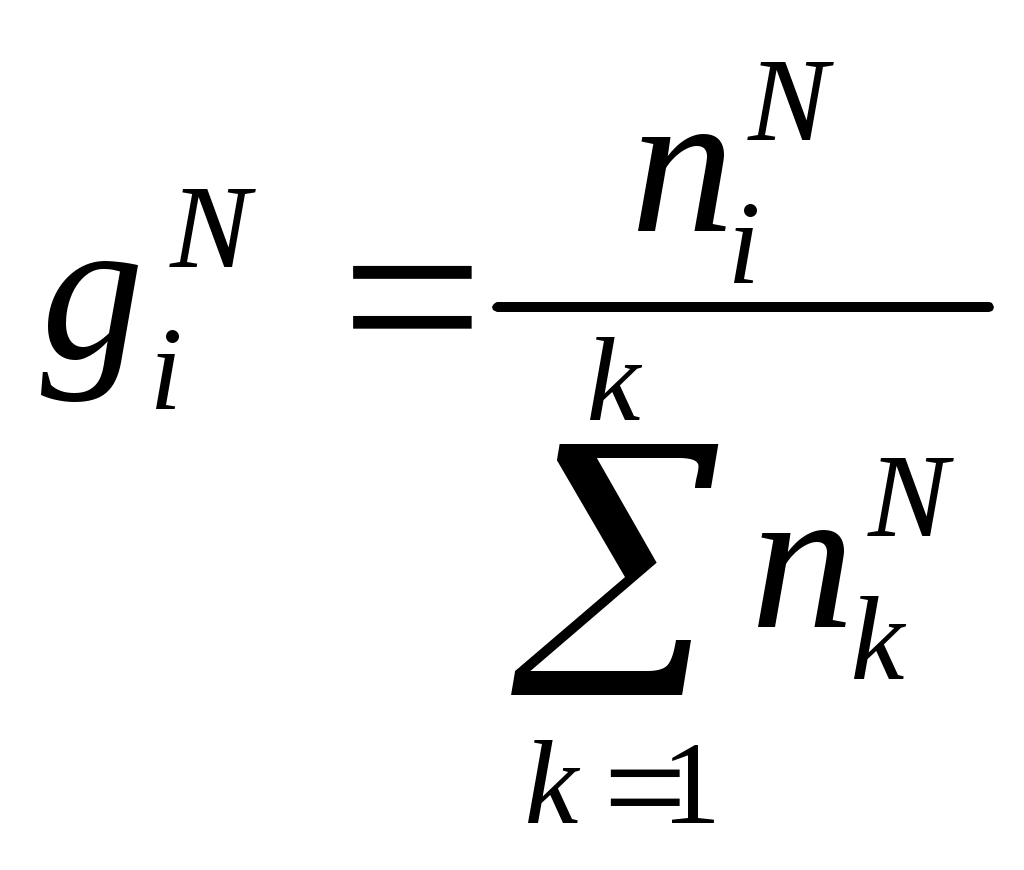 . .При вычислениях можно пользоваться таблицей 3. 5. Для каждого N вычисляется избыточность По полученным данным строится график RN(N). 6 Обработка результатов проводится на компьютере. Содержание отчёта. Отчет должен содержать 1 Исходный текст, предложенный преподавателем. 2 Результаты экспериментального определения количества информации (таблица 2). 3 График RN(N). Контрольные вопросы. 1. Перечислите основные методы оценки количества информации. 2. Расскажите об основных свойствах энтропии. 3. Почему трудно учесть вероятности для определения количества информации 2-х, 3-х и т.д. буквенных сочетаний? Таблица 1 Таблица вероятностей.
Таблица 2 Определение количества информации
|
