Гос экзамен по специальности Приборостроение. Ответы на вопросы ГОС экзамена. Тактильные датчики применяют для обнаружения объекта, установления момента
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
|
legend(stringl, string2,…, strings) — добавляет к текущему графику легенду в виде строк, указанных в списке параметров; >> legend('график') legend (Pos) — помещает легенду в точно определенное место, специфицированное параметром Pos: Pos=0 — лучшее место, выбираемое автоматически; Pos=l — верхний правый угол; Pos=2 — верхний левый угол; Pos=3 — нижний левый угол; Pos=4 — нижний правый угол; Pos=-l — справа от графика. При добавлении легенды следует учесть, что порядок и количество аргументов команды legend должны соответствовать порядку вывода графиков и их количеству Обычно графики выводятся в режиме автоматического масштабирования. Следующие команды класса axis меняют эту ситуацию: – axis([XMIN XMAX YMIN YMAX]) — установка диапазонов координат по осям х и у для текущего двумерного графика; – axis([XMIN XMAX YMIN YMAX ZMIN ZMAX]) – установка диапазонов координат по осям х, у и z текущего трехмерного графика; – axis auto — установка параметров осей по умолчанию; В математической, физической и иной литературе при построении графиков в дополнение к разметке осей часто используют масштабную сетку. Команды grid позволяют задавать построение сетки или отменять это построение: – grid on — добавляет сетку к текущему графику; – grid off — отключает сетку. Во многих случаях желательно построение многих наложенных друг на друга графиков в одном и том же окне. Для этого служит команда продолжения графических построений hold. Она используется в следующих формах: – hold on — обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже существующим; – hold off — отменяет режим продолжения графических построений; Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков: – subplot(m, n, p)— разбивает графическое окно на m×n подокон, при этом m — число подокон по горизонтали, n— число подокон по вертикали, а р — номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам). Проиллюстрируем работу функции subplot (см рис. 4.4): >>subplot(3, 2, 1); plot (x,y); >> subplot(3, 2, 4); plot (x,y); >> subplot(3, 2, 5); plot (x,y); Предназначение специальных символв в MATLAB: Квадратные скобки, пробел, запятая, точка с запятой, двоеточие, круглые скобки, точка, три точки и более, знак процента, апостроф Специальные символы
Блоки разделов библиотеки Simulink: Continuous, Discrete, Discontinuities, Signals Attribute Библиотека Simulink содержит следующие основные разделы: Continuous – линейные блоки. Discrete – дискретные блоки. Functions & Tables – функции и таблицы. Math – блоки математических операций. Nonlinear – нелинейные блоки. Signals & Systems – сигналы и системы. Sinks - регистрирующие устройства. Sources — источники сигналов и воздействий. Subsystems – блоки подсистем 9.3. Continuous – аналоговые блоки 9.3.1. Блок вычисления производной Derivative Назначение: Выполняет численное дифференцирование входного сигнала. Параметры: Нет. Для вычисления производной используется приближенная формула Эйлера: где Значение входного сигнала блока до начала расчета считается равным нулю. Начальное значение выходного сигнала также полагается равным нулю. Точность вычисления производной существенно зависит от величины установленного шага расчета. Выбор меньшего шага расчета улучшает точность вычисления производной. На рис. 9.3.1 показан пример использования дифференцирующего блока для вычисления производной прямоугольного сигнала. В рассматриваемом примере, для повышения наглядности, шаг расчета выбран достаточно большим. 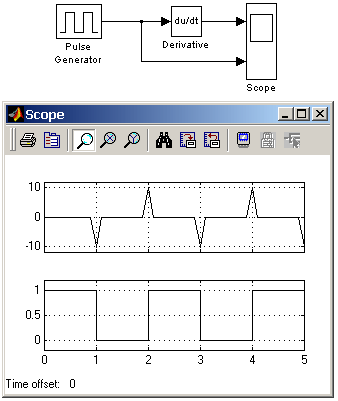 Рис.9.3.1. Использование блока Derivative для дифференцирования сигнала. [Скачать пример] Данный блок используется для дифференцирования аналоговых сигналов. При дифференцировании дискретного сигнала с помощью блока Derivative его выходной сигнал будет представлять собой последовательность импульсов соответствующих моментам времени скачкообразного изменения дискретного сигнала. 9.3.2. Интегрирующий блок lntegrator Назначение: Выполняет интегрирование входного сигнала. Параметры: External reset – Внешний сброс. Тип внешнего управляющего сигнала, обеспечивающего сброс интегратора к начальному состоянию. Выбирается из списка: none – нет (сброс не выполняется), rising - нарастающий сигнал (передний фронт сигнала), falling - спадающий сигнал (задний фронт сигнала), either – нарастающий либо спадающий сигнал, level – не нулевой сигнал (сброс выполняется если сигнал на управляющем входе становится не равным нулю); В том случае, если выбран какой-либо (но не none), тип управляющего сигнала, то на изображении блока появляется дополнительный управляющий вход. Рядом с дополнительным входом будет показано условное обозначение управляющего сигнала. Initial condition source — Источник начального значения выходного сигнала. Выбирается из списка: internal – внутренний external – внешний. В этом случае на изображении блока появляется дополнительный вход, обозначенный x0, на который необходимо подать сигнал задающий начальное значение выходного сигнала интегратора. Initial condition — Начальное условие. Установка начального значения выходного сигнала интегратора. Параметр доступен, если выбран внутренний источник начального значения выходного сигнала. Limit output (флажок) — Использование ограничения выходного сигнала. Upper saturation limit — Верхний уровень ограничения выходного сигнала. Может быть задан как числом, так и символьной последовательностью inf, то есть + Lower saturation limit — Нижний уровень ограничения выходного сигнала. Может быть задан как числом, так и символьной последовательностью inf, то есть - Show saturation port — управляет отображением порта, выводящего сигнал, свидетельствующий о выходе интегратора на ограничение. Выходной сигнал данного порта может принимать следующие значения: Ноль, если интегратор не находится на ограничении. +1, если выходной сигнал интегратора достиг верхнего ограничивающего предела. -1, если выходной сигнал интегратора достиг нижнего ограничивающего предела. Show state port (флажок) — Отобразить/скрыть порт состояния блока. Данный порт используется в том случае, если выходной сигнал интегратора требуется подать в качестве сигнала обратной связи этого же интегратора. На пример, при установке начальных условий через внешний порт или при сбросе интегратора через порт сброса. Выходной сигнал с этого порта может использоваться также для организации взаимодействия с управляемой подсистемой. Absolute tolerance — Абсолютная погрешность. На рис. 9.3.2 показан пример работы интегратора при подаче на его вход ступенчатого сигнала. Начальное условие принято равным нулю. 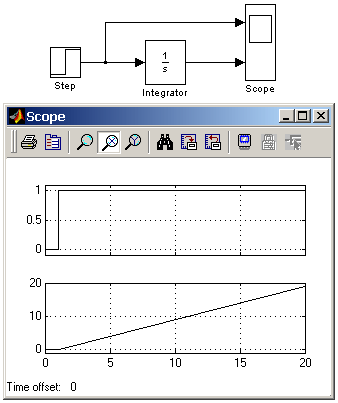 9.4. Discrete – дискретные блоки 9.4.1. Блок единичной дискретной задержки Unit Delay Назначение: Выполняет задержку входного сигнала на один шаг модельного времени. Параметры: Initial condition – Начальное значение для выходного сигнала. Sample time – Шаг модельного времени. Входной сигнал блока может быть как скалярным, так и векторным. При векторном входном сигнале задержка выполняется для каждого элемента вектора. Блок поддерживает работу с комплексными и действительными сигналами. На рис. 9.4.1 показан пример использования блока для задержки дискретного сигнала на один временной шаг, равный 0.1с. 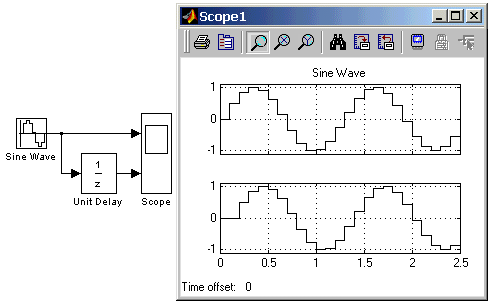 Рис. 9.4.1. Пример использования блока Unit Delay [Скачать пример] 9.4.2. Блок экстраполятора нулевого порядка Zero-Order Hold Назначение: Блок выполняет дискретизацию входного сигнала по времени. Параметры: Sample time – Величина шага дискретизации по времени. Блок фиксирует значение входного сигнала в начале интервала квантования и поддерживает на выходе это значение до окончания интервала квантования. Затем выходной сигнал изменяется скачком до величины входного сигнала на следующем шаге квантования. На рис. 9.4.2 показан пример использования блока Zero-Order Hold для формирования дискретного сигнала. 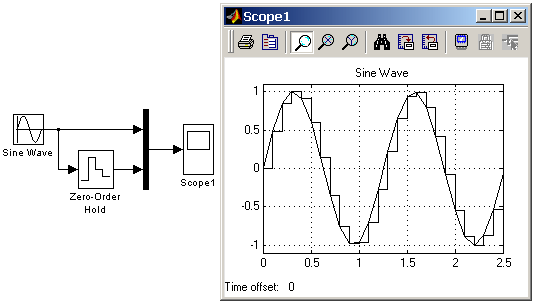 Рис. 9.4.2. Пример формирования дискретного сигнала с помощью блока Zero-Order Hold [Скачать пример] Блок экстраполятора нулевого порядка может использоваться также для согласования работы дискретных блоков имеющих разные интервалы квантования. На рис. 9.4.3 показан пример такого использования блока Zero-Order Hold. Впримере блок Discrete Transfer Fcn имеет параметр Sample time = 0.4 , а для блока Discrete Filter этот же параметр установлен равным 0.8. 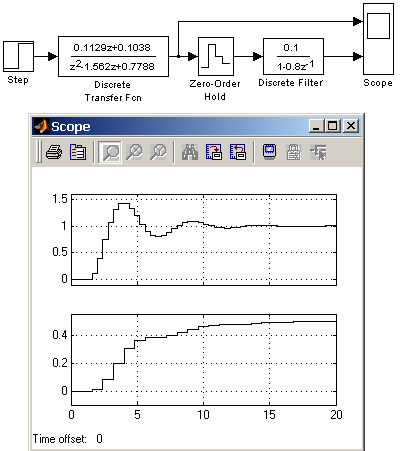 Рис. 9.4.3. Использование блока Zero-Order Hold для согласования работы дискретных блоков. [Скачать пример] 9.4.3. Блок экстраполятора первого порядка First-Order Hold Назначение: Блок задает линейное изменение выходного сигнала на каждом такте дискретизации, в соответствии с крутизной входного сигнала на предыдущем интервале дискретизации. Параметры: Sample time – Величина шага дискретизации по времени. Пример экстраполяции синусоидального сигнала этим блоком показан на рис. 9.4.4. 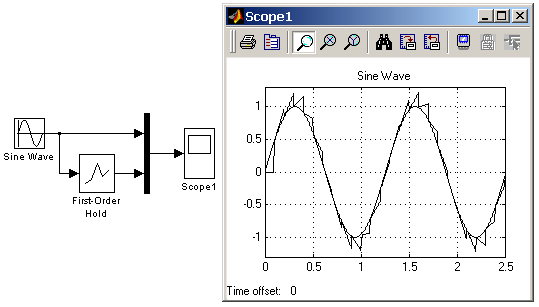 Рис. 9.4.4. Использование блока First-Order Hold [Скачать пример] 9.4.4. Блок дискретного интегратора Discrete-Time Integrator Назначение: Блок используется для выполнения операции интегрирования в дискретных системах. Параметры: Integration method – Метод численного интегрирования: Forward Euler - Прямой метод Эйлера. Метод использует аппроксимацию T/(z-1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: y(k) = y(k–1) + T*u(k–1), y – выходной сигнал интегратора, u – входной сигнал интегратора, T – шаг дискретизации, k – номер шага моделирования. Backward Euler – Обратный метод Эйлера. Метод использует аппроксимацию T*z/(z–1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: y(k) = y(k–1) + T*u(k). Trapeziodal – Метод трапеций. Метод использует аппроксимацию T/2*(z+1)/(z–1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: x(k) = y(k–1) + T/2 * u(k–1). Sample time — Шаг дискретизации по времени. Остальные параметры дискретного интегратора те же, что и у блока аналогового интегратора Integrator (библиотека Continuous). На рис. 9.4.5 показан пример демонстрирующий все три способа численного интегрирования блока Discrete-Time Integrator. Как видно из рисунка изображение блока меняется в зависимости от выбранного метода интегрирования. 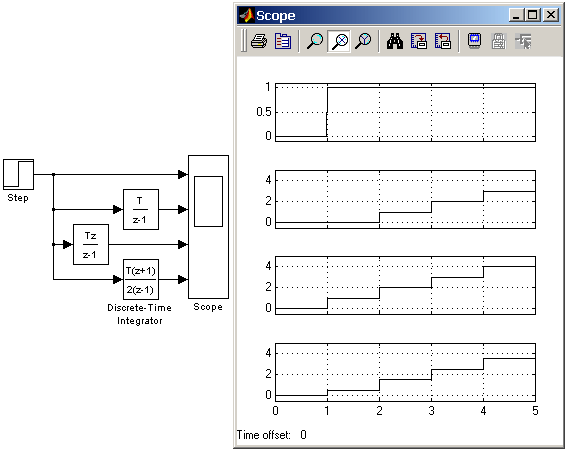 Рис. 9.4.5. Выполнение интегрирования блоками Discrete-Time Integrator, реализующими разные численные методы. [Скачать пример] 9.4.5. Дискретная передаточная функция Discrete Transfer Fсn Назначение: Блок Discrete Transfer Fcn задает дискретную передаточную функцию в виде отношения полиномов: 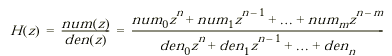 , ,где m+1и n+1 – количество коэффициентов числителя и знаменателя, соответственно. num – вектор или матрица коэффициентов числителя, den – вектор коэффициентов знаменателя. Параметры: |
