ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА. Техническая термодинамика и теплотехника

• Название: Техническая термодинамика и теплотехника
• Дата: 31.05.2022
• Размер: 0.91 Mb.
• Имя файла: ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА.doc
• Тип: Закон; #558647
• страница: 4 из 10

8 Газовые смеси

В качестве рабочего тела тепловых двигателей и установок часто используются смеси различных газов.

Под газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый компонент газовой смеси полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси.

Газовая смесь ИГ подчиняется закону Дальтона – общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих смесь:

(15)

9 Способы задания смеси газов

Газовая смесь может быть задана массовыми, объемными и молярными долями.

Массовой долей ( ) называется отношение массы каждого газа к общей массе смеси:

(16)

Сумма массовых долей всех газов, составляющих смесь, равна единице:

. (17)

Сумма масс всех газов равна массе смеси:

(18)

Объемной долей ( ) называется отношение парциального объема каждого газа к общему объему смеси газов:

. (19)

Сумма объемных долей всех газов, составляющих смесь, равна единице:

. (20)

Сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов:

. (21)

Если молярной долей назвать отношение количества вещества каждого газа n_i к количеству вещества смеси газов , то учитывая, что равно парциальному объему взятого компонента можно написать:

, (22)

где – мольная (молярная) доля i-того газа.

Из выражения (22) следует, что задание смеси молярными долями равнозначно заданию ее объемными долями. Уравнение (22) – соотношение между молярными и объемными долями.

На основании закона Авогадро (при одинаковых условиях молярные объемы любых газов одинаковы) и уравнения Клапейрона – Менделеева существуют следующие зависимости:

или

, (23)

.
Определение кажущейся молекулярной массы и параметров состояния смеси

В теорию газовых смесей введено понятие о средней (кажущейся) молекулярной массе смеси _см, т.е. о молекулярной массе такого воображаемого однородного газа, который по своим свойствам аналогичен рассматриваемой смеси.

Находится кажущаяся молекулярная масса следующим образом. Из определения киломоля вытекает равенство, справедливое для любого однородного газа:

, (24)

где n - количество вещества компонента, моль.

Для смеси по аналогии можно записать:

. (25)

Отсюда, из равенства:

(26)

следует, что: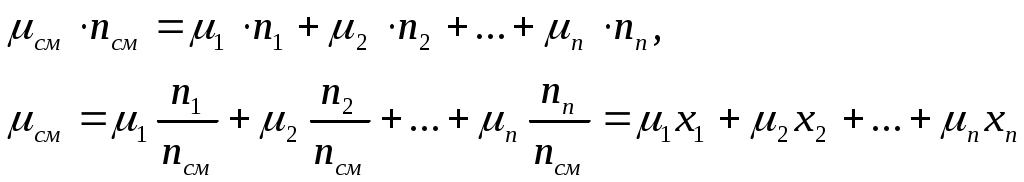

, (27)

где ; ; …; – мольные доли компонентов смеси, моль.

Поскольку то среднюю молекулярную массу можно выразить:

. (28)

Если известен массовый состав смеси, то кажущуюся молекулярную массу смеси вычисляют по уравнению: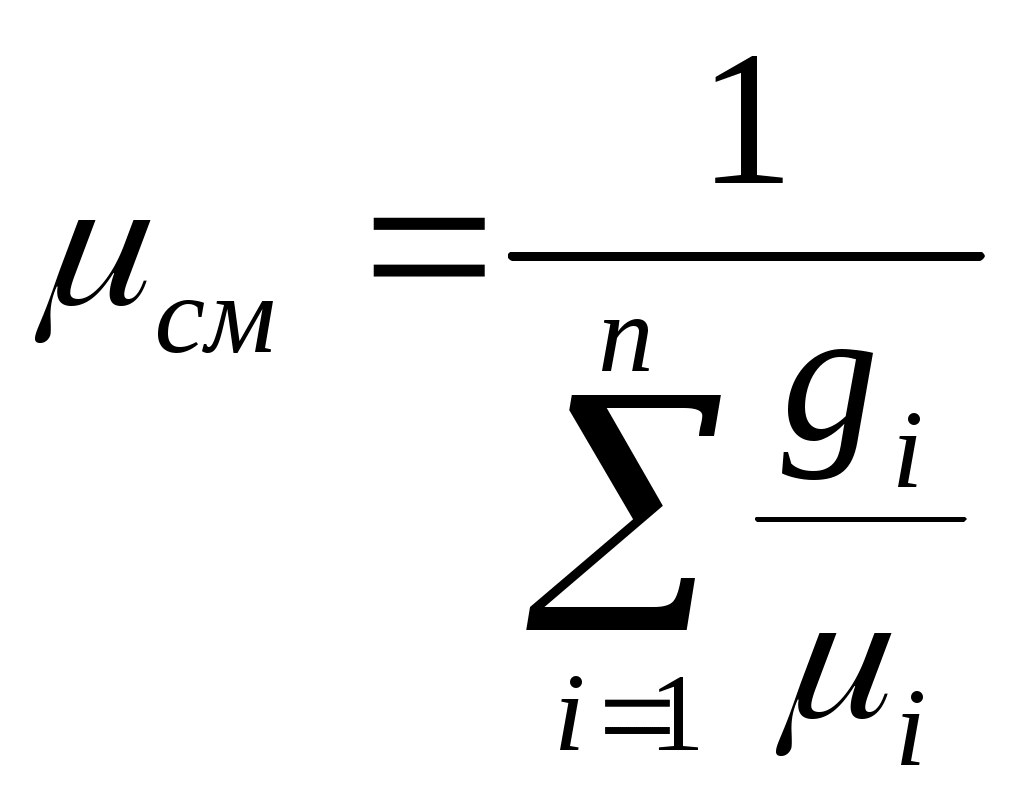

. (29)

Если известен объемный состав смеси (объемная доля компонентов), то плотность смеси газов можно вычислить из соотношений:

. (30)

Если газовая смесь задана массовыми долями, то плотность смеси можно определить из соотношения: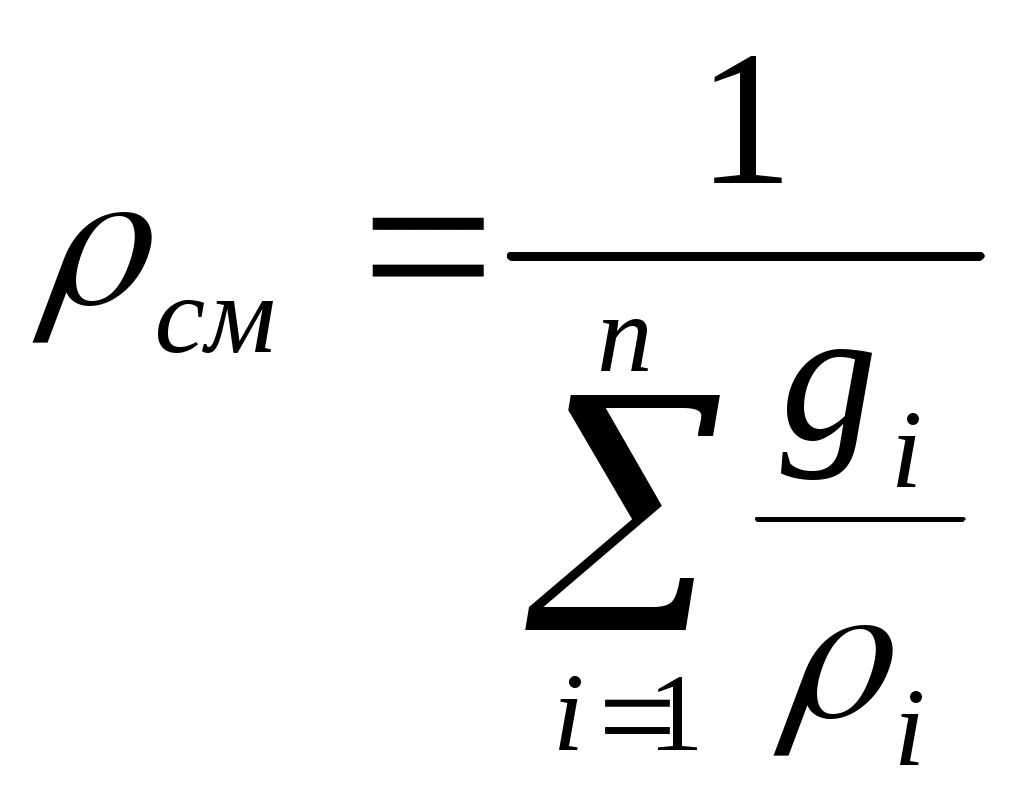

. (31)

Удельный объем смеси представляет величину, обратную плотности смеси: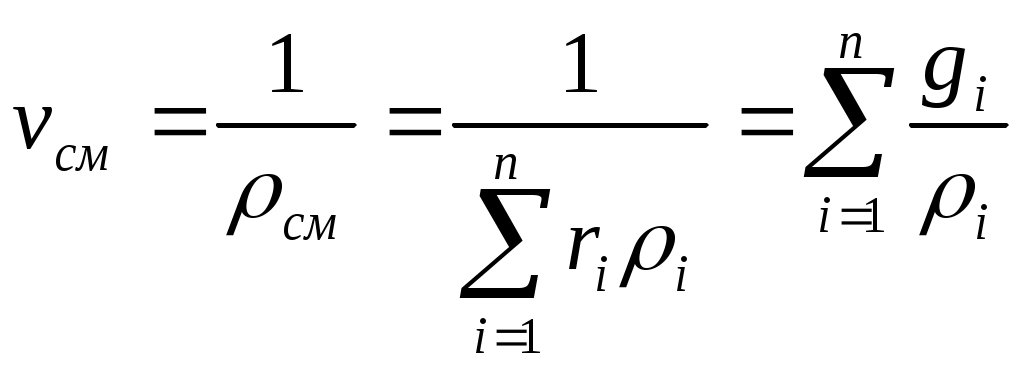

. (32)

Объемные доли компонентов смеси удобно использовать для вычисления парциальных давлений ее составных частей. Из уравнения:

, (33)

следует, что:

, (34)

т.е. для любого компонента смеси можно записать:

. (35)