ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА. Техническая термодинамика и теплотехника

• Название: Техническая термодинамика и теплотехника
• Дата: 31.05.2022
• Размер: 0.91 Mb.
• Имя файла: ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА.doc
• Тип: Закон; #558647
• страница: 8 из 10

16 Аналитическое выражение 2-го закона т-ки

Из выражения (63) термического КПД следует, что

. (73)

Но для обратимого цикла Карно термический КПД еще выражается через температуры источников теплоты:

. (74)

Из сравнения выражений (73) и (74) следует, что для цикла Карно

или .

Но, учитывая, что отводимая теплота отрицательна, имеем:

.

Или

. (75)

Выражение (75) служит для определения приведенной теплоты.

Таким образом, для каждого элементарного цикла Карно справедливо выражение (75), а для всего произвольного цикла:

. (76)

Уравнение (76), выведенное Клаузиусом в 1854 г., представляет собой математическое выражение второго закона термодинамики для произвольного обратимого цикла и называется первым интегралом Клаузиуса.

Если сопоставить уравнение (76) и выражение (60) получим:

. (77)

Выражение (77) показывает, что изменение энтропии замкнутых процессов или циклов равно нолю.

17 ИЗМЕНЕНИЕ ЭНТРОПИИ В НЕОБРАТИМЫХ ПРОЦЕССАХ

При прочих равных условиях работа, совершаемая необратимым процессом, меньше, чем обратимым, и, следовательно, . Поэтому при наличии в цикле необратимых процессов:

, (78)

Или, после интегрирования по замкнутому контуру:

. (79)

Пусть, например, в произвольном цикле, изображенном на рисунке 6, процесс 2-4-1 обратимый, а обозначенный пунктирной линией 1-3-2 необратимый.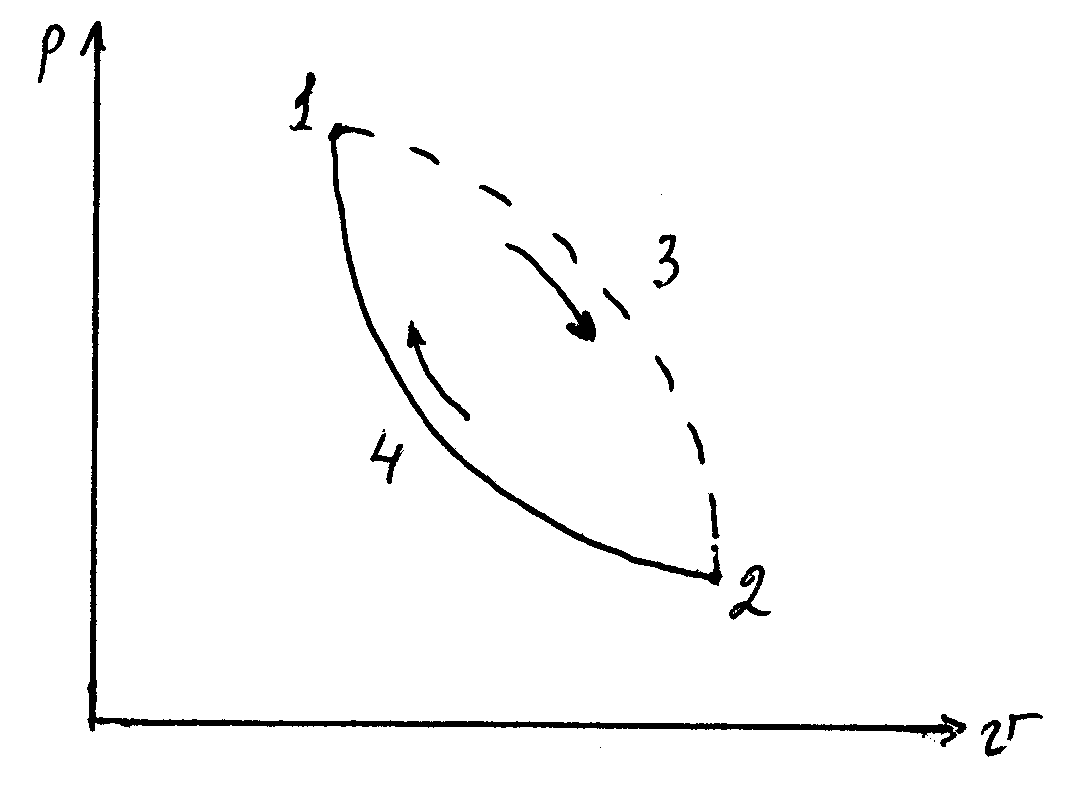



Рисунок 6 – Цикл

Полученный в результате этих процессов цикл будет необратимым, поскольку один из процессов цикла необратим. Тогда интеграл (79) с учетом выражения (78) можно представить в виде суммы интегралов:

. (80)

Так как процесс 2-4-1 обратимый, то второй интеграл, согласно выражению (60), равен разности , поэтому неравенство (80) примет вид:

, (81)

Или, после преобразования:

. (82)

Знак неравенства (82) указывает на то, что в случае необратимого процесса интеграл в правой части его уже не выражает собой разности энтропий, а меньше нее, т.е.

, (83)

где – элементарное изменение энтропии необратимого процесса.

Таким образом, необратимость процесса 1-3-2 приводит к возрастанию энтропии.
18 ЭКСЭРГИЯ
Эксэргия или техническая работоспособность – максимальная работа совершаемая рабочим телом, если в качестве холодного источника теплоты принимается внешняя среда с температурой .

Различают эксэргию рабочего тела в потоке, эксэргию неподвижного рабочего тела и эксэргию теплоты.

Эксэргией рабочего тела, способной в той или иной мере превращаться в работу, является в случае потока энтальпия, а в случае неподвижного тела – внутренняя энергия.

Рассмотрим необратимый процесс передачи тепла Qот горячего тела с температурой к холодному с температурой . Считаем, температуры и выше . В результате этого процесса изменение энтропии первого тела составит:

. (84)

Знак минус указывает на то, что тепло от первого тела отводится, т.е. энтропия убывает.

Тогда, энтропия второго тела возрастает:

. (85)

Суммарное изменение энтропии системы из двух тел: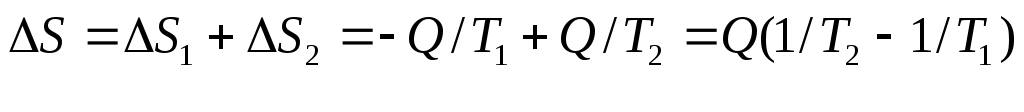

. (86)

Из выражения (86) следует, что энтропия данной системы увеличивается.

Максимальное количество работы за счет тепла Q может быть получено при осуществлении в заданном интервале температур цикла Карно. При этом термический КПД в интервале от до составит:

. (87)

Следовательно, максимальное количество работы будет равно:

. (88)

Максимальное количество работы, которое можно получить от тепла Qпосле необратимого перехода его второму телу, составит:

. (89)

В результате получается, что рассматриваемый необратимый процесс сопровождается уменьшением работоспособности системы на величину:

. (90)

Сравнивая полученное выражение (90) с уравнением (86) получаем выражение:

. (91)

Формула (91) – это уравнение французского физика Гюи-Стодола. Оно вскрывает физический смысл энтропии и показывает, что необратимые процессы перехода тепла с более высокого на более низкий температурный уровень сопровождаются потерей работоспособности, т.е. деградацией энергии той системы, в которой они происходят, а соответствующее возрастание энтропии пропорционально этой потере работоспособности.

Таким образом, энтропию можно рассматривать как параметр замкнутой системы, увеличение которого является количественной мерой потери работоспособности системы, при протекании в ней необратимых процессов.

Понятие об эксэргии тепла позволяет не только осуществить анализ совершенства тепловых устройств, с позиций первого закона термодинамики, но и оценить потерю работоспособности, обусловленную необратимостью происходящих в них процессов, т.е. оценить работу этих устройств и с позиций второго закона термодинамики.
19 ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
При изучении равновесных и обратимых термодинамических процессов идеальных газов должны быть выявлены: во-первых, закономерность изменения основных параметров, характеризующих состояние рабочего тела; во-вторых, особенности реализации условий первого закона термодинамики.

В общем случае два любых параметра рабочего тела могут изменяться произвольно. Однако наибольший интерес представляют частные случаи. К числу частных термодинамических процессов относятся: изохорный, изобарный, изотермический, адиабатный, и политропный, который при определенных условиях может рассматриваться в качестве обобщенного по отношению ко всем выше перечисленным процессам.
Политропный процесс
Политропным процессом называется такой термодинамический процесс изменения состояния физической системы, при котором в течение всего процесса сохраняется постоянство теплоемкости.

Пусть С – теплоемкость политропного процесса, тогда используя выражения 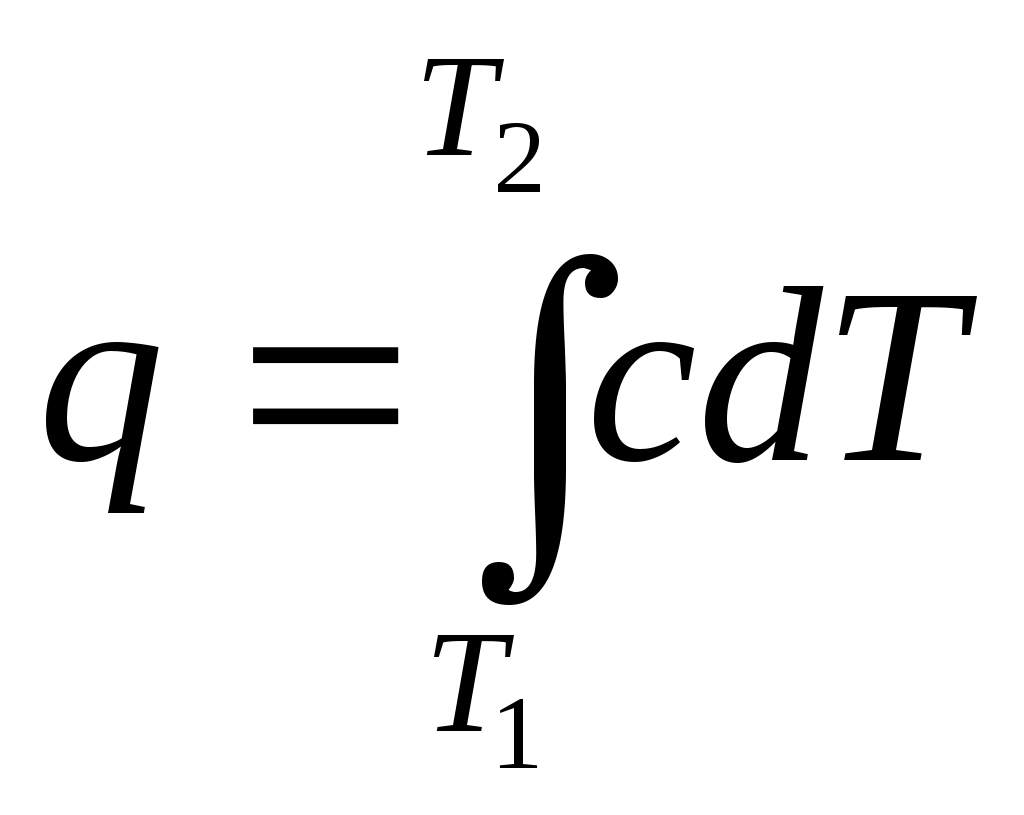или ; и , получим уравнение первого закона термодинамики в виде:

. (92)

С учетом выражения после ряда преобразований имеем:

, (93)

откуда получим уравнение политропы:

, (94)

где – показатель политропы.

Согласно определению политропного процесса n может быть любым, но постоянным в некотором интервале числом, которое достаточно близко воспроизводило бы разнообразные встречающиеся в практике линии индикаторных диаграмм.

Очевидно, что при некоторых частных значениях n уравнение (94) должно превращаться в уравнения простейших термодинамических процессов.

20 Действительно, если в уравнении (94) n= 0, получим уравнение изобары:

.

В этом случае (для изобарного процесса) уравнение первого закона термодинамики для изолированных систем будет совпадать с формулой (49).

При получим уравнение изохоры:

,

поскольку величина будет бесконечно мала по сравнению с объемом ( ), ею можно пренебречь, тогда:

.

22 Из определения изохорного процесса очевидно, что работа в этом процессе не совершается, поскольку работа есть произведение (работа всегда связана с изменением объема). Тогда уравнение первого закона термодинамики для изолированных систем(49) при изохорном процессе примет вид:

. (95)

Таким образом, подведенная к изолированной системе теплота в изохорном процессе расходуется только на изменение внутренней энергии системы.

При получим уравнение изотермы:

,

но поскольку, согласно закону Бойля – Мариотта, если произведение давления и объема есть величина постоянная, то процесс – изотермический, тогда:

.

21 В изотермическом процессе не происходит изменения внутренней энергии системы, поскольку температура постоянна. Тогда уравнение первого закона термодинамики для изолированных систем(49) при изотермическом процессе примет вид:

. (96)

Таким образом, подведенная к изолированной системе теплота в изотермическом процессе расходуется только на совершение системой внешней работы.

При получим уравнение адиабаты:

.

23 Показатель адиабаты еще называют коэффициентом Пуассона. Величина этого показателя зависит от числа атомов в молекуле газа. При этом может принимать следующие значения:

• 
  для одноатомных газов (на самом деле состояние одноатомного газа не существует, оно введено для идеальных газов) ;
  
• 
  для двухатомных газов (CO; О₂; N₂; Н₂; F₂; Cl₂; воздух и др.) ;
  
• 
  для трехатомных газов (CO₂; N₂O; NO₂ и др.) .
  

По определению, адиабатный процесс – это процесс, протекающий без теплообмена с окружающей средой, т.е. . Тогда уравнение первого закона термодинамики для изолированных систем(49) при адиабатном процессе примет вид:

(97)

Таким образом, в адиабатном процессе работа может совершать за счет изменения (уменьшения) внутренней энергии системы в течение некоторого времени.

Таким образом политропный процесс является обобщающим по отношению к простейшим процессам. Для политропы справедливы соотношения: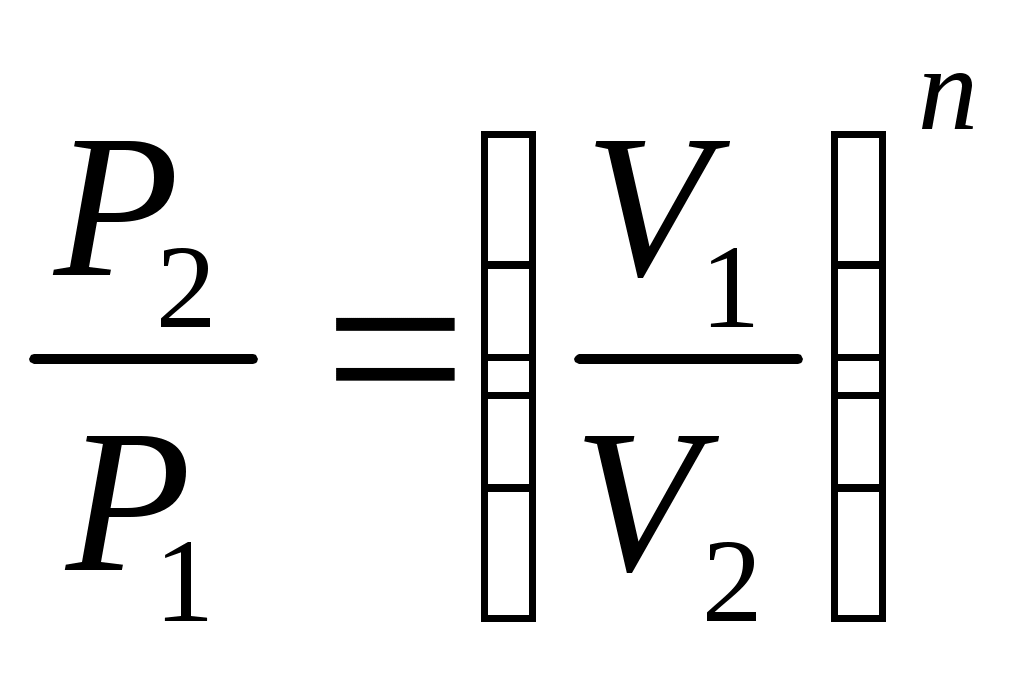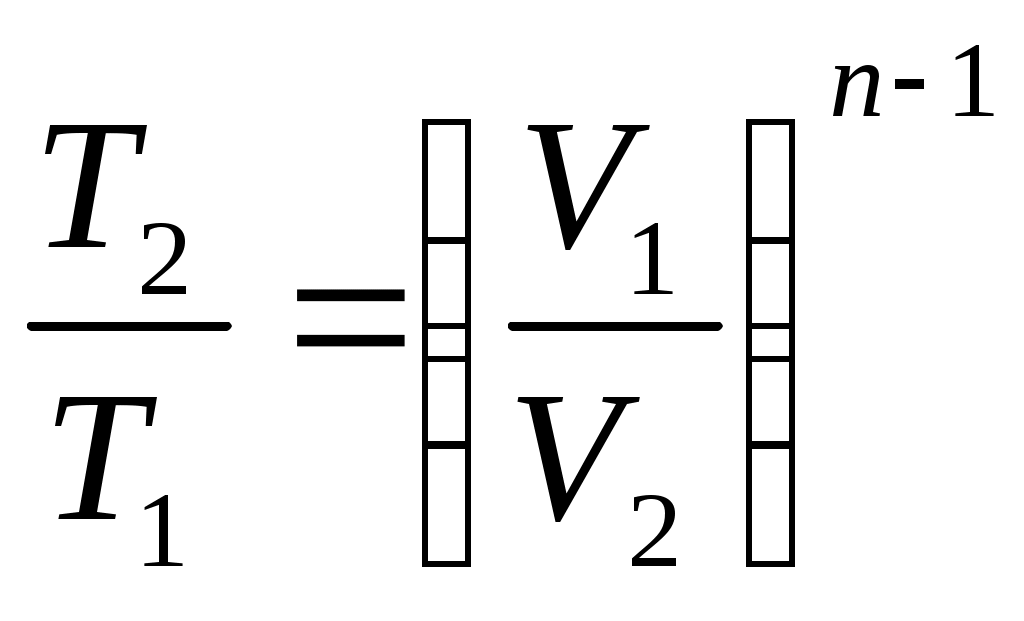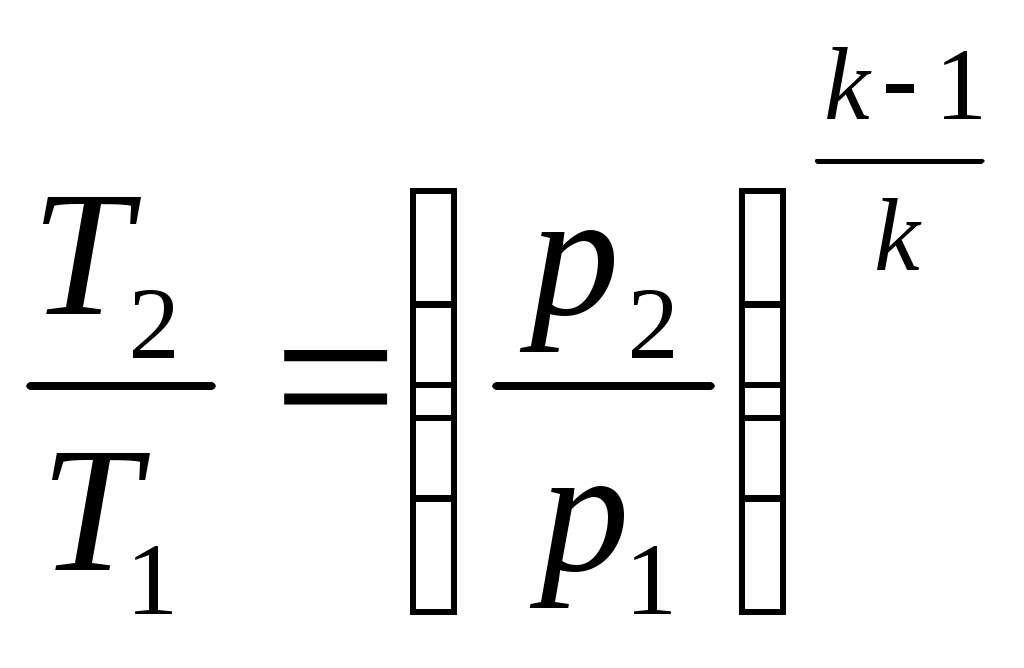

; ; . (98)

Работу политропного процесса можно определить по следующим формулам: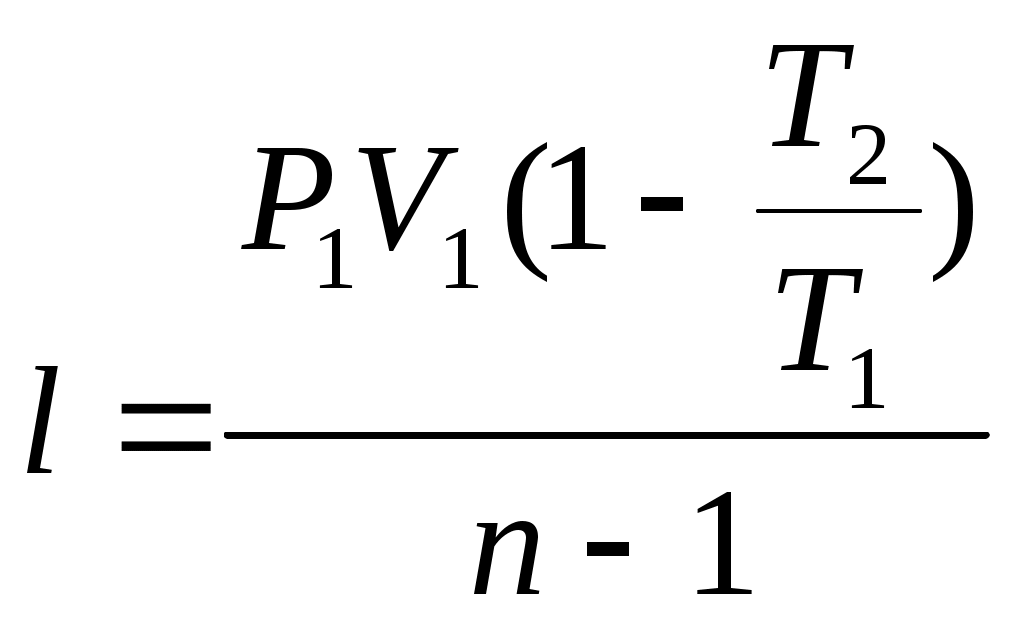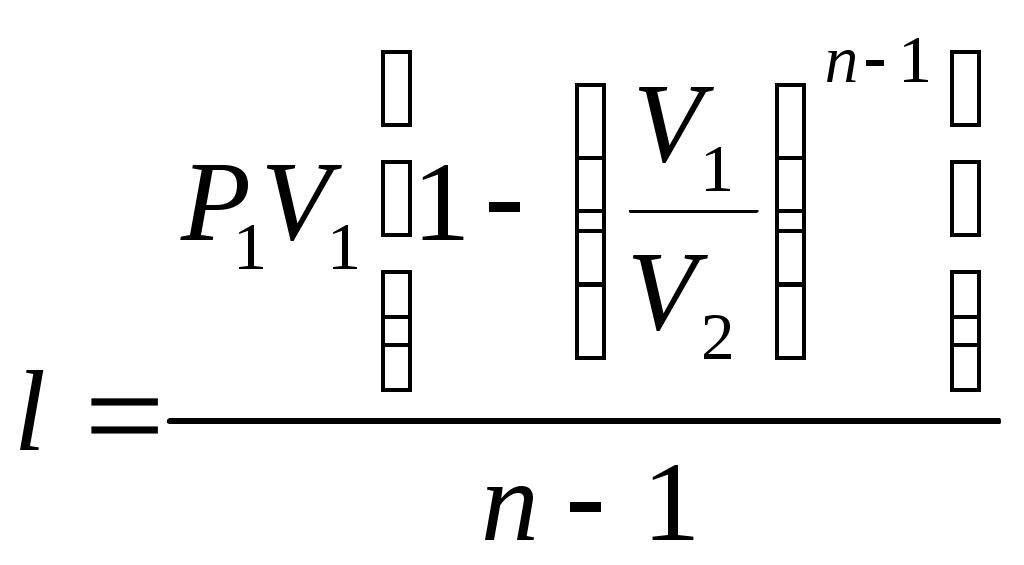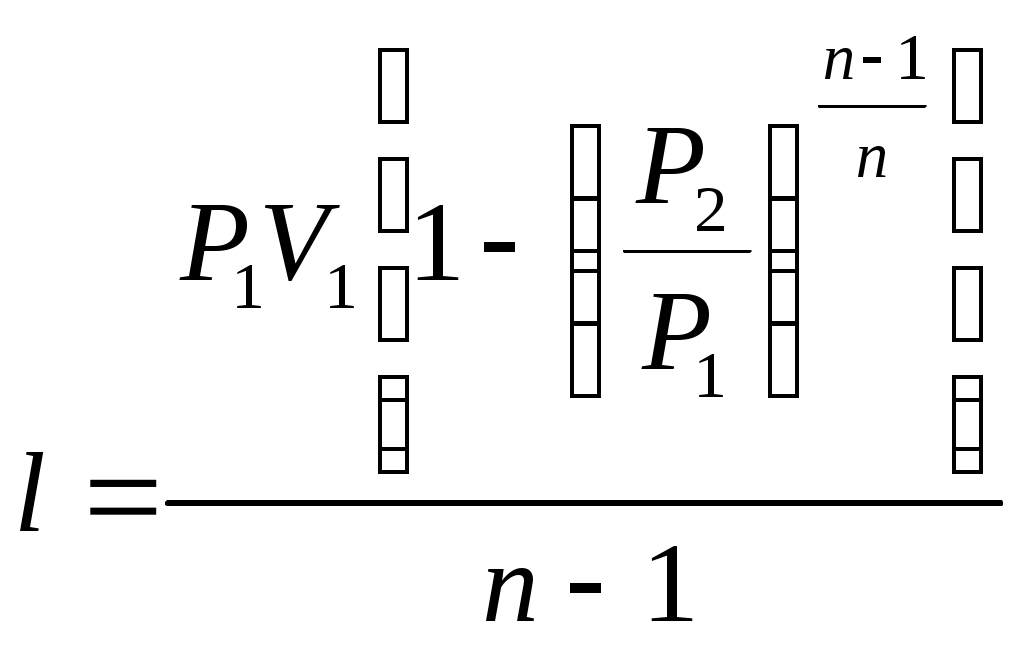

; ; ;

; . (99)
В PV-координатах работа lхарактеризуется площадью под процессом. Если то и верно и обратное.

Теплоемкость политропного процесса можно определить по формуле: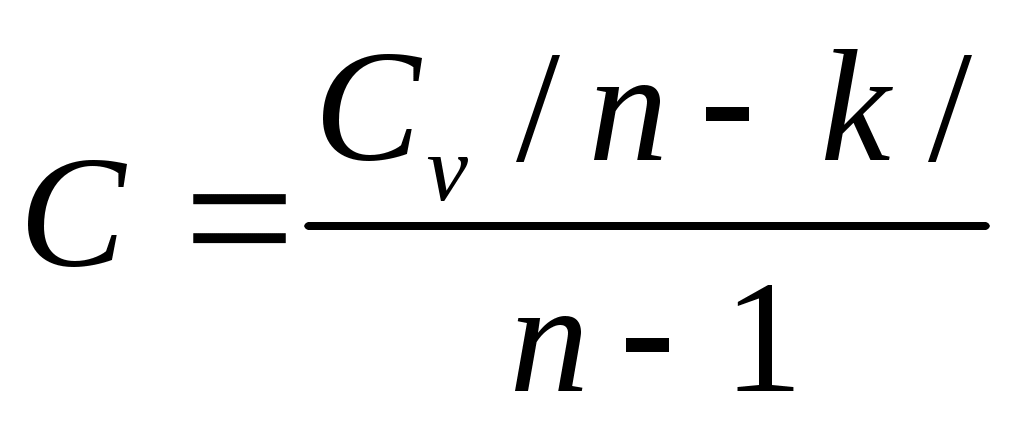

. (100)

Таким образом, еще раз подтверждается, что теплоемкость идеального газа зависит от характера термодинамического процесса, что наглядно подтверждается на рисунке 7.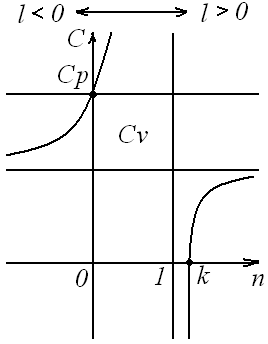



Рисунок 7 – Зависимость теплоемкости С процесса от показателя п политропы

На рисунке 8 представлены совмещенные диаграммы различнох термодинамических процессов.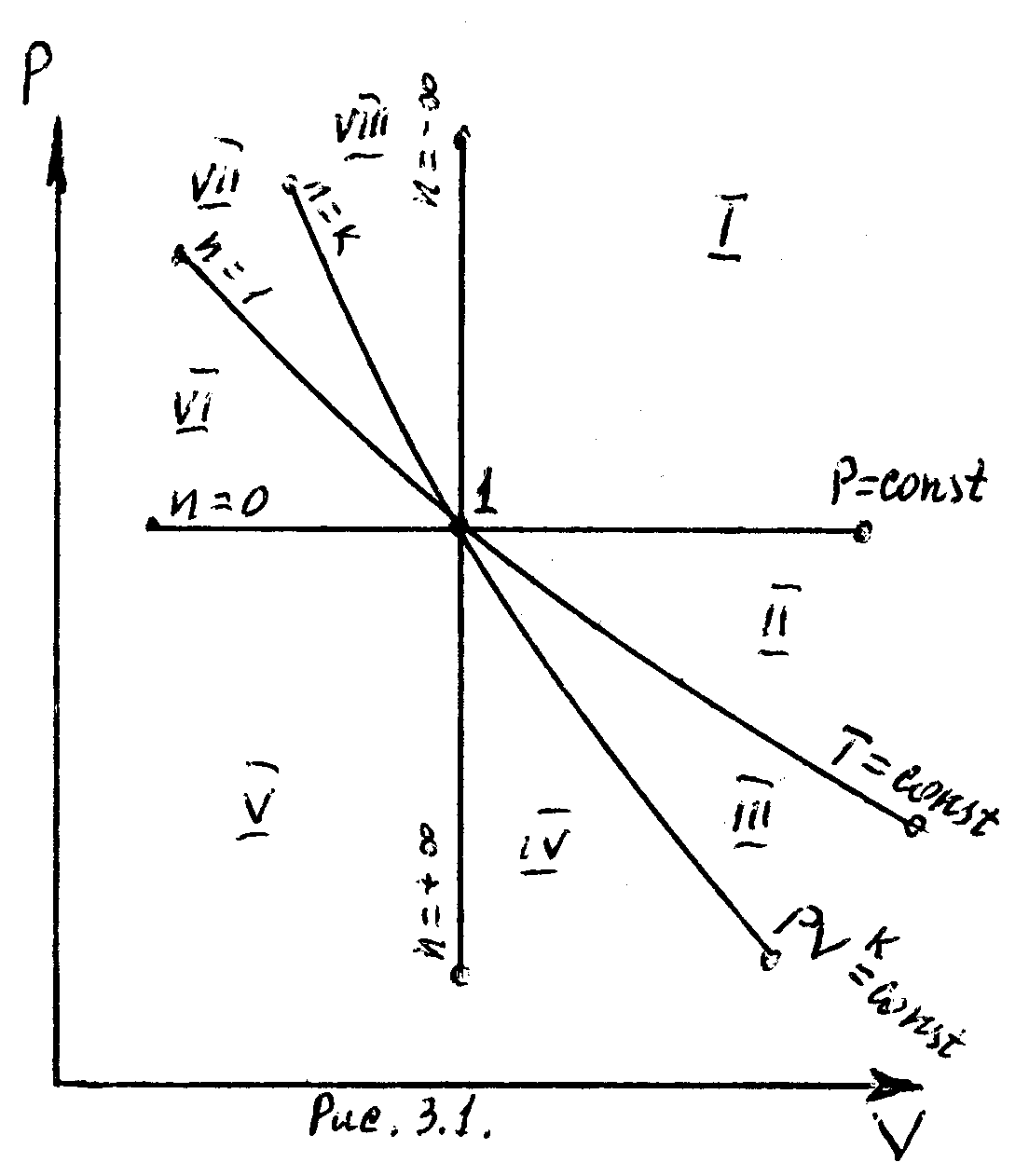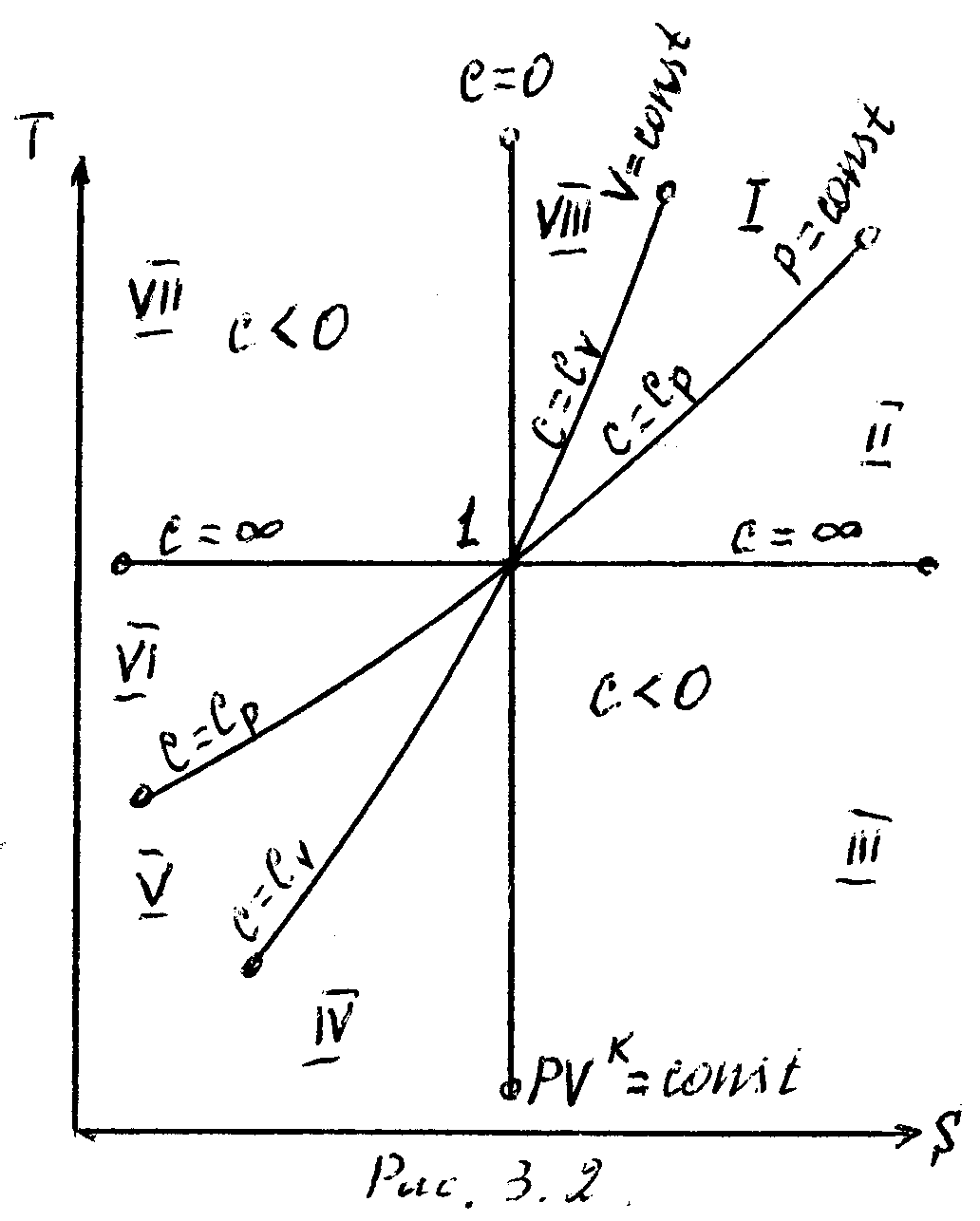

Рисунок 8 - Совмещенные диаграммы различных термодинамических

процессов в PV- и TS – координатах

Если в РV- и ТS – координатах выбрать некоторую произвольную точку 1 и провести из нее все рассмотренные выше термодинамические процессы, то все поле построенной таким образом диаграммы делится на 8 областей, характеризующихся определенными признаками. Так, все процессы слева от точки 1 на РV – диаграмме сопровождаются отрицательной работой. Все процессы справа от точки 1 на TS – диаграмме происходят с подводом теплоты, слева – с отводом теплоты, вверх от изотермы – с увеличением внутренней энергии и энтальпии; вниз – с уменьшением. Области, выделенные на PV – диаграмме, соответствуют процессам с подводом теплоты, а на ТS – диаграмме – процессам с положительной теплоемкостью и т.д.

Для определения изменения энтропии в политропном процессе достаточно уравнение (100) подставить в выражение , и с учетом того, что получим:

. (101)

После интегрирования:

. (102)

С учетом выражений (98), можно записать:

. (103)

Изменения внутренней энергии и энтропии в политропном процессе определяются в ТS – координатах площадями соответственно под изохорным и изобарным процессами, происходящими в том же интервале температур .