ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА. Техническая термодинамика и теплотехника
 Скачать 0.91 Mb.
|
28 Термодинамические процессы в реальных газах и парахСвойства реальных газов Реальные газы отличаются от идеальных газов тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой силами взаимодействия, имеющими электромагнитную и квантовую природу. Эти силы существуют между любыми молекулами при любых условиях и уменьшаются с увеличением расстояния между молекулами. При сближении молекул на малые расстояния силы притяжения резко уменьшаются и переходят в силы отталкивания, достигающие очень больших значений. В связи с этим законы идеальных газов ни при каких условиях не могут быть строго применимы к реальным газам. При практических расчетах различных свойств реальных газов находит широкое применение отношение 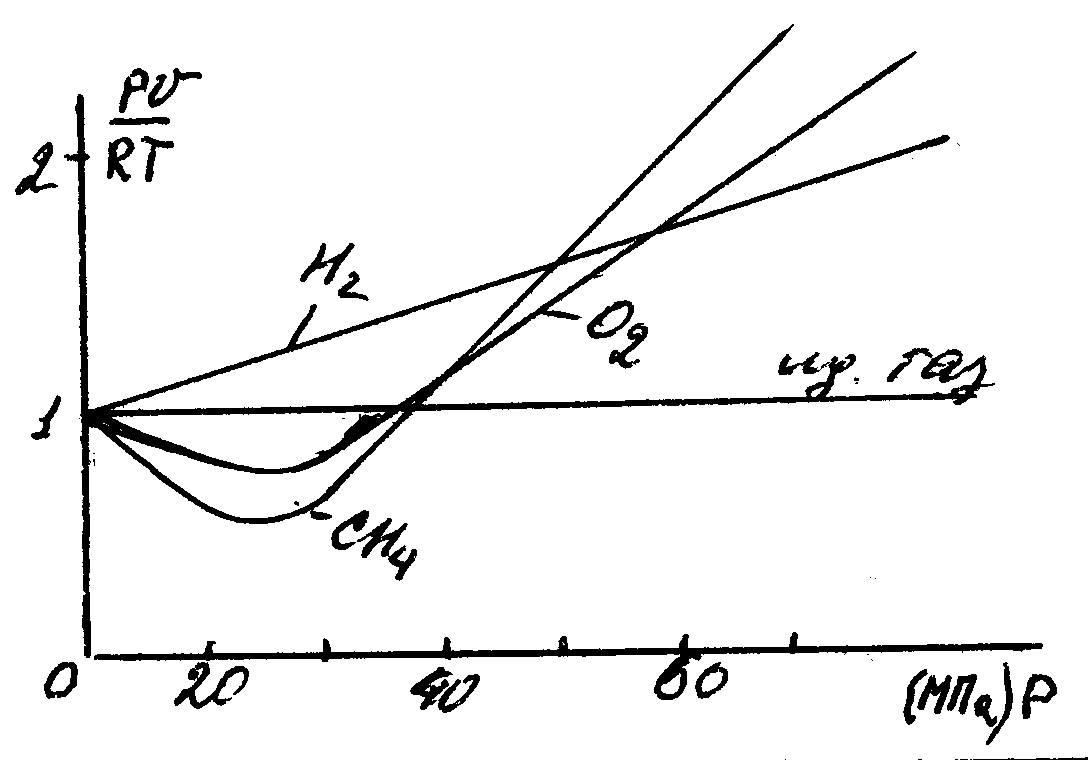 , которое получило название коэффициента сжимаемости. Рисунок 9 – Зависимость коэффициента С от давления Для реальных газов  и в зависимости от давления и температуры может быть больше и меньше 1, и только при очень малых давлениях и высоких температурах оно практически равно 1. Таким образом, свойства реальных газов как в количественном, так и качественном отношениях значительно отличаются от свойств идеальных газов. Поэтому все результаты, полученные для реальных газов на основе законов идеальных газов, нужно рассматривать как приближенные и справедливые при очень больших разрежениях ( ).Отличие свойств любого реального газа от свойств идеального заставило ученых разрабатывать новые уравнения состояния, которые связывали бы значения Р, V, Т и давали бы возможность рассчитывать некоторые свойства газов для разных условий, не прибегая к сложным и дорогостоящим измерениям. За последние 100 лет было предложено значительное число различных уравнений состояния реальных газов, но ни одно из них не решает проблему для общего случая. 29 Развитие кинетической теории газов позволило установить точное уравнение (Боголюбова-Майера) состояния реальных газов в таком виде: 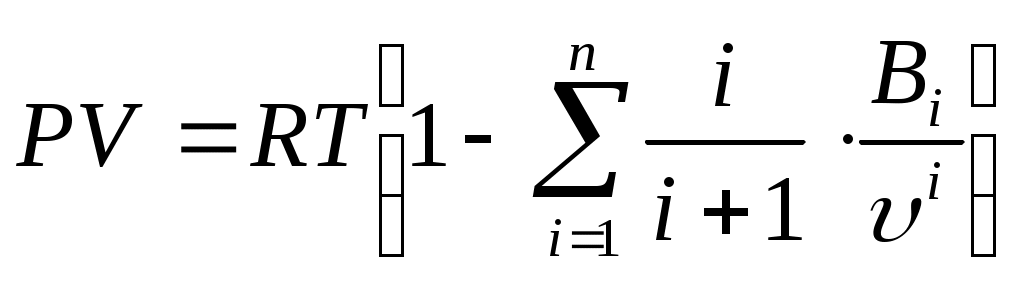 . (104)В этом уравнений коэффициенты  в правой части уравнения называются вириальными коэффициентами и выражаются через потенциальную энергию взаимодействия молекул данного газа и температуру, а  =2, 3, 4 ... – порядковый номер вириального коэффициента.Однако, полученное уравнение в общем виде не может быть использовано для непосредственных расчетов реальных газов из-за сложности вычисления вириальных коэффициентов. 30 Наиболее простым и качественно верно отражающим поведение реального газа является уравнение Ван-дер-Ваальса, которое получается как частный случай из общего уравнения состояния Боголюбова-Майера (104). Если пренебречь в правой части уравнения (104) всеми -тыми членами, содержащими  во 2-ой, 3-ей и т.д. степени, что допустимо, если плотность газа невелика, то получим уравнение Ван-дер-Ваальса, которое было опубликована в 1873 г.:  , (105)где  – поправка на внутреннее давление, определяемое взаимным притяжением молекул газа, для жидкостей оно принимает очень большие значения (например, для H2O при температуре 293 К  1080 МПа, для газов внутреннее давление сравнительно невелико и зависит от Р и Т газа. – поправка на объем самих молекул, т.е. это тот наименьший объем, до которого можно сжать газ.Уравнение Ван-дер-Ваальса (105) при больших плотностях газа дает значительные ошибки, т.к. при его выводе не учитывались некоторые добавочные физические явления, прежде всего так называемые: силовая ассоциация и диссоциация молекул. Кроме того, опытами установлено, что коэффициенты  и  не могут быть постоянными, а должны зависеть от температуры и давления, причем зависимость очень сложная.31 Советские ученые Вукалович М.П. и Новиков И.И. в 1939 г. предложили новое универсальное уравнение состояния реальных газов, качественно отличное от уравнения Ван-дер-Ваальса. При выводе своего уравнения авторы учли указанное выше явление силовой ассоциации молекул под влиянием межмолекулярных сил взаимодействия. В наиболее простой форме, когда учитываются лишь двойные комплексы, уравнение Вукаловича – Новикова имеет следующий вид:  , (106)где а и b – постоянные уравнения Ван-дер-Ваальса; С и m - постоянные, определяемые на основании опытных данных. Полученное Уравнение состояния было взято за основу при создании первых таблиц воды и водяного пара, выпущенных М.П. Вукаловичем в 1940 г. 32 Водяной пар Основные понятия и определения Наибольшее распространение в промышленности получил пар, являющийся рабочим телом в паровых турбинах, в атомных установках, теплоносителем в различных теплообменниках и т. п. Процесс превращения вещества из жидкого состояния в газообразное называется парообразованием. Испарением называется парообразование, которое происходит всегда при любой температуре со свободной поверхности жидкости или твердого тела. Интенсивность испарения возрастает с увеличением температуры жидкости. Процесс кипения заключается в том, что если к жидкости подвести теплоту, то при некоторой температуре, зависящей от физических свойств рабочего тела и давления, наступает процесс парообразования как на свободной поверхности жидкости, так и внутри нее. Переход вещества из газообразного состояния в жидкое или твердое называется конденсацией. Жидкость, полученная при конденсации пара называется конденсатом. Процесс перехода твердого вещества непосредственно в пар называется сублимацией. Обратный переход называется десублимацией. Если парообразование жидкости происходит в неограниченном пространстве, то вся она может превратиться в пар. Если же парообразование протекает в закрытом сосуде, то пар принимает максимальную плотность при данной температуре и называется насыщенным, т.е. это пар, соприкасающийся с жидкостью и находящийся с ней в термическом равновесии. С изменением температуры жидкости равновесие нарушается, вызывая соответствующее изменение плотности и давления насыщенного пара. Насыщенный пар, в котором отсутствуют взвешенные высокодисперсные частицы жидкой фазы, называется сухим насыщенным паром. Состояние сухого насыщенного пара определяется только одним параметром – или давлением, или удельным объемом, или температурой. Насыщенный пар, в котором содержатся взвешенные высокодисперсные частицы жидкой фазы, равномерно распределенные по всей массе сухого насыщенного пара, называется влажным насыщенным паром. Отношение массы сухого насыщенного пара к массе суммарной влажного насыщенного пара называется степенью сухости пара или паросодержанием (  ).Массовая доля кипящей жидкости во влажном паре, равная (  ), называется степенью влажности пара. Для кипящей жидкости при температуре насыщения  , а для сухого насыщенного пара  , следовательно, степень сухости может меняться в пределах от 0 до 1. Таким образом, состояние влажного пара определяется двумя величинами: температурой и давлением или температурой и степенью сухости пара.Если сухому насыщенному пару сообщить некоторое количество теплоты при постоянном давлении, то его температура будет возрастать. Пар, получаемый в этом процессе, называется перегретым. Перегретый пар имеет при данном давлении более высокую температуру и удельный объем, чем сухой насыщенный пар. Перегретый пар над поверхностью жидкости получить нельзя. Температура перегретого пара, так же как и газа, является функцией объема и давления. Перегретый пар является ненасыщенным, так как при данном давлении удельный объем перегретого пара больше удельного объема сухого насыщенного пара, а плотность меньше. Он по своим физическим свойствам приближается к газу и тем ближе, чем выше степень перегрева. 33 PV-диаграмма водяного пара 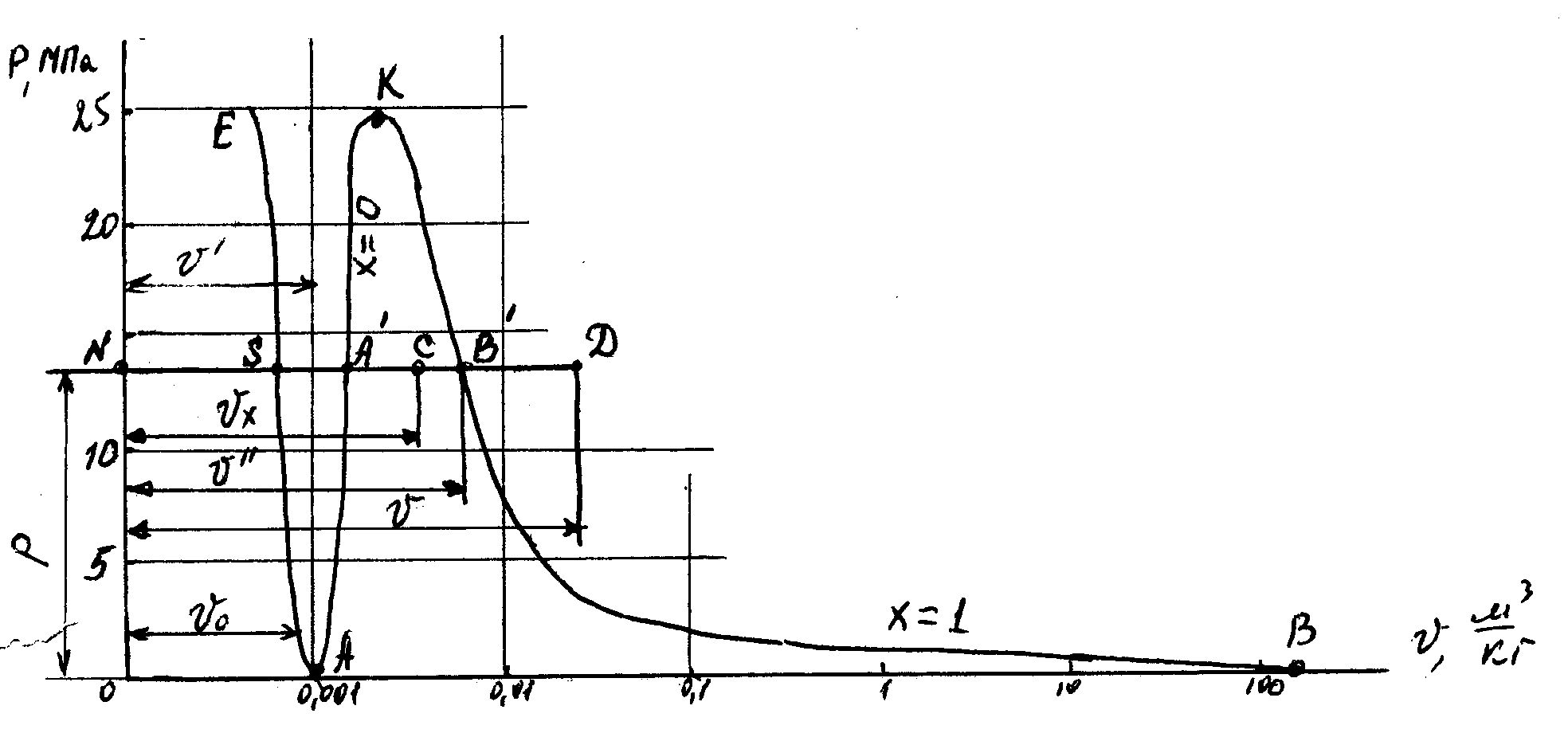 Рисунок 10 – PV-диаграмма водяного пара Фазовая PV-диаграмма системы, состоящей из жидкости фара, представляет собой график зависимости удельных объемов воды и пара от давления. Пусть вода при температуре 0 ºС и некотором давлении занимает удельный объем  (отрезок NS). Вся кривая АЕ выражает зависимость удельного объема воды от давления при температуре 0 ºС. Так как вода – вещество почти несжимаемое, то кривая АЕ почти параллельна оси ординат. Если при постоянном давлении сообщать воде теплоту, то ее температура будет повышаться и удельный объем увеличиваться. При некоторой температуре  вода закипает, а ее удельный объем  в точке  достигает при данном давлении максимального значения. С увеличением давления растет температура кипящей жидкости и также увеличивается.График зависимости от давления представлен кривой АК, которая называется пограничной кривой жидкости. Характеристикой кривой АК является степень сухости .В случае дальнейшего подвода теплоты при постоянном давлении начинается процесс парообразования. При этом количество воды уменьшается, а количество пара увеличивается. В момент окончания парообразования в точке  пар будет сухим насыщенным. Удельный объем сухого насыщенного пара обозначается  .При постоянстве давления температура не изменяется и процесс  является одновременно изобарным и изотермическим. В точках и  вещество находится в однофазном состоянии. В промежуточных точках вещество состоит из смеси воды и пара. Такую смесь называют двухфазной системой.График зависимости удельного объема  от давления представлен кривой  , которая называется пограничной кривой пара, для нее .Точка  соответствует состоянию кипящей жидкости в тройной точке (t 0 ºС), а изобара  соответствует состояниям равновесия всех трех фаз. Эта изобара при выбранном масштабе изображения кривых практически совпадает с осью абсцисс.Если к сухому насыщенному пару подводить теплоту при постоянном давлении, то его температура и объем будут увеличиваться и пар из сухого насыщенного перейдет в перегретый (точка  ).Обе кривые  и  делят диаграмму на три части. Влево от располагается область жидкости, между – двухфазная система, вправо от и вверх от точки  располагается область перегретого пара или газообразного состояния тела. Точка называется критической точкой. Критическая точка является конечной точкой фазового перехода жидкость – пар. Выше точки существование вещества в двухфазном состоянии невозможно. Никаким давлением нельзя перевести газ в жидкое состояние при температурах выше критической.В точке для воды:  = 374,12 ºС;  = 0,003147 м3/кг;  = 22,115 МПа;  = 2095,2 кДж/кг;  = 4,424 кДж/(кгК).При температуре 0 ºС область между линией  и осью ординат – равновесное сосуществование жидкой и твердой фаз. Основные параметры жидкости, сухого и влажного насыщенного пара при 0 ºС и различных давлениях можно приближенно принимать  = 0,001 м3/кг.Удельное количество теплоты, расходуемое на нагревание воды от 0 ºС до температуры кипения при соответствующем давлении, определяется по уравнению:  , (107)где:  – удельная энтальпия кипящей жидкости, Дж/кг; – удельная энтальпия воды при 0 ºС, Дж/кг.В термодинамике удельные энтальпию и энтропию воды в состоянии соответствующем тройной точке, принимают  = 0 кДж/(кгК); = 0 Дж/кг.Удельную внутреннюю энергию воды в этой же точке при 0 ºС также принимают равной нулю. Удельная внутренняя энергия кипящей жидкости определяется из общей формулы, используемой для определения удельной энтальпии:  или  . (108)Энтальпию кипящей жидкости берут из таблиц. Количество теплоты, затраченное на парообразование 1 кг воды при температуре кипения до сухого насыщенного пара, называется удельной теплотой парообразования и обозначается  . С возрастанием давления и температуры уменьшается и в критической точке =0. Удельная теплота парообразования расходуется на изменение внутренней потенциальной энергии или на работу дисгрегации (разъединения) и работу расширения.Удельная энтальпия сухого насыщенного пара определяется по формуле:  , (109)а удельная внутренняя энергия:  . (110)Температура влажного пара равна температуре кипения жидкости при данном давлении. Удельный объем влажного пара  определяется как объем смеси, состоящей из сухого пара и воды: . (111)Удельная энтальпия влажного пара определяется по формуле:  , (112)где  – удельная энтальпия жидкости,  ; – количество теплоты для испарения х-й доли воды.Удельная внутренняя энергия влажного пара:  . (113)Перегретым называют пар, имеющий при данном давлении более высокую температуру, чем сухой насыщенный пар. Удельной теплотой перегрева принято называть то количество теплоты, которое необходимо затратить на перегрев 1 кг сухого пара до требуемой температуры при постоянном давлении. Свойства перегретого пара приближаются к свойствам газа. |