ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА. Техническая термодинамика и теплотехника

• Название: Техническая термодинамика и теплотехника
• Дата: 31.05.2022
• Размер: 0.91 Mb.
• Имя файла: ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА И ТЕПЛОТЕХНИКА.doc
• Тип: Закон; #558647
• страница: 7 из 10

12 ЭНТРОПИЯ

Энтропия (от греческого - поворот, превращение) – понятие впервые введенное в термодинамике немецким физиком Клаузиусом в 1865 г. для определения меры необратимого рассеяния энергии.

Работа, определяемая интегралом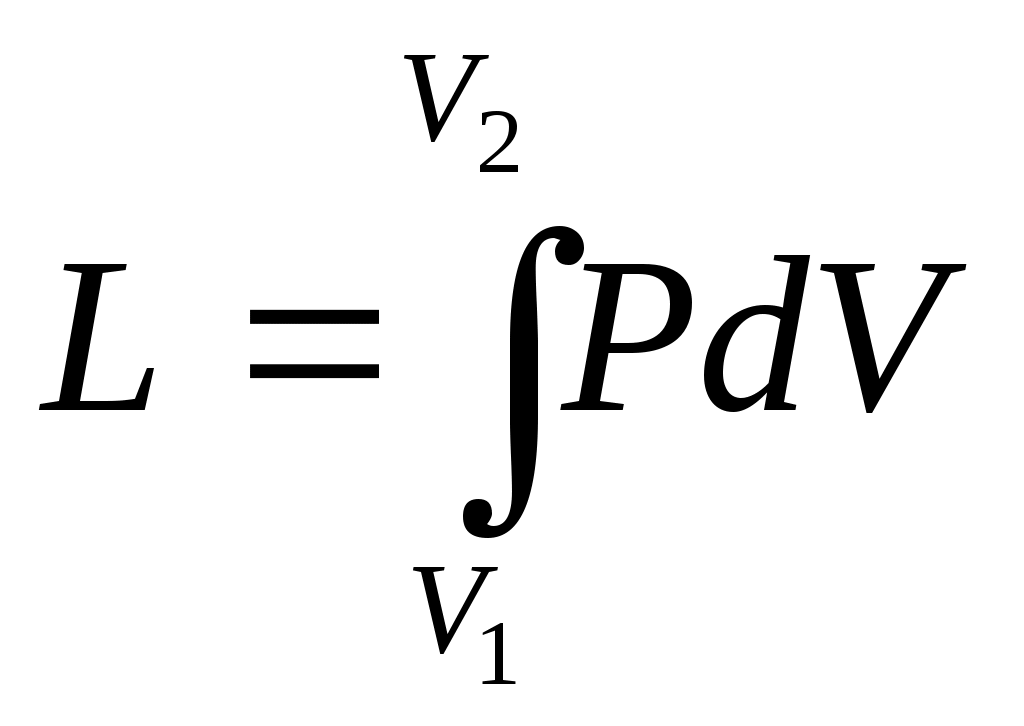

, (59)

совершается рабочим телом в ТДС только тогда, когда изменяется объем. Давление при этом может оставаться постоянным или функционально зависеть от объема. Однако, если Р=0, то и L=0 при любом изменении объема. Работа является одним из видов обмена энергией термодинамической системы с окружающей средой.

Обмен энергией может происходить в виде передачи того или иного количества теплоты q. Значение q как и l, можно подсчитать в виде интеграла, совпадающего по форме с интегралом (59).

Параметр, который изменяется только от количества переданной теплоты и есть энтропия. Энтропия не может быть измерена каким-либо образом, как, например, объем, и определяется только расчетным путем: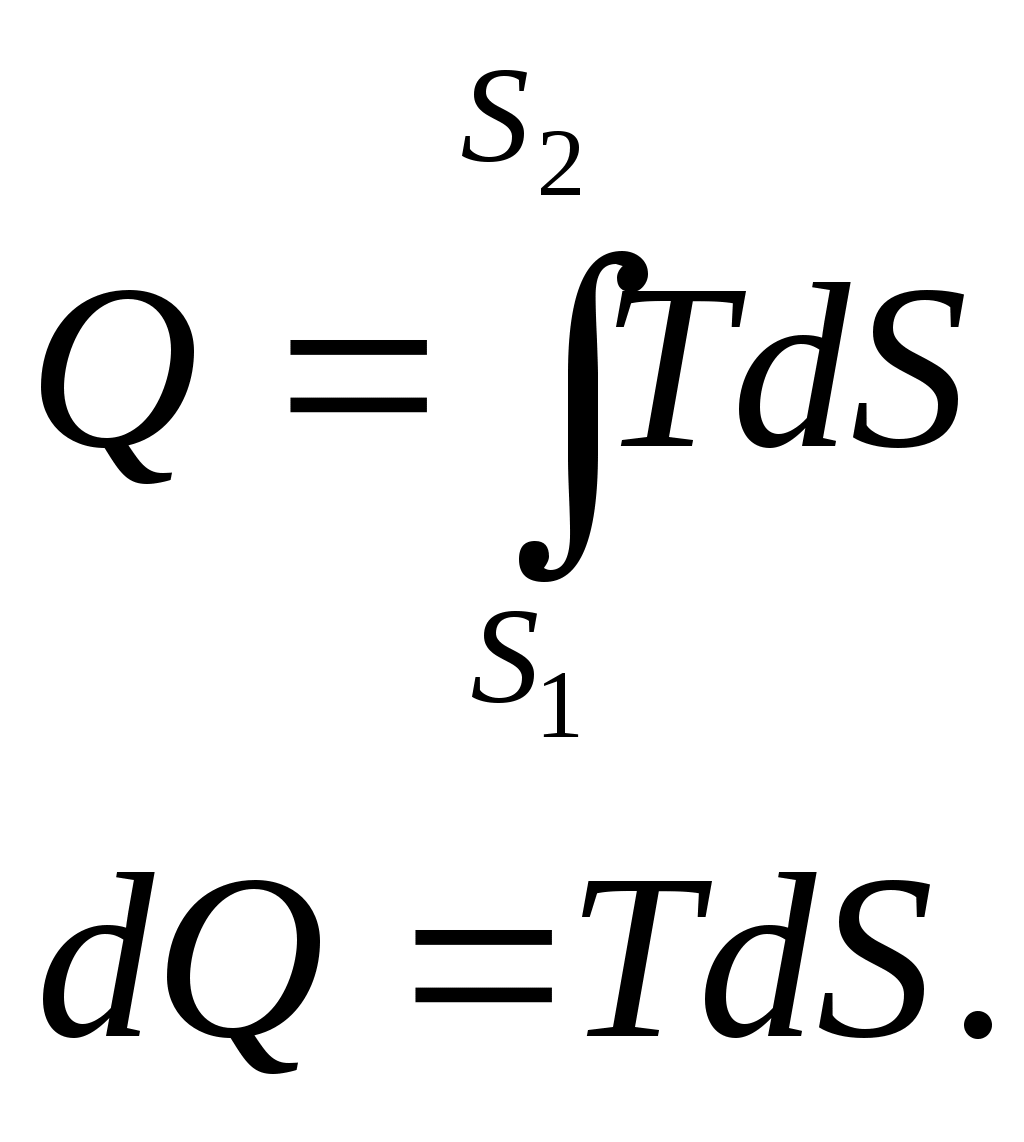

(60)

При теплота подводится, а при отводится.

Для подсчета Q или q через энтропию необходима функциональная зависимость T=f(S) (см. рисунок 4) так же, как при определении количества работы нужна зависимость P=f(V).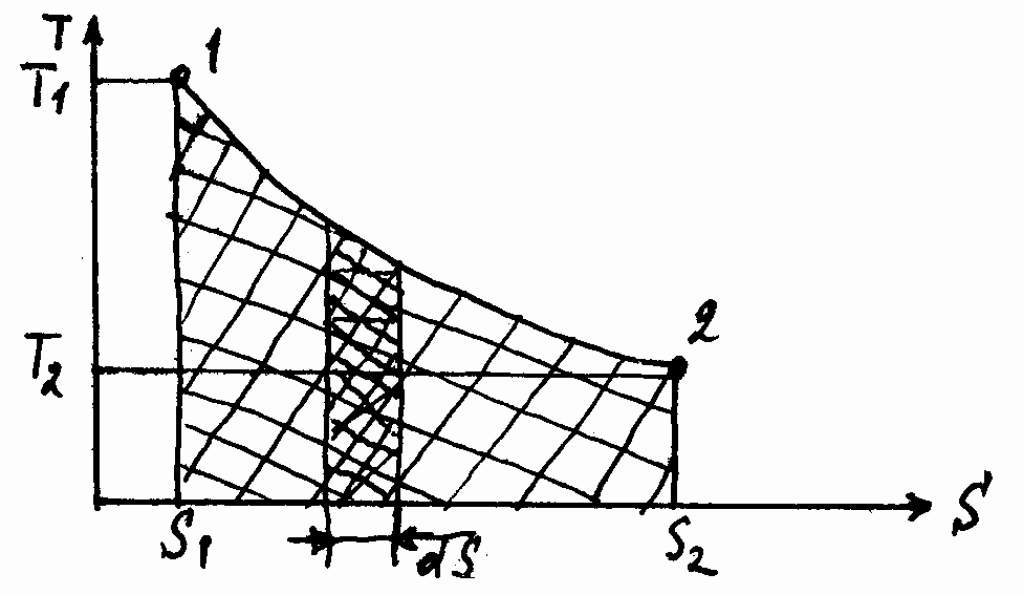



Рисунок 4 – Зависимость энтропии от температуры

В технической термодинамике для расчетов используются не только
PV-координаты (при определении количества работы), характеризующие совершаемую работу, но и TS-координаты (при определении количества теплоты), характеризующие теплообмен с окружающей средой.

13 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

Естественные процессы всегда направлены в сторону достижения системой равновесного состояния. Это явление огранено вторым законом термодинамики, имеющим большое значение для анализа работы теплоэнергетических машин. В соответствии с этим законом, теплота самопроизвольно может переходить только от тела с большей к телу с меньшей температурой, для осуществления обратного процесса должна быть затрачена определенная работа. В связи с этим второй закон термодинамики также можно сформулировать следующим образом: невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более теплым (постулат Клаузиуса 1850 г.)
Второй закон термодинамики определяет также условия, при которых теплота может, как угодно долго преобразовываться в работу.

В любом разомкнутом ТДП при увеличении объема совершается положительная работа, но процесс расширения не может продолжаться бесконечно, и, следовательно, возможность преобразования теплоты в работу ограничена.

Непрерывное преобразование теплоты в работу осуществляется только в круговом процессе или цикле, т.к. каждый элементарный процесс, входящий в цикл, осуществляется при подводе или отводе теплоты dQ,сопровождается совершением или затратой работы dL, увеличением или уменьшением внутренней энергии dU, но всегда при выполнении условия dQ=dU+dL. Интегрирование уравнения (49) первого закона термодинамики для изолированных систем по замкнутому контуру приводит: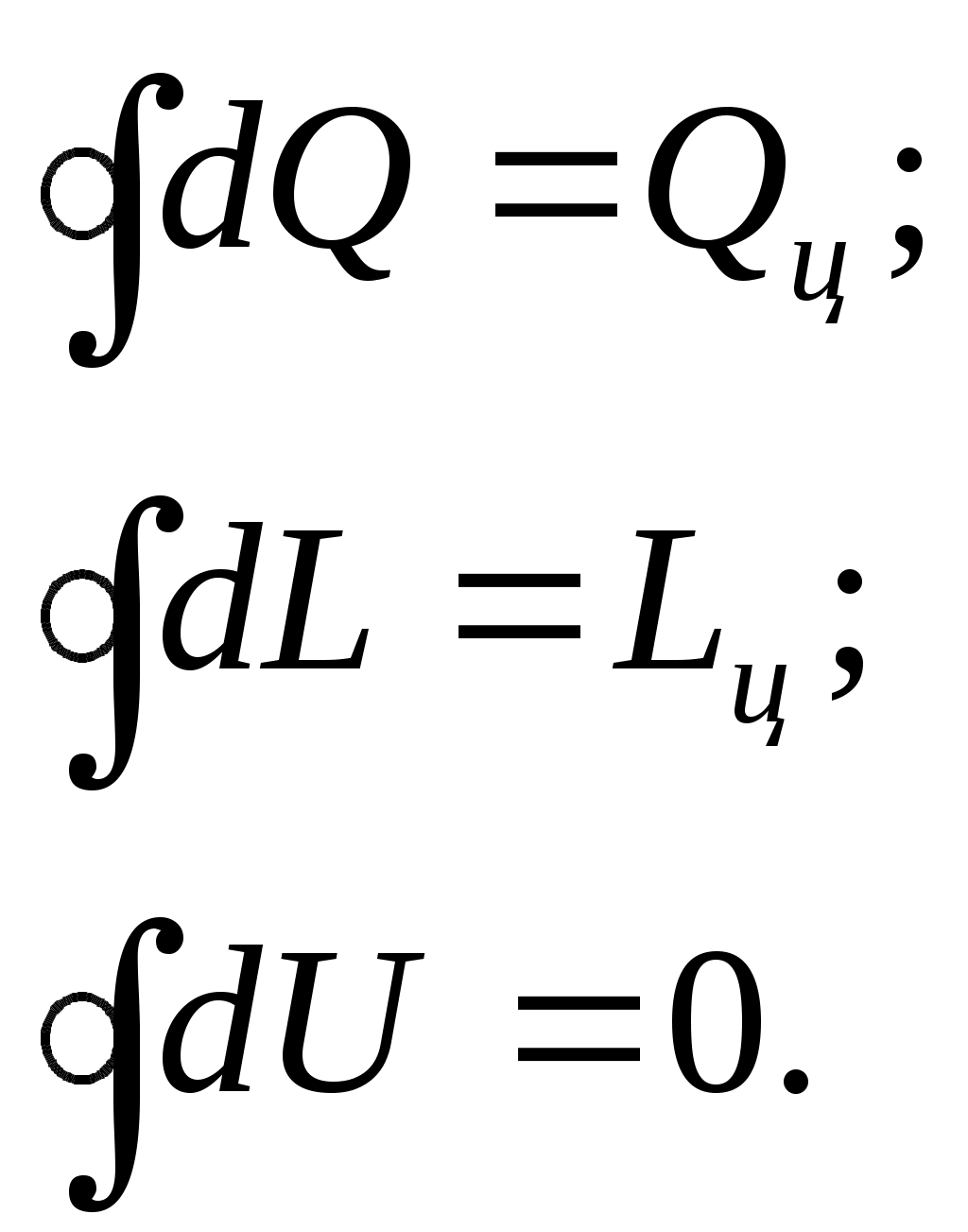

(61)

Работа цикла L_ц представляет собой разность положительных и отрицательных работ элементарных процессов цикла. L_ц определяется площадью, занимаемой циклом.

Элементарное количество теплоты можно рассматривать как подводимое и отводимое от рабочего тела (Q₁ и Q₂). Следовательно,

. (62)

Таким образом, для совершения цикла необходимо иметь два источника теплоты: один с высокой температурой Т₁, а другой – с низкой Т₂. При этом не все затраченное количество теплоты Q₁может быть превращено в работу, т.к. количество теплоты Q₂ передается холодному источнику. В связи с этим второму закону термодинамики были даны еще несколько формулировок:

• 
  передача теплоты от холодного источника теплоты к горячему невозможна без затраты работы;
  
• 
  невозможно построить периодически действующую машину, совершающую механическую работу и соответственно охлаждающую тепловой резервуар (постулат Томсона 1851 г.);
  
• 
  природа стремится к переходу от менее вероятных состояний к более вероятным (постулат Больцмана).
  

14 Термический КПД
Результирующая работа цикла, согласно уравнению (62) определяется разностью работ расширения l₁ и сжатия l₂ так, что l₁ > l₂ и l_ц > 0. Согласно этому утверждению, экономичность работы двигателя тем выше, чем больше работа l_ц, полученная при заданном подводе теплоты .

Тогда термический КПД цикла можно определить:

. (63)

Уравнение (63) справедливо для прямого цикла двигателя, совершающего положительную работу ( ).

Однако существуют и обратные циклы, совершаемые с затратой внешней работы. В обратном цикле за счет затраты внешней работы теплота передается от холодного теплоприемника к горячему. По таким обратным циклам работают холодильные машины. Для оценки экономичности их работы используется холодильный коэффициент:

. (64)
15 Цикл Карно

Изучение идеальных круговых процессов имеет существенное значение для анализа работы теплоэнергетических машин.

Вопрос о том, какая часть тепла, под веденного от горячего источника, может быть превращена в полезную быть превращена в полезную работу в замкнутом процессе, впервые разрешил французский инженер и ученый Сади Карно. Рабочим телом цикла (рисунок 5) служил идеальный газ.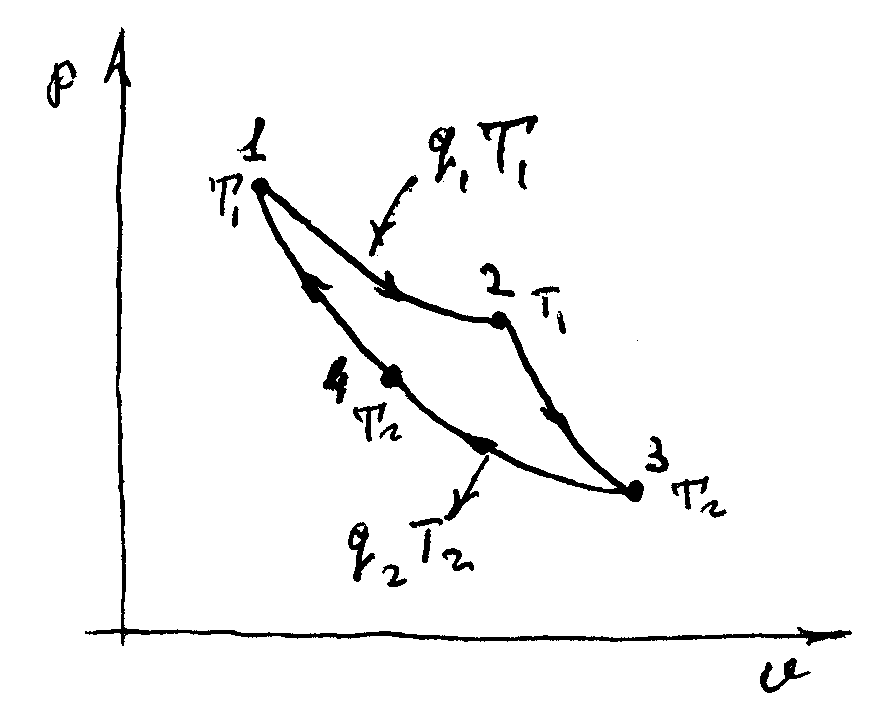



Рисунок 5 – Цикл карно

В этом цикле тепло отводится и подводится по изотермам при температурах горячего источника тепла и холодного теплоприемника.

Произведем анализ прямого цикла Карно (рисунок 5), считая рабочее тело идеальным газом. В этом цикле: процесс 1-2 – изотермическое расширение рабочего тела за счет тепла горячего источника при температуре . Затем рабочее тело отключается от горячего источника и адиабатно расширяется по линии 2-3 с понижением температуры до . После этого рабочее тело подключается к холодному теплоприемнику и сжимается изотермически по линии 3-4, отдавая ему тепло при температуре . Затем оно отключается от теплоприемника и продолжает сжиматься адиабатно по линии 4-1 с повышением температуры до , чем и завершается цикл.

Согласно определению термического КПД для цикла Карно:

, (65)

где (66)

. (67)

Или, учитывая, что под имеется в виду абсолютная величина отводимого тепла, можно записать:

. (68)

Таким образом: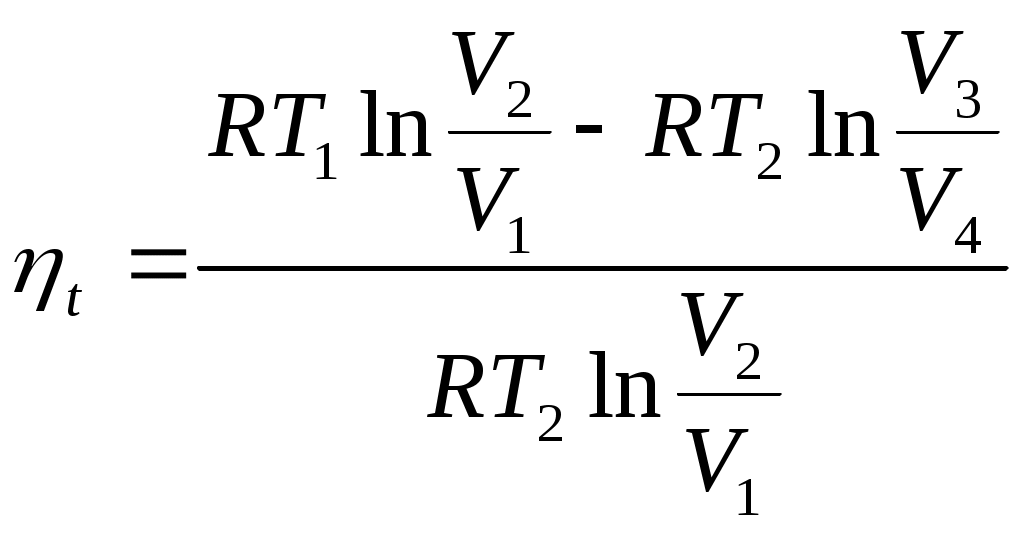

. (69)

Соотношение параметров для адиабаты 2-3 можно записать: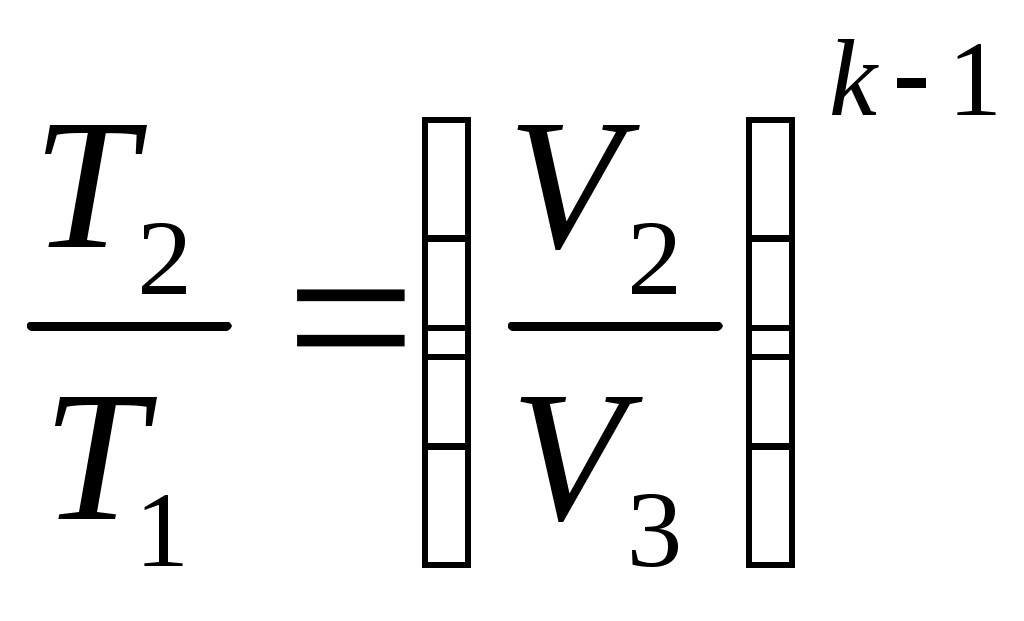

, (70)

а для адиабаты 4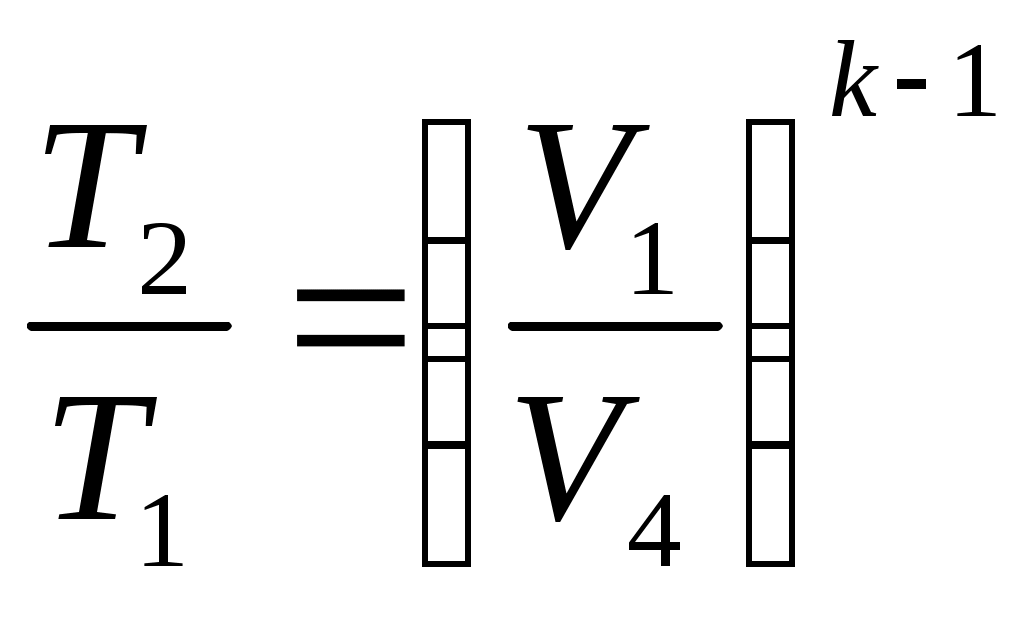-1:

. (71)

Следовательно, и .

Тогда, после сокращения:

. (72)

Полученные выражения показывают, что термический КПД цикла Карно тем больше, чем выше температура горячего источника тепла и чем ниже температура холодного теплоприемника.

В заданном интервале температур цикл Карно является наивыгоднейшим по величине термического КПД, поэтому, хотя цикл Карно в технике и не используется, он играет роль эталона для сопоставления экономичности прямых циклов находящих практическое применение.

Теорема Карно гласит: термический КПД обратимого цикла, осуществляемого между двумя источниками тепла, не зависит от свойств рабочего тела, при помощи которого совершается этот цикл.